Makine Öğreniminde İzotonik Gerileme: Makine Öğreniminde Gerilemeleri Anlama

Doğrusal, lojistik, ridge ve kement regresyonu gibi makine öğrenimi programlarını eğitmek için kullanılan çeşitli regresyon modelleri (algoritmaları) vardır. Bunlardan lineer regresyon modeli en temel ve en yaygın olarak kullanılan regresyon modelidir. Makine öğreniminde izotonik regresyon , doğrusal regresyona dayanır. Bu nedenle, izotonik regresyona geçmeden önce, makine öğrenimindeki lineer regresyona bir göz atalım.

Makine Öğreniminde Doğrusal Regresyonu Anlama

Kaynak

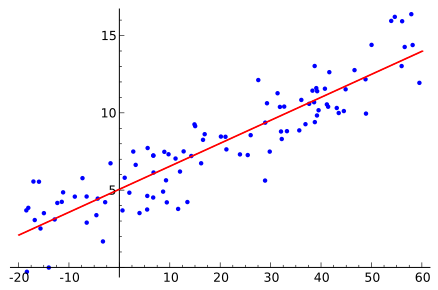
Bağımlı ve bağımsız değişkenler arasındaki ilişkiyi belirlemek için doğrusal regresyon modeli kullanılır. İki değişken arasında en uygun çizgiyle temsil edilen doğrusal bir ilişki olduğunu varsayar. y= mx + c + e denklemi, aşağıdaki durumlarda doğrusal regresyon modelini belirtmek için kullanılır:

m= doğrunun eğimi

c= kesişme

e= modelde hata

Doğrusal regresyon modeli aykırı değerlere karşı hassastır, oldukça esnek değildir ve bu nedenle büyük boyutlu veriler için kullanılamaz. Bu model büyük boyutlu bir test verisine yerleştirildiğinde, çizginin eğiminin dışında kalan ve artık hatalar olarak da adlandırılan birden çok örnek vardır. Çizginin eğiminin dikliğini azaltmak için L1 ve L2 düzenlileştirme gibi yöntemler kullanılabilir, ancak yararlı oldukları kanıtlanmaz.

Mutlaka Okuyun: Makine Öğrenimi Modellerinin Açıklaması

Bu, makine öğrenimi algoritmasının doğruluğunu sınırlar. Bu sınırın üstesinden gelmek için makine öğreniminde yeni bir izotonik regresyon yaklaşımı benimseniyor. Şu anda yaygın olmasa da, bu yaklaşım oldukça güçlüdür ve makine öğrenimi programının doğruluğunu artırmaya yardımcı olabilir.

Makine Öğreniminde İzotonik Regresyonu Anlama

Teknik konulara dalmadan önce, makine öğrenimindeki izotonik regresyonu sıradan olmayan terimlerle anlayalım.

'İzotonik' kelimesinin kodunu çözerek başlayalım. 'İzotonik' kelimesi, 'iso' ve 'tonik' olmak üzere iki kısımdan oluşan Yunanca kök kelimelere sahiptir. Burada 'iso' eşit, 'tonik' ise esneme anlamına gelmektedir. Makine öğrenimi algoritmaları açısından, izotonik regresyon, bu nedenle, lineer regresyon çizgisi boyunca eşit gerilme olarak anlaşılabilir. Doğrusal bir regresyon modelinin üstünde çalışır.

İzotonik regresyonla ilgili, onu daha iyi anlamamıza yardımcı olacak farklı yönlere bir göz atalım.

1. Parçalı Doğrusal Model

Daha önce bahsedildiği gibi, L1 ve L2 düzenlileştirme yöntemlerinin kullanıldığı lineer regresyon çizgisinin eğiminin dikliğinin en aza indirilmesi gerekir. İzotonik regresyon yaklaşımı, grafiği eşikler oluşturarak parçalı bölümlere ayırarak ve uçtan uca bağlı her bölüm için doğrusal bir çizgiye sahip olarak tamamen farklıdır.

Örneğin, yukarıdaki görüntüde, X ekseni, örneğin 10'luk eşit aralıklarla çeşitli daha küçük bölümlere ayrılabilir. Bu aralıkların her biri, bin1, bin2, bin3, bin4 ve benzeri gibi bins olarak adlandırılabilir. üzerinde. Lineer denklem, bu nedenle, şimdi olur,

y= m1x1 + m2x2 + m3x3 +….. mnxn + c, burada:

m1, m2, m3….mn = ayrı kutular için hattın eğimi.

Bu, hatayı en aza indirmeye ve en uygun çizginin eğimini azaltmaya yardımcı olur.

2. Negatif Olmayan Eğim

İzotonik bir fonksiyon monotonik bir fonksiyon olduğundan, çözümün eğimi her zaman negatif değildir. Bir eşikten diğerine geçerken eğimde azalmaya izin verilmez. Bir eşikteki en düşük nokta her zaman bir önceki eşikteki en yüksek noktadan daha büyük olmalıdır.

Örneğin, x1, x2, x3, x4…xn, b1, b2, b3, b4…bn kutularındaki eğim için dikkate alınan veri noktalarının değerleri olsun. Daha sonra, kurala göre, eğim negatif olmamalıdır. Buradan,

f(x1) <= f(x2) <= f(x3) <= f(x4)…<= f(xn).

Bu nedenle, daha düşük bir nokta ile başlıyoruz (burada f(x1) en düşük noktadır) ve her eşik ile kademeli olarak daha yüksek bir noktaya geçiyoruz. Bir eşiğin eğimi sıfır olabilir (yatay çizgi) ama asla negatif olamaz (aşağı eğim).

Okuyun: Yeni Başlayanlar için Makine Öğrenimi Proje Fikirleri

Makine Öğrenimi Modellerinde İzotonik Regresyon Kullanmanın Avantajları

İzotonik regresyonun kullanılması, aşağıda tartışılan iki ana fayda sağlar.

1. Çok Boyutlu Ölçekleme

Birden çok girdi değişkeniniz varsa, izotonik regresyon oldukça yararlıdır. Her bir boyutu her fonksiyon olarak inceleyebilir ve lineer bir şekilde enterpolasyon yapabiliriz. Bu, kolay çok boyutlu ölçeklendirmeye izin verir.

2. Olasılık Değerlerinin Kalibrasyonu

Lojistik regresyonda, bir x değişkenimiz olduğunu ve değişkenin olasılık değerinin artmadığı bir olasılık p(1) belirttiğimizi varsayalım. Ancak gerçekte, gerçek dünyada olasılık değeri daha yüksektir. Bu gibi durumlarda, kalibrasyon amacıyla veya bu tür değişkenlerin olasılığını artırmak için izotonik regresyon oldukça yardımcı olur.

Kontrol edin: Makine Öğrenimi Mülakat Soruları

Makine Öğrenimi Modellerinde İzotonik Regresyon Kullanmanın Dezavantajları

Aşağıda tartışılan izotonik regresyon kullanmanın önemli bir dezavantajı vardır.

Aşırı takma riski

İzotonik kısıtlamaların ve tahmin edici özelliklerin sayısı arttıkça hiperparametrenin (K) fazla takılması riski vardır, ancak sorunu yönetmek için çapraz doğrulama iş akışı yöntemi kullanılabilir.

Çözüm

Şu anda, yalnızca üç ana dilde İzotonik regresyonlu açık kaynaklı paketler bulunmaktadır. Ancak, makine öğrenimi problemlerinde izotonik regresyon kullanmanın faydalarına bakıldığında , gelecekte izotonik regresyon paketlerinin kapsamı, kullanımı ve kullanılabilirliği kesinlikle artacaktır.

İzotonik regresyonun büyük ölçüde lineer regresyon ve L1 ve L2 normalizasyon yöntemlerinin yerini aldığını görebiliriz. Bu nedenle, geleceğe hazır olmak için, şu andan itibaren kendini izotonik regresyon hakkında güncel ve bilgili tutmak gerekir!

Makine öğrenimi veya diğer makine öğrenimi ile ilgili kavramlarda izotonik regresyon hakkında daha fazla bilgi edinmek istiyorsanız , Hindistan'ın en çok satan 4,5 yıldızlı programı olan IIIT-B ve upGrad'ın Makine Öğrenimi ve AI PG Diplomasına göz atabilirsiniz. . Kursta 450+ saat öğrenim, 30'dan fazla vaka çalışması ve ödev bulunur ve öğrencilerin makine öğrenimi ve yapay zeka ile ilgili isteğe bağlı becerileri öğrenmelerine yardımcı olur.