Изотоническая регрессия в машинном обучении: понимание регрессии в машинном обучении

Существуют различные типы регрессионных моделей (алгоритмов), которые используются для обучения программ машинного обучения, например линейная, логистическая, гребенчатая и лассо-регрессия. Из них модель линейной регрессии является самой базовой и наиболее широко используемой моделью регрессии. Изотоническая регрессия в машинном обучении основана на линейной регрессии. Следовательно, прежде чем мы перейдем к изотонической регрессии, давайте сначала рассмотрим линейную регрессию в машинном обучении.

Понимание линейной регрессии в машинном обучении

Источник

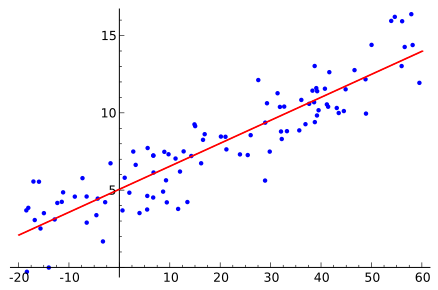
Модель линейной регрессии используется для определения взаимосвязи между зависимыми и независимыми переменными. Он предполагает линейную зависимость, представленную линией наилучшего соответствия между двумя переменными. Уравнение y= mx + c + e используется для обозначения модели линейной регрессии, где:

m = наклон линии

с = перехват

e= ошибка в модели

Модель линейной регрессии восприимчива к выбросам, очень негибкая и, следовательно, не может использоваться для данных большого размера. Когда эта модель развернута на тестовых данных большого размера, есть несколько экземпляров, которые лежат за пределами наклона линии, также называемые остаточными ошибками. Такие методы, как регуляризация L1 и L2, могут использоваться для уменьшения крутизны наклона линии, но они не оказываются столь полезными.

Обязательно прочтите: объяснение моделей машинного обучения

Это ограничивает точность алгоритма машинного обучения. Для преодоления этого ограничения используется новый подход изотонической регрессии в машинном обучении . Хотя в настоящее время этот подход не получил широкого распространения, он очень эффективен и может помочь повысить точность программы машинного обучения.

Понимание изотонической регрессии в машинном обучении

Прежде чем углубляться в технические вопросы, давайте разберемся с изотонической регрессией в машинном обучении с точки зрения непрофессионала.

Начнем с расшифровки слова «изотонический». Слово «изотонический» имеет греческое происхождение и состоит из двух частей: «изо» и «тоник». Здесь «изо» означает равномерный, а «тоник» означает растяжение. Таким образом, с точки зрения алгоритмов машинного обучения изотоническую регрессию можно понимать как равное растяжение вдоль линии линейной регрессии. Он работает поверх модели линейной регрессии.

Давайте рассмотрим различные аспекты, связанные с изотонической регрессией, которые помогут нам лучше понять ее.

1. Кусочно-линейная модель

Как упоминалось ранее, крутизна наклона линии линейной регрессии должна быть минимизирована, для чего используются методы регуляризации L1 и L2. Подход изотонической регрессии полностью отличается тем, что он разделяет график на кусочные участки, создавая пороги и имея линейную линию для каждого участка, соединенного встык.

Например, на приведенном выше изображении ось X можно разделить на различные более мелкие участки, скажем, равными интервалами по 10. Каждый из этих интервалов можно назвать ячейками, например ячейкой 1, ячейкой 2, ячейкой 3, ячейкой 4 и т. д. на. Таким образом, линейное уравнение теперь принимает вид

y= m1x1 + m2x2 + m3x3 +….. mnxn + c, где:

m1, m2, m3….mn = наклон линии для отдельных бинов.

Это помогает свести к минимуму ошибку и уменьшить наклон линии наилучшего соответствия.

2. Неотрицательный наклон

Поскольку изотоническая функция является монотонной функцией, наклон решения всегда неотрицательный. Не допускается уменьшение наклона при переходе от одного порога к другому. Самая низкая точка порога всегда должна быть больше, чем самая высокая точка предыдущего порога.

Например, пусть x1, x2, x3, x4…xn будут значениями точек данных, рассматриваемых для наклона в интервалах b1, b2, b3, b4…bn. Тогда по правилу наклон должен быть неотрицательным. Следовательно,

f(x1) <= f(x2) <= f(x3) <= f(x4)…<= f(xn).

Итак, мы начинаем с более низкой точки (где f(x1) — самая низкая точка) и постепенно продвигаемся к более высокой точке с каждым порогом. Наклон порога может быть нулевым (горизонтальная линия), но никогда не может быть отрицательным (нисходящий наклон).

Читайте: Идеи проекта машинного обучения для начинающих

Преимущества использования изотонической регрессии в моделях машинного обучения

Использование изотонической регрессии дает два основных преимущества, которые обсуждаются ниже.

1. Многомерное масштабирование

Изотоническая регрессия очень полезна, если у вас есть несколько входных переменных. Мы можем проверять каждое измерение как каждую функцию и интерполировать ее линейным способом. Это позволяет легко выполнять многомерное масштабирование.

2. Калибровка значений вероятности

В логистической регрессии предположим, что у нас есть переменная x, и мы обозначаем вероятность p (1), где значение вероятности для переменной не увеличивается. Но на самом деле значение вероятности выше в реальном мире. В таких случаях для целей калибровки или увеличения вероятности таких переменных изотоническая регрессия оказывается очень полезной.

Проверьте: Вопросы для интервью по машинному обучению

Недостатки использования изотонической регрессии в моделях машинного обучения

Существует один существенный недостаток использования изотонической регрессии, который обсуждается ниже.

Риск переобучения

Существует значительный риск переобучения гиперпараметра (K) по мере увеличения количества изотонических ограничений и предикторов, но для решения этой проблемы можно использовать метод рабочего процесса перекрестной проверки.

Заключение

В настоящее время только три основных языка имеют пакеты с открытым исходным кодом с изотонической регрессией. Однако, глядя на преимущества использования изотонической регрессии в задачах машинного обучения , объем, использование и доступность пакетов изотонической регрессии, несомненно, возрастут в будущем.

Мы видим, что изотоническая регрессия в основном заменяет линейную регрессию и методы нормализации L1 и L2. Поэтому, чтобы быть готовым к будущему, необходимо быть в курсе и знать об изотонической регрессии прямо сейчас!

Если вам интересно узнать больше об изотонической регрессии в машинном обучении или других концепциях, связанных с машинным обучением, вы можете ознакомиться с дипломом IIIT-B и upGrad PG по машинному обучению и искусственному интеллекту , который является самой продаваемой программой в Индии с рейтингом 4,5 звезды. . Курс включает более 450 часов обучения, более 30 тематических исследований и заданий и помогает студентам освоить востребованные навыки, связанные с машинным обучением и искусственным интеллектом.