Regresión isotónica en el aprendizaje automático: comprensión de las regresiones en el aprendizaje automático

Hay varios tipos de modelos de regresión (algoritmos) que se utilizan para entrenar programas de aprendizaje automático, como la regresión lineal, logística, de cresta y de lazo. De estos, el modelo de regresión lineal es el modelo de regresión más básico y más utilizado. La regresión isotónica en el aprendizaje automático se basa en la regresión lineal. Por lo tanto, antes de pasar a la regresión isotónica, primero echemos un vistazo a la regresión lineal en el aprendizaje automático.

Comprender la regresión lineal en el aprendizaje automático

Fuente

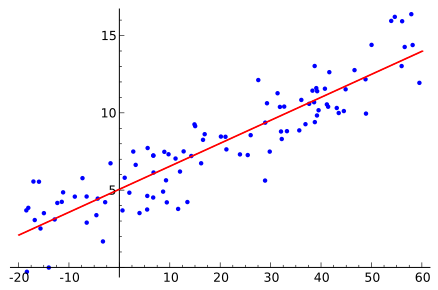
El modelo de regresión lineal se utiliza para determinar la relación entre las variables dependientes e independientes. Supone una relación lineal, representada por la línea de mejor ajuste, entre las dos variables. La ecuación y= mx + c + e se usa para denotar el modelo de regresión lineal donde:

m= pendiente de la recta

c= intersección

e= error en el modelo

El modelo de regresión lineal es susceptible a valores atípicos, es muy inflexible y, por lo tanto, no se puede usar para datos de gran tamaño. Cuando este modelo se implementa en datos de prueba de gran tamaño, hay varias instancias que se encuentran fuera de la pendiente de la línea, también llamadas errores residuales. Se pueden usar métodos como la regularización L1 y L2 para reducir la inclinación de la pendiente de la línea, pero no resultan tan útiles.

Debe leer: Explicación de los modelos de aprendizaje automático

Esto limita la precisión del algoritmo de aprendizaje automático. Se está adoptando un nuevo enfoque de regresión isotónica en el aprendizaje automático para superar este límite. Aunque actualmente no está muy extendido, este enfoque es muy poderoso y puede ayudar a mejorar la precisión del programa de aprendizaje automático.

Comprender la regresión isotónica en el aprendizaje automático

Antes de sumergirnos en los aspectos técnicos, comprendamos la regresión isotónica en el aprendizaje automático en términos sencillos.

Comencemos por decodificar la palabra 'isotónico'. La palabra 'isotónico' tiene orígenes de palabras de raíz griega, compuesta de dos partes, 'iso' y 'tónico'. Aquí, 'iso' significa igual y 'tónico' significa estiramiento. En términos de algoritmos de aprendizaje automático, la regresión isotónica puede, por lo tanto, entenderse como un estiramiento igual a lo largo de la línea de regresión lineal. Funciona sobre un modelo de regresión lineal.

Echemos un vistazo a diferentes aspectos relacionados con la regresión isotónica que nos ayudarán a entenderla mejor.

1. Modelo lineal por partes

Como se mencionó anteriormente, es necesario minimizar la inclinación de la pendiente de la línea de regresión lineal, para lo cual se utilizan los métodos de regularización L1 y L2. El enfoque de regresión isotónica es completamente diferente al dividir el gráfico en secciones por partes al crear umbrales y tener una línea lineal para cada sección conectada de extremo a extremo.

Por ejemplo, en la imagen de arriba, el eje X se puede dividir aún más en varias secciones más pequeñas, digamos en intervalos iguales de 10. Cada uno de estos intervalos se puede llamar bins, como bin1, bin2, bin3, bin4, etc. en. La ecuación lineal, por lo tanto, ahora se convierte en,

y= m1x1 + m2x2 + m3x3 +….. mnxn + c, donde:

m1, m2, m3….mn = pendiente de la línea para bins individuales.

Esto ayuda a minimizar el error y reduce la pendiente de la línea de mejor ajuste.

2. Pendiente no negativa

Dado que una función isotónica es una función monótona, la pendiente de la solución siempre es no negativa. No se permite una disminución de la pendiente al pasar de un umbral a otro. El punto más bajo de un umbral siempre debe ser mayor que el punto más alto del umbral anterior.

Por ejemplo, sean x1, x2, x3, x4…xn los valores de los puntos de datos considerados para la pendiente en los intervalos b1, b2, b3, b4…bn. Entonces, según la regla, la pendiente no debe ser negativa. Por eso,

f(x1) <= f(x2) <= f(x3) <= f(x4)…<= f(xn).

Entonces, comenzamos con un punto más bajo (donde f(x1) es el punto más bajo) y nos movemos gradualmente a un punto más alto con cada umbral. La pendiente de un umbral puede ser cero (línea horizontal) pero nunca puede ser negativa (pendiente descendente).

Leer: Ideas de proyectos de aprendizaje automático para principiantes

Ventajas de usar la regresión isotónica en modelos de aprendizaje automático

El uso de la regresión isotónica ofrece dos beneficios principales, que se analizan a continuación.

1. Escalamiento multidimensional

La regresión isotónica es muy útil si tiene múltiples variables de entrada. Podemos inspeccionar todas y cada una de las dimensiones como todas y cada una de las funciones e interpolarlas de forma lineal. Esto permite un fácil escalado multidimensional.

2. Calibración de Valores de Probabilidad

En la regresión logística, supongamos que tenemos una variable x y denotamos una probabilidad p(1) donde el valor de probabilidad de la variable no aumenta. Pero, en realidad, el valor de probabilidad es mayor en el mundo real. En tales casos, para fines de calibración o aumento de la probabilidad de dichas variables, la regresión isotónica resulta muy útil.

Consulte: Preguntas de la entrevista sobre aprendizaje automático

Desventajas de usar la regresión isotónica en modelos de aprendizaje automático

Hay una desventaja importante de usar la regresión isotónica, que se analiza a continuación.

Riesgo de sobreajuste

Existe un riesgo significativo de sobreajuste del hiperparámetro (K) a medida que aumenta la cantidad de restricciones isotónicas y características predictoras, pero el método de flujo de trabajo de validación cruzada se puede usar para manejar el problema.

Conclusión

Actualmente, solo tres idiomas principales tienen paquetes de código abierto con regresión isotónica. Sin embargo, al observar los beneficios de usar la regresión isotónica en problemas de aprendizaje automático , el alcance, el uso y la disponibilidad de los paquetes de regresión isotónica seguramente aumentarán en el futuro.

Podemos ver que la regresión isotónica reemplaza principalmente a la regresión lineal y los métodos de normalización L1 y L2. Por lo tanto, para estar preparado para el futuro, ¡es necesario mantenerse actualizado y bien informado sobre la regresión isotónica a partir de ahora!

Si está interesado en obtener más información sobre la regresión isotónica en el aprendizaje automático u otros conceptos relacionados con el aprendizaje automático, puede consultar IIIT-B y el Diploma PG de aprendizaje automático e IA de upGrad , que es el programa más vendido de la India con una calificación de 4.5 estrellas. . El curso tiene más de 450 horas de aprendizaje, más de 30 estudios de casos y tareas, y ayuda a los estudiantes a aprender habilidades en demanda relacionadas con el aprendizaje automático y la IA.