機械学習における等張回帰：機械学習における回帰の理解

線形、ロジスティクス、リッジ、ラッソ回帰など、機械学習プログラムのトレーニングに使用されるさまざまなタイプの回帰モデル（アルゴリズム）があります。 これらのうち、線形回帰モデルは最も基本的で最も広く使用されている回帰モデルです。 機械学習の等張回帰は、線形回帰に基づいています。 したがって、等張回帰に進む前に、まず機械学習の線形回帰を見てみましょう。

機械学習における線形回帰の理解

ソース

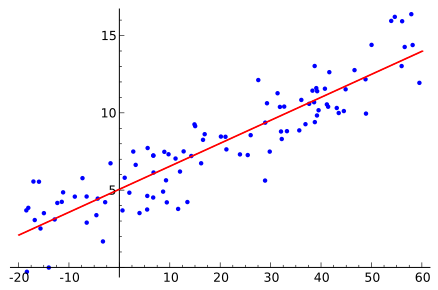
線形回帰モデルは、従属変数と独立変数の間の関係を決定するために使用されます。 これは、2つの変数間の、最適な線で表される線形関係を前提としています。 方程式y=mx + c + eは、線形回帰モデルを表すために使用されます。ここで、

m=線の傾き

c=切片

e=モデルのエラー

線形回帰モデルは、外れ値の影響を受けやすく、柔軟性が非常に低いため、大きなサイズのデータ​​には使用できません。 このモデルを大きなサイズのテストデータに展開すると、線の傾きの外側にある複数のインスタンスが存在します。これは、残差エラーとも呼ばれます。 L1やL2の正則化などの方法を使用して、線の傾斜の急勾配を減らすことができますが、それらはそれほど有用ではありません。

必読：機械学習モデルの説明

これにより、機械学習アルゴリズムの精度が制限されます。 この制限を克服するために、機械学習における等張回帰の新しいアプローチが採用されています。 現在普及していませんが、このアプローチは非常に強力であり、機械学習プログラムの精度を向上させるのに役立ちます。

機械学習における等張回帰を理解する

技術的なことに飛び込む前に、機械学習における等張回帰を素人の言葉で理解しましょう。

「等張」という単語をデコードすることから始めましょう。 「等張」という言葉はギリシャ語の語根であり、「iso」と「tonic」の2つの部分で構成されています。 ここで、「iso」は等しいことを意味し、「tonic」はストレッチを意味します。 したがって、機械学習アルゴリズムの観点から、等張回帰は線形回帰直線に沿った等しいストレッチとして理解できます。 線形回帰モデルの上で機能します。

等張回帰に関連するさまざまな側面を見てみましょう。これは、それをよりよく理解するのに役立ちます。

1.区分的線形モデル

前述のように、線形回帰直線の傾きの急峻さを最小限に抑える必要があり、L1およびL2正則化法が使用されます。 等張回帰アプローチは、しきい値を作成し、エンドツーエンドで接続された各セクションに線形線を設定することにより、グラフを区分的セクションに分割することにより、まったく異なります。

たとえば、上の画像では、X軸をさらにさまざまな小さなセクションに分割できます（たとえば、10の等間隔）。これらの間隔はそれぞれ、bin1、bin2、bin3、bin4などのビンと呼ぶことができます。オン。 したがって、線形方程式は次のようになります。

y = m1x1 + m2x2 +m3x3+…..mnxn+c、ここで：

m1、m2、m3….mn=個々のビンの線の傾き。

これにより、エラーを最小限に抑え、最適な線の傾きを減らすことができます。

2.非負の勾配

等張関数は単調関数であるため、解の傾きは常に負ではありません。 あるしきい値から別のしきい値に移動する場合、勾配を小さくすることはできません。 しきい値の最低点は、常に前のしきい値の最高点よりも大きくする必要があります。

たとえば、x1、x2、x3、x4…xnを、ビンb1、b2、b3、b4…bnの勾配として考慮されるデータポイントの値とします。 次に、原則として、勾配は非負である必要があります。 したがって、

f（x1）<= f（x2）<= f（x3）<= f（x4）…<= f（xn）。

したがって、低いポイント（f（x1）が最低ポイント）から開始し、各しきい値で徐々に高いポイントに移動します。 しきい値の傾きはゼロ（水平線）にすることができますが、負にすることはできません（下向きの傾き）。

読む：初心者のための機械学習プロジェクトのアイデア

機械学習モデルで等張回帰を使用する利点

等張回帰を使用すると、2つの大きな利点があります。これらについては以下で説明します。

1.多次元尺度構成法

複数の入力変数がある場合、等張回帰は非常に役立ちます。 すべての次元をすべての関数として検査し、線形に補間することができます。 これにより、多次元尺度構成法が容易になります。

2.確率値のキャリブレーション

ロジスティック回帰では、変数xがあり、変数の確率値が増加しない確率p（1）を示しているとします。 しかし、実際には、確率値は現実の世界でより高くなります。 このような場合、キャリブレーションの目的またはそのような変数の確率を高めるために、等張回帰が非常に役立つことがわかります。

チェックアウト：機械学習のインタビューの質問

機械学習モデルで等張回帰を使用することのデメリット

等張回帰を使用することの1つの大きな欠点があります。これについては、以下で説明します。

過剰適合のリスク

等張制約と予測子機能の数が増えると、ハイパーパラメーター（K）が過剰適合するという重大なリスクがありますが、交差検定ワークフロー法を使用して問題を管理できます。

結論

現在、3つの主要な言語のみが等張回帰のオープンソースパッケージを持っています。 ただし、機械学習の問題で等張回帰を使用する利点を見ると、等張回帰パッケージの範囲、使用法、および可用性は、将来確実に増加します。

等張回帰が主に線形回帰とL1およびL2正規化方法に取って代わることがわかります。 したがって、将来に備えるためには、これから自分自身を最新の状態に保ち、等張回帰について知識を持っておく必要があります。

機械学習またはその他の機械学習関連の概念における等張回帰について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、インドで最も売れている4.5つ星のプログラムです。 。 このコースには、450時間以上の学習、30以上のケーススタディ、および課題があり、学生が機械学習とAIに関連する需要の高いスキルを学ぶのに役立ちます。