Bayesian vs. Frequentists: อันไหนให้เลือกสำหรับปัญหาต่อไปของคุณ?

หากคุณเคยดูสถิติมาก่อน มีโอกาสที่คุณจะอ่านเกี่ยวกับการโต้วาทีที่ยิ่งใหญ่— Bayesian vs. Frequentists สิ่งเหล่านี้เป็นเพียงแนวทางในการแก้ปัญหาทางสถิติที่เกี่ยวข้องกับความน่าจะเป็น นักสถิติแบบเบย์กล่าวโทษ Frequentists สำหรับวิธีการของพวกเขาและในทางกลับกัน การอภิปรายนี้ไม่มีที่สิ้นสุด ทั้งสองมีข้อดีและข้อเสีย

ในบทความนี้ เราจะพิจารณาทั้งสองวิธีและค้นหาว่าวิธีใดในสองวิธีที่เหมาะกับคุณสำหรับปัญหาทางสถิติครั้งต่อไปของคุณ

Bayesians vs. Frequentists— ในแง่ของความน่าจะเป็น คำจำกัดความ

คำจำกัดความที่ 1: ความน่าจะเป็นในระดับความเชื่อ โดย Frank Ramsey (แนวทางแบบเบย์)

ความน่าจะเป็นของเหตุการณ์วัดจากระดับความเชื่อตามอัตวิสัย เรียกอีกอย่างว่า 'ความน่าจะเป็นเชิงตรรกะ' ซึ่งหมายความว่าคำจำกัดความของความน่าจะเป็นของคุณอาจแตกต่างไปจากของคนอื่น ถ้าเขา/เธอมีหลักฐานมากกว่าคุณ นี่เป็นเรื่องปกติและคนอื่นสามารถคิดอะไรก็ได้ที่เขาต้องการ

คำจำกัดความ 2: ความน่าจะเป็นในระยะยาวโดย Ronald Fisher (Frequentists Approach)

ความน่าจะเป็นของเหตุการณ์เท่ากับความถี่ระยะยาวของเหตุการณ์นั้นเมื่อเกิดซ้ำหลายครั้งซ้ำแล้วซ้ำอีก มีคำตอบสากลอยู่ข้อหนึ่งและไม่เหมือนกับคำจำกัดความที่ 1 ความคิดเห็นต่อความน่าจะเป็นของเหตุการณ์ไม่สามารถเปลี่ยนแปลงไปในแต่ละคนได้ แม้ว่าจะมีหลักฐานมากหรือน้อยก็ตาม

ตัวอย่าง:

สมมุติว่าผมมีเหรียญธรรมดาที่ไม่เอนเอียง มีหัวอยู่ด้านหนึ่งและก้อยอยู่อีกด้านหนึ่ง ตอนนี้ฉันโยนเหรียญ ได้ผลค่ะ แต่คุณในฐานะผู้ชมไม่รู้ว่าเหรียญนั้นขึ้นหรือลง

ผมอยากให้คุณตอบว่า " ความน่าจะเป็นที่เหรียญที่ฉันโยนคือ head-up เป็นเท่า ไหร่?"

จะมีคำตอบที่แตกต่างกันสองประเภทตามคำจำกัดความของความน่าจะเป็นที่แตกต่างกันสอง แบบ

เบย์เซียน

ชาวเบย์จะตอบว่ามีโอกาส 50% ที่เหรียญจะขึ้นหัว คุณในฐานะชาวเบย์จะพูดกับฉันว่า “ คำตอบคือ 50% สำหรับฉัน แต่ใช่ คุณรู้ผลของการโยน ดังนั้น คุณมีโอกาส 100% ที่เหรียญจะออกหัวหรือก้อย แต่คุณรู้อะไรไหม ฉันไม่สนใจ เพราะตามแหล่งข้อมูลที่มีให้ฉัน คำตอบคือ 50% สำหรับฉัน ”

frequentists

ผู้ที่ใช้บ่อยจะตอบคำถามว่า " มีโอกาส 100% หรือโอกาส 0% ที่เหรียญจะขึ้นหัว เนื่องจากเหรียญได้รับการลงจอดแล้ว จึงไม่มีประโยชน์ใดในการผูกความน่าจะเป็นกับค่าคงที่และค่าคงที่นี้ ผลของการโยนถือเป็นที่สิ้นสุดและจะไม่มีการเปลี่ยนแปลงใดๆ จะไม่มีการเปลี่ยนแปลงของคำตอบในหมู่ใคร

อ่าน: ประเภทของการเรียนรู้ภายใต้การดูแล

Bayesian vs. Frequentists— ในแง่ของการใช้ความน่าจะเป็นก่อนหน้า

ให้เราดูตัวอย่างอื่น

เราจะนำตัวอย่างข้างต้นไปอีกขั้น ฉันจะโยนเหรียญหลายครั้ง สมมติว่า 14 ครั้ง คุณได้จดบันทึกผลการโยนเหรียญ 14 ครั้งที่ผ่านมา ตอนนี้เป็นครั้งที่ 15 ที่ฉันโยนเหรียญอีกครั้ง ตอนนี้คุณจะถูกถามว่า " ความน่าจะเป็นที่เหรียญที่โยนนี้ขึ้นหัวเป็น เท่าไหร่ "

เบย์เซียน

หากคุณเป็น Bayesian สิ่งที่คุณจะใช้คือคำที่รู้จักกัน ก่อนหน้า นี้ ให้เราพิจารณาสูตรของ Bayes สำหรับความน่าจะเป็นแบบมีเงื่อนไข:

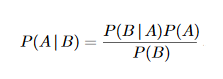
โดยที่ A และ B เป็นเหตุการณ์บางอย่าง และ P(A | B) ถูกกำหนดให้เป็นความน่าจะเป็นของเหตุการณ์ A ที่กำหนด เหตุการณ์ B ได้เกิดขึ้นแล้ว

ตอนนี้ คำว่า P(A) ถูกกำหนดไว้ก่อนหน้านี้ ซึ่งถูกกำหนดให้เป็นความน่าจะเป็นที่เหตุการณ์ A เป็นจริงก่อนที่จะพิจารณาข้อมูล

กลับมาที่ตัวอย่าง ในฐานะ Bayesian คุณจะใช้คำก่อนหน้า นั่นคือ คุณจะตัดสินใจโดยอิงจากผลการโยนเหรียญในอดีต

สมมุติจากการโยนเหรียญ 14 ครั้ง ผมได้หัว 9 ครั้ง คุณอาจพูดว่า "ฉันมีโอกาสสูงที่จะได้หัว" ไม่เพียงแต่คุณพูดอย่างนั้น แต่การคำนวณของคุณจะสนับสนุนข้อโต้แย้งของคุณด้วย ดังนั้นการตัดสินใจของคุณจึงเปลี่ยนแปลงไปเนื่องจากผลลัพธ์ 'ก่อนหน้า' ความสามารถในการตัดสินใจขึ้นอยู่กับระดับของความเชื่อในการเลือกก่อน การกำหนดความน่าจะเป็นก่อนหน้านี้เป็นหนึ่งในปัจจัยสำคัญในผลลัพธ์ของ Bayesian

ต้องอ่าน: ประเภทของแบบจำลองการถดถอยในการเรียนรู้ของเครื่อง

frequentists

หากคุณเป็นคนบ่อย คุณจะไม่เห็นด้วยอย่างยิ่งกับสิ่งที่ Bayesian พูด คุณไม่มีความสนใจในสิ่งก่อนหน้าใด ๆ เนื่องจากค่าก่อนหน้ามักจะเป็นค่าที่คาดเดาได้ แนวคิดของคุณขึ้นอยู่กับการประมาณการความเป็นไปได้สูงสุด สิ่งที่คุณจะทำคือ คุณจะรวบรวมข้อมูลตัวอย่างจากประชากร ตอนนี้ประเมินค่ากลางซึ่งส่วนใหญ่เหมือนกันกับค่าเฉลี่ยของข้อมูล ค่านี้คือจุดที่เป็นไปได้สูงสุด (ค่าประมาณ) ของพารามิเตอร์ที่ไม่แน่นอน

นักเล่นประจำอาจสันนิษฐานได้ว่าค่าเฉลี่ยตัวอย่างจะเท่ากับค่าเฉลี่ยประชากร ซึ่งอาจผิดและผิดเกือบตลอดเวลา ดังนั้นพวกเขาจึงได้แนะนำคำศัพท์เช่นค่า p และช่วงความเชื่อมั่น

ค่า P เป็นวิธีง่ายๆ ในการวัดความน่าจะเป็นของการค้นหาผลลัพธ์ที่สังเกตได้หรือผลลัพธ์สุดขั้วเมื่อสมมติฐานว่างเป็นจริง คุณปฏิเสธสมมติฐานว่างเมื่อค่า p ต่ำกว่าระดับนัยสำคัญที่ 0.05 ตอนนี้ ค่า p และช่วงความเชื่อมั่นมีความสำคัญเพียงพอที่จะระบุบทความแยกต่างหากสำหรับค่าเหล่านี้

ดังนั้น ในขั้นแรก คุณต้องเก็บตัวอย่างจากประชากร คุณทำขั้นตอนซ้ำหลายครั้ง ตอนนี้ ค่าเฉลี่ยที่แท้จริงของคุณควรอยู่ในช่วงความเชื่อมั่นที่คุณเลือก โดยมีความเป็นไปได้ที่แน่นอน นี่คือสิ่งที่คุณต้องทำเพื่อให้ได้ผลลัพธ์สำหรับคำถามการโยนเหรียญของฉัน

คุณอาจกำลังคิดว่า Frequentists นั้นซับซ้อนเกินไป พวกเขาอยู่ในความรู้สึก พวกเขามักจะพบคำตอบสากลที่สมบูรณ์แบบที่ใครๆ ก็ยอมรับได้ แม้จะมีเงื่อนไขต่างกัน และด้วยการทำเช่นนี้ Frequentists เกี่ยวข้องกับการคำนวณและความซับซ้อนที่ร้ายแรง ซึ่งผู้เริ่มต้นอาจไม่เข้าใจ

บทสรุป

Bayesian vs. Frequentist— ทางไหน?

การอภิปรายแบบ Bayesian กับ Frequentist จะดำเนินต่อไป แต่ขึ้นอยู่กับคุณ ตามทรัพยากรที่มีอยู่ ซึ่งแนวทางที่จะใช้ ทั้งสองวิธีมีการใช้งานจำนวนมาก นักคณิตศาสตร์ Laplace ผู้ยิ่งใหญ่ได้คำนวณมวลของดาวเสาร์โดยใช้การอนุมานแบบเบย์ ซึ่งอาจยากกว่ามากเมื่อใช้วิธี Frequentist

ในทางกลับกัน วิธีคิดที่ใช้บ่อยได้ช่วยนักวิจัยล่าสุดในการแก้ปัญหาอย่างมีประสิทธิภาพ โดยเฉพาะอย่างยิ่งในด้านวิทยาศาสตร์การแพทย์ที่ไม่สามารถทำได้ด้วยการอนุมานแบบเบย์

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT- สถานะศิษย์เก่า B, 5+ โครงการหลักที่ใช้งานได้จริง & ความช่วยเหลือด้านงานกับบริษัทชั้นนำ