Байесовцы против частотников: какой из них выбрать для вашей следующей задачи?

Если вы когда-либо занимались статистикой, скорее всего, вы читали о великом споре — байесовцы против частых. Каждый из них представляет собой просто подход к решению статистической задачи, связанной с вероятностями. Теперь байесовские статистики обвиняют в своих методах частых и наоборот. Этим спорам нет конца. Оба имеют свои преимущества и недостатки.

В этой статье мы рассмотрим оба подхода и выясним, какой из них подходит вам для решения вашей следующей статистической задачи.

Байесовцы против частотников — с точки зрения определения вероятности

Определение 1: Вероятность как степень уверенности Фрэнка Рэмси (байесовский подход)

Вероятность события измеряется субъективной степенью уверенности. Его также называют «логической вероятностью». Это означает, что ваше определение вероятности может отличаться от чьего-то другого, если у него или нее больше доказательств, чем у вас. Это совершенно нормально, и другой человек может думать все, что хочет.

Определение 2: Вероятность как долгосрочная частота Рональда Фишера (Подход Frequentists)

Вероятность события равна длительной частоте этого события, когда оно повторяется несколько раз снова и снова. Существует один универсальный ответ, и в отличие от определения 1, мнения о вероятности события не могут различаться от человека к человеку, даже если у них больше/меньше доказательств.

Пример:

Предположим, у меня есть непредвзятая нормальная монета с орлом на одной стороне и решкой на другой. Теперь я бросаю монету. У меня есть результаты. Но вы, как зритель, не знаете, является ли монета орлом или решкой.

Итак, я хочу, чтобы вы ответили: « Какова вероятность того, что монета, которую я подбросил, окажется орлом ?»

Будет два разных вида ответов, основанных на двух разных определениях вероятности .

байесовцы

Байесовцы ответят, что вероятность того, что монета выпадет хедз-ап, составляет 50%. Вы, как байесианец, скажете мне: « Для меня ответ на 50% хедз-ап. Но да, вы знаете результат метания. Итак, у вас есть 100% вероятность того, что монета выпадет либо орлом, либо решкой. Но, знаете что, мне все равно. Потому что, согласно имеющимся у меня ресурсам, ответ для меня составляет 50%. ”

Частые

Часто задаваемые вопросы ответят на вопрос: « Существует либо 100%-ная вероятность, либо 0%-ная вероятность того, что монета выпадет хедз-ап. Поскольку монета приземлилась, нет смысла привязывать вероятность к этому фиксированному и постоянному значению. Результат жеребьевки является окончательным и не подлежит изменению. Ни у кого не будет разночтений в ответе.

Читайте: Типы контролируемого обучения

Байесовцы и частотщики — с точки зрения использования априорных вероятностей

Давайте рассмотрим другой пример.

Мы сделаем приведенный выше пример еще на один шаг. Я буду бросать монету много раз, допустим, 14 раз. Вы записали результаты последних 14 подбрасываний монеты. Теперь в 15-й раз я снова бросаю монету. Теперь вас спрашивают: « Какова вероятность того, что эта подброшенная монета выпадет орлом вверх ».

байесовцы

Если вы байесовец, вы будете использовать термин, известный как априорный . Рассмотрим формулу Байеса для условной вероятности:

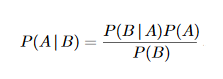
где A и B — некоторые события, а P(A | B) определяется как вероятность события A при условии, что произошло событие B.

Теперь термин P (A) определяется как априорный, который определяется как вероятность того, что событие A истинно до того, как данные будут рассмотрены.

Возвращаясь к примеру, как байесовец, вы будете использовать термин «априорно», т. е. вы примете решение на основе прошлых результатов подбрасывания монеты.

Предположим, что из 14 подбрасываний монеты я попал в хедз-ап 9 раз. Вы можете сказать: «Ну, у меня больше шансов получить голову». Не только вы так говорите, но и ваш расчет подкрепляет ваш аргумент. Таким образом, ваше решение было изменено из-за «предварительных» результатов. Способность человека принимать решения зависит от степени его веры в выбранный априор. Назначение априорных вероятностей было одним из ключевых факторов в результатах Байеса.

Обязательно прочтите: Типы регрессионных моделей в машинном обучении

Частые

Если вы частотист, вы будете полностью не согласны со всем, что говорят байесовцы. Вас не интересует априор, поскольку априор часто представляет собой предполагаемое значение. Скорее ваша идея основана на оценке максимального правдоподобия. Что вы будете делать, так это собирать выборочные данные из населения. Теперь оцените среднее значение, которое в основном совпадает со средним значением данных. Это значение является точкой максимального правдоподобия (оценкой) неопределенного параметра.

Теперь частотщики могут предположить, что среднее значение выборки будет равно среднему значению генеральной совокупности, что может быть неверным и действительно ошибочно в большинстве случаев. Поэтому они ввели такие термины, как p-значения и доверительные интервалы.

P-значение — это простой способ измерить вероятность обнаружения наблюдаемых или экстремальных результатов, когда нулевая гипотеза верна. Вы отклоняете нулевую гипотезу, когда p-значение ниже уровня значимости 0,05. Сейчас значения p и доверительные интервалы настолько важны, что им можно посвятить отдельную статью.

Итак, теперь в качестве первого шага вы собираете выборку из населения. Вы повторяете процедуру большое количество раз. Теперь ваше истинное среднее значение должно находиться в пределах выбранных вами доверительных интервалов с определенной вероятностью. Это то, что вам нужно сделать, чтобы получить ответ на мой вопрос о подбрасывании монеты.

Вы можете подумать, что Frequentists слишком сложны. Ну, они в каком-то смысле. Они склонны находить идеальный универсальный ответ, который может принять каждый, несмотря на различные условия. При этом Frequentists действительно требует серьезных вычислений и сложности, которые новички могут не понять.

Заключение

Байесовский или частотный подход — какой путь?

Дебаты между байесовцами и частотниками будут продолжаться. Но это зависит от вас, исходя из имеющихся ресурсов, какой подход использовать. Оба подхода имеют огромное количество приложений. Великий математик Лаплас рассчитал массу Сатурна с помощью байесовского вывода, который мог бы быть намного сложнее с помощью метода Фреквента.

С другой стороны, фреквентистский образ мышления помог недавним исследователям эффективно решать проблемы, особенно в области медицины, которые нельзя было решить с помощью байесовского вывода.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.