貝葉斯與頻率論者:為您的下一個問題選擇哪一個?
已發表: 2020-12-23如果您曾經研究過統計數據,那麼您很可能已經閱讀過這場偉大的辯論——貝葉斯與頻率論者。 這些中的每一個都只是解決與概率相關的統計問題的一種方法。 現在,貝葉斯統計學家指責頻率論者的方法,反之亦然。 這場辯論沒有盡頭。 兩者都有其優點和缺點。
在本文中,我們將研究這兩種方法,並找出這兩種方法中的哪一種對您的下一個統計問題有好處。
目錄
貝葉斯與頻率論者——在概率定義方面
定義 1:Frank Ramsey 將概率作為信念程度(貝葉斯方法)
事件發生的概率是通過主觀相信程度來衡量的。 它也被稱為“邏輯概率”。 這意味著如果他/她比你有更多的證據,你對概率的定義可能會與其他人不同。 這完全沒問題,其他人可以隨心所欲。
定義 2:作為長期頻率的概率,Ronald Fisher(頻率論者方法)
一個事件的概率等於該事件反復多次重複時的長期頻率。 有一個普遍的答案,與定義 1 不同,對事件概率的看法不會因人而異,即使他們有更多/更少的證據。

例子:
假設我有一個無偏的正常硬幣,一側有正面,另一側有反面。 現在我拋硬幣。 我有結果。 但是,作為旁觀者,您不知道硬幣是正面朝上還是反面朝上。
所以我想讓你回答——“我扔的硬幣是單挑的概率是多少?”
根據概率的兩種不同定義,會有兩種不同的答案。
貝葉斯
貝葉斯主義者會回答說硬幣有 50% 的機會是單挑的。 作為一個貝葉斯主義者,你會對我說:“答案對我來說是 50% 的單挑。 但是,是的,你知道折騰的結果。 所以,你有 100% 的概率硬幣是正面或反面。 但是,你知道嗎,我不在乎。 因為,根據我可用的資源,我的答案是 50%。 ”
常客
常客會回答這個問題“硬幣有 100% 的機會或 0% 的機會是單挑的。 由於硬幣已經落地,因此將概率附加到這個固定不變的值上是沒有用的。 折騰的結果是最終的,沒有任何改變。 任何人的答案都不會有差異。
閱讀:監督學習的類型
貝葉斯與頻率論者——就先驗概率的使用而言
讓我們看另一個例子。

我們將把上面的例子更進一步。 我會擲硬幣很多次,假設是 14 次。 你已經記下了過去 14 次拋硬幣的結果。 現在是第 15 次,我再次拋硬幣。 現在,你被問到,“這枚硬幣正面朝上的概率是多少”。
貝葉斯
如果您是貝葉斯主義者,您將使用的是一個稱為先驗的術語。 讓我們看看條件概率的貝葉斯公式:
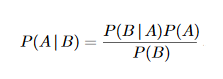
其中 A 和 B 是一些事件,P(A | B) 定義為給定事件 B 發生的事件 A 的概率。
現在,術語 P(A) 被定義為先驗,它被定義為在考慮數據之前事件 A 為真的概率。
回到這個例子,作為貝葉斯人,您將使用先驗一詞,即,您將根據過去拋硬幣的結果做出決定。
假設在 14 次拋硬幣中,我得到了 9 次單挑。 你可能會說“嗯,我有更高的機會得到一個頭”。 不僅你這麼說,而且你的計算也會支持你的論點。 因此,由於“先前”的結果,您的決定已經改變。 一個人的決策能力取決於一個人對所選擇的先驗的信念程度。 分配先驗概率一直是貝葉斯結果的關鍵因素之一。
必讀:機器學習中的回歸模型類型
常客
如果您是頻率論者,您將完全不同意貝葉斯主義者所說的一切。 您對先驗沒有任何興趣,因為先驗通常是一個猜測值。 相反,您的想法是基於最大似然估計。 您將要做的是,您將從人群中收集樣本數據。 現在估計與數據平均值基本一致的平均值。 該值是不確定參數的最大似然點(估計值)。
現在,頻率論者可能會假設樣本均值等於總體均值,這可能是錯誤的,而且在大多數情況下確實是錯誤的。 因此他們引入了諸如 p 值和置信區間之類的術語。
當原假設為真時,P 值是衡量發現觀察到的或極端結果的概率的一種簡單方法。 當 p 值低於顯著性水平 0.05 時,您拒絕原假設。 現在,p 值和置信區間非常重要,足以為它們專門寫一篇文章。
所以現在作為第一步,你從總體中收集樣本。 你重複這個過程很多次。 現在,您的真實均值應該在您選擇的置信區間內,並且具有一定的概率。 這就是你必須做的才能得到我的擲硬幣問題的結果。

你可能認為頻率論太複雜了。 嗯,他們在某種意義上。 他們傾向於找到任何人都可以接受的完美通用答案,儘管有各種條件。 通過這樣做,頻率主義者確實涉及初學者可能無法理解的嚴重計算和復雜性。
結論
貝葉斯 vs. 頻率論——哪一種方式?
貝葉斯與頻率論的辯論將繼續進行。 但是,根據可用的資源,使用哪種方法取決於您。 這兩種方法都有大量的應用。 偉大的數學家拉普拉斯使用貝葉斯推斷來計算土星的質量,而這對於頻率論的方法來說可能會更加困難。
另一方面,頻率論者的思維方式幫助最近的研究人員有效地解決了問題,尤其是在醫學領域,貝葉斯推理無法解決這些問題。
如果您有興趣了解有關機器學習的更多信息,請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑,該文憑專為工作專業人士設計,提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。
