ベイジアン対頻度主義者:次の問題のためにどちらを選択しますか?
公開: 2020-12-23統計に興味を持ったことがある場合は、ベイジアン対頻度主義者という大きな議論について読んだことがあるかもしれません。 これらはそれぞれ、確率に関連する統計的問題を解決するための単なるアプローチです。 現在、ベイジアン統計学者は頻度主義者を彼らの方法で非難し、逆もまた同様です。 この議論に終わりはありません。 どちらにも長所と短所があります。
この記事では、両方のアプローチを調べ、2つのアプローチのうちどちらが次の統計問題に適しているかを調べます。
目次
ベイジアン対頻度主義者—確率の定義の観点から
定義1:フランク・ラムゼイによる信念の程度としての確率(ベイズアプローチ)
イベントの確率は、主観的な信念の程度によって測定されます。 これは「論理確率」とも呼ばれます。 これは、他の人があなたよりも多くの証拠を持っている場合、あなたの確率の定義が他の人の定義と異なる可能性があることを意味します。 これは完全に問題なく、他の人は自分がやりたいことを何でも考えることができます。
定義2:ロナルドフィッシャーによる長期頻度としての確率(頻度主義的アプローチ)
イベントの確率は、イベントが数回繰り返された場合のそのイベントの長期的な頻度に等しくなります。 普遍的な答えが1つあり、定義1とは異なり、イベントの確率に対する意見は、証拠が多かれ少なかれある場合でも、人によって異なることはありません。

例:
片側に頭があり、反対側に尾がある、偏りのない通常のコインがあるとします。 今、私はコインを投げます。 結果があります。 しかし、観客としてのあなたは、コインがヘッズアップかテールアップかを知りません。
だから私はあなたに答えてほしい-「私が投げたコインがヘッズアップである確率はどれくらいですか?」
確率の2つの異なる定義に基づいて、2つの異なる種類の回答があります。
ベイジアン
ベイジアンは、コインがヘッズアップである可能性が50%あると答えます。 ベイジアンとしてのあなたは私にこう言います。「答えは私にとって50%のヘッズアップです。 しかし、ええ、あなたは投げの結果を知っています。 したがって、コインが表または裏のいずれかである確率は100%です。 しかし、あなたは何を知っていますか、私は気にしません。 なぜなら、私が利用できるリソースによると、答えは私にとって50%です。 」
頻度主義者
頻度主義者は、「コインがヘッズアップである可能性は100%または0%のいずれかです。 コインが着地したので、この固定された一定の値に確率を付けることには意味がありません。 トスの結果は最終的なものであり、変更はありません。 誰もが答えにばらつきはありません。
読む:教師あり学習の種類
ベイジアン対頻度主義者—事前確率の使用に関して
別の例を見てみましょう。
上記の例をさらに一歩進めます。 コインを何度も投げます。14回としましょう。 あなたは過去14回のコイン投げの結果を書き留めました。 今度は15回目ですが、またコインを投げます。 さて、あなたは「この投げられたコインがヘッズアップである確率はどれくらいですか」と尋ねられます。

ベイジアン
あなたがベイジアンである場合、あなたが使用するものは、 priorとして知られている用語です。 条件付き確率のベイズの公式を調べてみましょう。
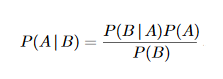
ここで、AとBはいくつかのイベントであり、P(A | B)はイベントAの確率として定義されます。特定のイベントBが発生しました。
ここで、用語P(A)は事前定義として定義されます。これは、データが考慮される前にイベントAが真である確率として定義されます。
例に戻ると、ベイジアンとして、以前の用語を使用します。つまり、過去のコイン投げの結果に基づいて決定を下します。
14回のコイン投げのうち、9回ヘッズアップしたとします。 「まあ、頭が出る可能性が高い」と言うかもしれません。 あなたがそれを言うだけでなく、あなたの計算もあなたの議論をサポートするでしょう。 したがって、「以前の」結果のためにあなたの決定は変更されました。 決定を下す能力は、選択した事前の信念の程度に依存します。 事前確率の割り当ては、ベイジアンの結果の重要な要素の1つです。
必読:機械学習における回帰モデルの種類
頻度主義者
あなたが頻度主義者であるならば、あなたはベイジアンが言うことには完全に反対するでしょう。 事前情報は推測値であることが多いため、事前情報には関心がありません。 むしろ、あなたのアイデアは最尤推定に基づいています。 あなたがすることは、母集団からサンプルデータを収集することです。 ここで、データの平均とほぼ均一な平均値を推定します。 この値は、不確実なパラメーターの最尤点(推定)です。
さて、頻度主義者は、サンプルの平均が母集団の平均に等しいと想定するかもしれません。これは間違っている可能性があり、ほとんどの場合実際に間違っています。 そのため、p値や信頼区間などの用語が導入されました。
P値は、帰無仮説が真である場合に観測された結果または極端な結果を見つける確率を測定する簡単な方法です。 p値が有意水準0.05を下回る場合、帰無仮説を棄却します。 現在、p値と信頼区間は、それらに別の記事を捧げるのに十分重要です。
したがって、最初のステップとして、母集団からサンプルを収集します。 手順を何度も繰り返します。 これで、真の平均は選択した信頼区間内にあり、一定の確率があります。 これは、私のコイントスの質問の結果を得るためにあなたがしなければならないことです。

あなたは頻度主義者があまりにも複雑だと思っているかもしれません。 そうですね、ある意味でそうです。 彼らは、さまざまな条件にもかかわらず、誰でも受け入れることができる完璧な普遍的な答えを見つける傾向があります。 そしてそうすることによって、頻度主義者は初心者が理解できないかもしれない深刻な計算と複雑さを伴います。
結論
ベイジアン対頻度主義—どちらが方法ですか?
ベイジアン対頻度主義の議論は続くでしょう。 しかし、利用可能なリソースに基づいて、どのアプローチを使用するかはあなた次第です。 どちらのアプローチにも、膨大な数のアプリケーションがあります。 偉大な数学者ラプラスは、ベイズ推定を使用して土星の質量を計算しました。これは、頻度主義的方法では非常に困難であった可能性があります。
一方、頻度主義的考え方は、最近の研究者が、特にベイズ推定では不可能だった医学の分野で問題を効率的に解決するのに役立ちました。
機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。
