Bayesian kontra Frequentists: który wybrać dla następnego problemu?

Jeśli kiedykolwiek interesowałeś się statystykami, prawdopodobnie czytałeś o wielkiej debacie — Bayesian vs. Frequentists. Każdy z nich jest jedynie podejściem do rozwiązania problemu statystycznego związanego z prawdopodobieństwem. Teraz statystycy bayesowscy obwiniają Frequentystów za ich metody i vice versa. Ta debata nie ma końca. Oba mają swoje wady i zalety.

W tym artykule przyjrzymy się obu podejściom i dowiemy się, które z nich jest dla Ciebie dobre w przypadku następnego problemu statystycznego.

Bayesowie kontra Frequentyści — w kategoriach definicji prawdopodobieństwa

Definicja 1: Prawdopodobieństwo jako stopień wiary według Franka Ramseya (podejście bayesowskie)

Prawdopodobieństwo zdarzenia mierzy się subiektywnym stopniem wiary. Nazywa się to również „prawdopodobieństwem logicznym”. Oznacza to, że twoja definicja prawdopodobieństwa może różnić się od definicji innej osoby, jeśli ta osoba ma więcej dowodów niż ty. To jest całkowicie w porządku, a druga osoba może myśleć, co chce.

Definicja 2: Prawdopodobieństwo jako częstotliwość długoterminowa według Ronalda Fishera (podejście częstych)

Prawdopodobieństwo zdarzenia jest równe długookresowej częstotliwości tego zdarzenia, gdy powtarza się kilka razy w kółko. Jest jedna uniwersalna odpowiedź i w przeciwieństwie do definicji 1, opinie na temat prawdopodobieństwa zdarzenia nie mogą się różnić w zależności od osoby, nawet jeśli mają więcej/mniej dowodów.

Przykład:

Załóżmy, że mam bezstronną normalną monetę z orzełkami po jednej stronie i remkami po drugiej. Teraz rzucam monetą. Mam wyniki. Ale ty jako widz nie wiesz, czy moneta jest heads-up, czy tails-up.

Więc chcę, żebyś odpowiedział – „ Jakie jest prawdopodobieństwo, że moneta, którą rzuciłem, jest heads-up ?”

Będą dwa różne rodzaje odpowiedzi w oparciu o dwie różne definicje prawdopodobieństwa .

Bayesowie

Bayesowie odpowiedzą, że istnieje 50% szans na to, że moneta wypadnie heads-up. Ty, jako Bayesian, powiesz mi: „ Odpowiedź brzmi dla mnie w 50% heads-up. Ale tak, znasz wynik rzucania. Masz więc 100% prawdopodobieństwa, że ​​moneta jest orłem lub reszekem. Ale wiesz co, nie obchodzi mnie to. Ponieważ zgodnie z dostępnymi mi zasobami odpowiedź to dla mnie 50%. ”

Frekwentyści

Frequentyści odpowiedzą na pytanie „ Istnieje albo 100%, albo 0% szans, że moneta wypadnie jeden na jednego. Ponieważ moneta została wyładowana, nie ma sensu przypisywać prawdopodobieństwa do tej stałej i stałej wartości. Wynik rzutu jest ostateczny i nie ma w nim żadnych zmian. Nie będzie żadnej odmiany odpowiedzi wśród nikogo.

Przeczytaj: Rodzaje nadzorowanego uczenia się

Bayesowie kontra częstyści — w kategoriach wykorzystania wcześniejszych prawdopodobieństw

Spójrzmy na inny przykład.

Powyższy przykład pójdziemy o krok dalej. Będę rzucał monetą wiele razy, przypuśćmy, że 14 razy. Zanotowałeś wyniki ostatnich 14 rzutów monetą. Teraz po raz piętnasty ponownie rzucam monetą. Teraz zostaniesz zapytany: „ Jakie jest prawdopodobieństwo, że ta rzucona moneta wypadnie heads-up ”.

Bayesowie

Jeśli jesteś bayesowcem, użyjesz terminu znanego jako prior . Przyjrzyjmy się wzorowi Bayesa na prawdopodobieństwo warunkowe:

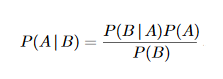
gdzie A i B są pewnymi zdarzeniami, a P(A | B) jest zdefiniowane jako prawdopodobieństwo zdarzenia A dane zdarzenie B miało miejsce.

Teraz termin P(A) jest zdefiniowany jako wcześniejszy, co jest definiowane jako prawdopodobieństwo, że zdarzenie A jest prawdziwe, zanim dane zostaną wzięte pod uwagę.

Wracając do przykładu, jako Bayesa użyjesz terminu „przed”, tj. podejmiesz decyzję na podstawie wcześniejszych wyników rzucania monetą.

Załóżmy, że na 14 rzutów monetą trafiłem heads-up 9 razy. Można powiedzieć, że „Cóż, mam większe szanse na zdobycie głowy”. Nie tylko ty to mówisz, ale twoje obliczenia będą również wspierać twoją argumentację. Więc twoja decyzja została zmieniona z powodu „wcześniejszych” wyników. Zdolność do podejmowania decyzji zależy od stopnia wiary w wybranego przełożonego. Przypisywanie wcześniejszych prawdopodobieństw było jednym z kluczowych czynników wpływających na wyniki Bayesiana.

Musisz przeczytać: rodzaje modeli regresji w uczeniu maszynowym

Frekwentyści

Jeśli jesteś Frequentystą, całkowicie nie zgodzisz się z tym, co mówią Bayesowie. Nie interesujesz się przeorem, ponieważ przeor jest często zgadywaną wartością. Twój pomysł opiera się raczej na oszacowaniu maksymalnego prawdopodobieństwa. Co zrobisz, to zbierzesz przykładowe dane z populacji. Teraz oszacuj wartość średnią, która jest w większości jednolita ze średnią danych. Ta wartość jest punktem największego prawdopodobieństwa (oszacowaniem) niepewnego parametru.

Frequentyści mogą teraz założyć, że średnia z próby byłaby równa średniej populacji, co może być błędne i rzeczywiście jest błędne przez większość czasu. Wprowadzili więc takie terminy, jak wartości p i przedziały ufności.

Wartość P to prosty sposób pomiaru prawdopodobieństwa znalezienia zaobserwowanych lub skrajnych wyników, gdy hipoteza zerowa jest prawdziwa. Hipotezę zerową odrzucasz, gdy wartość p jest poniżej poziomu istotności 0,05. Teraz wartości p i przedziały ufności są wystarczająco ważne, aby poświęcić im osobny artykuł.

Więc teraz, jako pierwszy krok, pobierz próbkę z populacji. Powtarzasz tę procedurę wiele razy. Twoja prawdziwa średnia powinna mieścić się w wybranych przedziałach ufności, z pewnym prawdopodobieństwem. Oto, co musisz zrobić, aby uzyskać wynik mojego pytania o rzucanie monetą.

Być może myślisz, że częstowcy są zbyt skomplikowani. Cóż, w pewnym sensie są. Mają tendencję do znajdowania idealnej uniwersalnej odpowiedzi, która może być zaakceptowana przez każdego, niezależnie od różnych warunków. W ten sposób Frequentyści wiążą się z poważnymi obliczeniami i złożonością, których początkujący mogą nie zrozumieć.

Wniosek

Bayesowski vs. Frequentysta — jaka jest droga?

Debata bayesowska i częsta będzie się toczyć. Ale to zależy od ciebie, w oparciu o dostępne zasoby, z którego podejścia skorzystać. Oba podejścia mają ogromną liczbę zastosowań. Wielki matematyk Laplace obliczył masę Saturna za pomocą wnioskowania bayesowskiego, co mogło być o wiele trudniejsze w przypadku metody Frequentisa.

Z drugiej strony, częsty sposób myślenia pomógł niedawnym badaczom w skutecznym rozwiązywaniu problemów, zwłaszcza w dziedzinie nauk medycznych, których nie można było osiągnąć za pomocą wnioskowania bayesowskiego.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.