Bayésiens contre fréquentistes : lequel choisir pour votre prochain problème ?

Si vous avez déjà été dans les statistiques, il y a de fortes chances que vous ayez lu le grand débat Bayesian vs Frequentists. Chacun d'entre eux n'est qu'une approche pour résoudre un problème statistique lié aux probabilités. Maintenant, les statisticiens bayésiens blâment les fréquentistes pour leurs méthodes et vice-versa. Il n'y a pas de fin à ce débat. Les deux ont leurs avantages et leurs inconvénients.

Dans cet article, nous examinerons les deux approches et découvrirons laquelle des deux vous convient le mieux pour votre prochain problème statistique.

Bayésiens contre fréquentistes - En termes de définition de probabilité

Définition 1 : La probabilité comme degré de croyance par Frank Ramsey (approche bayésienne)

La probabilité d'un événement est mesurée par le degré subjectif de croyance. On l'appelle aussi la « probabilité logique ». Cela signifie que votre définition de la probabilité peut différer de celle de quelqu'un d'autre, s'il a plus de preuves que vous. C'est très bien et l'autre personne peut penser ce qu'elle veut.

Définition 2 : probabilité comme fréquence à long terme par Ronald Fisher (approche fréquentiste)

La probabilité d'un événement est égale à la fréquence à long terme de cet événement lorsqu'il se répète plusieurs fois. Il existe une réponse universelle et contrairement à la définition 1, les opinions sur la probabilité d'un événement ne peuvent pas varier d'une personne à l'autre même si elles ont plus ou moins de preuves.

Exemple:

Supposons que j'ai une pièce de monnaie normale non biaisée ayant des têtes d'un côté et des queues de l'autre. Maintenant, je lance la pièce. J'ai les résultats. Mais, en tant que spectateur, vous ne savez pas si la pièce est pile ou face.

Donc, je veux que vous répondiez - " Quelle est la probabilité que la pièce que j'ai lancée soit en tête-à-tête ?"

Il y aura deux types de réponses différents basés sur les deux définitions différentes de la probabilité .

Bayésiens

Les bayésiens répondront qu'il y a 50% de chances que la pièce soit en tête-à-tête. En tant que bayésien, vous me direz : « La réponse est 50 % heads-up pour moi. Mais oui, vous connaissez le résultat du lancer. Ainsi, vous avez une probabilité de 100 % que la pièce soit pile ou face. Mais, vous savez quoi, je m'en fous. Car, selon les ressources dont je dispose, la réponse est 50% pour moi. ”

Fréquentistes

Les fréquentistes répondront à la question « Il y a soit 100 % de chances, soit 0 % de chances que la pièce soit en tête-à-tête. Puisque la pièce a été débarquée, il est inutile d'attacher une probabilité à cette valeur fixe et constante. Le résultat du lancer est définitif et ne subit aucune modification. Il n'y aura aucune variation de réponse parmi quiconque.

Lire : Types d'apprentissage supervisé

Bayésiens contre fréquentistes - en termes d'utilisation des probabilités a priori

Examinons un autre exemple.

Nous allons pousser l'exemple ci-dessus un peu plus loin. Je lancerai la pièce plusieurs fois, supposons 14 fois. Vous avez noté les résultats des 14 derniers lancers de pièces. Maintenant, pour la 15e fois, je lance à nouveau la pièce. Maintenant, on vous demande, " Quelle est la probabilité que cette pièce lancée soit tête haute ".

Bayésiens

Si vous êtes bayésien, ce que vous utiliserez, c'est un terme connu sous le nom de prior . Examinons la formule de Bayes pour la probabilité conditionnelle :

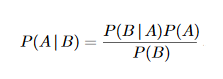
où A et B sont des événements et P(A | B) est défini comme la probabilité que l'événement A donné l'événement B se soit produit.

Maintenant, le terme P(A) est défini comme a priori qui est défini comme la probabilité que l'événement A soit vrai avant que les données ne soient prises en compte.

Pour en revenir à l'exemple, en tant que bayésien, vous utiliserez le terme prior, c'est-à-dire que vous prendrez une décision basée sur les résultats passés des lancers de pièces.

Supposons que sur 14 tirages au sort, j'ai eu 9 fois le tête-à-tête. Vous pourriez dire que "Eh bien, j'ai plus de chances d'avoir une tête". Non seulement vous dites cela, mais votre calcul va également étayer votre argumentation. Votre décision a donc été modifiée en raison des résultats « antérieurs ». La capacité d'une personne à prendre des décisions dépend de son degré de croyance dans le prior choisi. L'attribution de probabilités a priori a été l'un des facteurs clés des résultats de Bayesian.

Doit lire : Types de modèles de régression dans l'apprentissage automatique

Fréquentistes

Si vous êtes un fréquentiste, vous serez complètement en désaccord avec tout ce que disent les bayésiens. Vous n'avez aucun intérêt dans le prior car le prior est souvent une valeur devinée. Votre idée est plutôt basée sur l'estimation du maximum de vraisemblance. Ce que vous allez faire, c'est collecter des données d'échantillon auprès d'une population. Estimez maintenant la valeur moyenne qui est la plupart du temps uniforme avec la moyenne des données. Cette valeur est le point de vraisemblance maximum (estimation) du paramètre incertain.

Maintenant, les fréquentistes pourraient supposer que la moyenne de l'échantillon serait égale à la moyenne de la population, ce qui pourrait être faux et est en effet faux la plupart du temps. Ils ont donc introduit des termes tels que p-values ​​et intervalles de confiance.

La valeur P est un moyen simple de mesurer la probabilité de trouver des résultats observés ou extrêmes lorsque l'hypothèse nulle est vraie. Vous rejetez l'hypothèse nulle lorsque la valeur de p est inférieure au seuil de signification de 0,05. Désormais, les valeurs de p et les intervalles de confiance sont suffisamment importants pour leur consacrer un article distinct.

Alors maintenant, dans un premier temps, vous collectez l'échantillon de la population. Vous répétez la procédure un grand nombre de fois. Maintenant, votre véritable moyenne doit se situer dans les intervalles de confiance que vous choisissez, avec une certaine probabilité. C'est ce que vous devez faire pour obtenir le résultat de ma question à pile ou face.

Vous pensez peut-être que les fréquentistes sont beaucoup trop complexes. Eh bien, ils le sont en un sens. Ils ont tendance à trouver la réponse universelle parfaite qui peut être acceptée par n'importe qui, malgré diverses conditions. Et ce faisant, les fréquentistes impliquent des calculs sérieux et une complexité que les débutants pourraient ne pas comprendre.

Conclusion

Bayésien contre fréquentiste - quelle est la voie ?

Le débat bayésien contre fréquentiste se poursuivra. Mais c'est à vous, en fonction des ressources disponibles, quelle approche utiliser. Les deux approches ont leur grand nombre d'applications. Le grand mathématicien Laplace a calculé la masse de Saturne en utilisant l'inférence bayésienne qui aurait pu être beaucoup plus difficile avec la méthode fréquentiste.

D'autre part, la façon de penser fréquentiste a aidé les chercheurs récents à résoudre efficacement des problèmes, en particulier dans le domaine de la science médicale, ce qui n'aurait pas pu être fait avec l'inférence bayésienne.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.