بايزي مقابل المتكرر: أيهما تختار لمشكلتك التالية؟

إذا سبق لك أن دخلت في الإحصائيات ، فمن المحتمل أنك قرأت عن الجدل الكبير - بايزي مقابل المتكرر. كل من هذه هي مجرد نهج لحل مشكلة إحصائية تتعلق بالاحتمالات. الآن ، يلقي الإحصائيون في نظرية بايز باللوم على المترددين على أساليبهم والعكس صحيح. لا يوجد حد لهذا النقاش. كلاهما لديهم فوائد ومساويء.

في هذه المقالة ، سننظر في كلا النهجين ونكتشف أيهما مناسب لك لمشكلتك الإحصائية التالية.

Bayesians مقابل المتكررة - من حيث تعريف الاحتمالية

التعريف 1: الاحتمالية كدرجة من الاعتقاد بقلم فرانك رامزي (نهج بايزي)

يتم قياس احتمالية حدوث حدث من خلال درجة الاعتقاد الذاتية. ويسمى أيضًا "الاحتمال المنطقي". هذا يعني أن تعريفك للاحتمال قد يختلف عن تعريف شخص آخر ، إذا كان لديه / لديها دليل أكثر منك. هذا جيد تمامًا ويمكن للشخص الآخر أن يفكر في ما يريد.

التعريف 2: الاحتمالية كتكرار طويل المدى بواسطة رونالد فيشر (النهج المتكرر)

احتمالية حدوث حدث تساوي التكرار طويل المدى لذلك الحدث عندما يتكرر عدة مرات مرارًا وتكرارًا. هناك إجابة عالمية واحدة ، وعلى عكس التعريف 1 ، لا يمكن أن تختلف الآراء حول احتمالية وقوع حدث من شخص لآخر حتى لو كانت لديها أدلة أكثر / أقل.

مثال:

لنفترض أن لدي عملة عادية غير متحيزة برأس من جهة وذيول من جهة أخرى. الآن أرمي العملة. لدي النتائج. لكنك كمتفرج لا تعرف ما إذا كانت العملة وجهًا لوجه أم لا.

لذا أريدك أن تجيب - " ما هو احتمال أن تكون العملة التي رميتها هي رأسًا على عقب ؟"

سيكون هناك نوعان مختلفان من الإجابات بناءً على التعريفين المختلفين للاحتمال .

بايزي

سوف يجيب Bayesians بأن هناك احتمال بنسبة 50٪ أن تكون العملة المعدنية رأسًا على عقب. ستقول لي باعتبارك بايزي ، " الإجابة هي 50٪ تنبيه. لكن نعم ، أنت تعرف نتيجة القذف. لذلك ، لديك احتمال بنسبة 100٪ أن تكون العملة إما رأسية أو ذيلًا. لكن ، أنت تعرف ماذا ، أنا لا أهتم. لأنه ، حسب الموارد المتاحة لي ، الإجابة هي 50٪ بالنسبة لي. "

كثرة

سيجيب المتكررون على السؤال " هناك احتمال بنسبة 100٪ أو احتمال بنسبة 0٪ أن تكون العملة وجهًا لوجه. منذ أن تم إنزال العملة المعدنية ، فلا فائدة من إرفاق احتمالية بهذه القيمة الثابتة والثابتة. نتيجة القذف نهائية ولا تغيير فيها. لن يكون هناك اختلاف في الإجابة بين أي شخص.

اقرأ: أنواع التعلم الخاضع للإشراف

بايزي مقابل المتكرر - من حيث استخدام الاحتمالات السابقة

دعونا ننظر في مثال آخر.

سوف نأخذ المثال أعلاه خطوة إلى الأمام. سوف أرمي العملة عدة مرات ، لنفترض 14 مرة. لقد قمت بتدوين نتائج آخر 14 عملية رمى للعملة. الآن للمرة الخامسة عشرة ، أرمي العملة مرة أخرى. الآن ، يُطلب منك ، " ما هو احتمال أن تكون هذه العملة المقذوفة رأسًا على عقب ".

بايزي

إذا كنت بايزي ، فإن ما ستستخدمه ، هو مصطلح يُعرف باسم سابق . دعونا نلقي نظرة على صيغة بايز للاحتمال الشرطي:

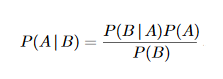
حيث A و B عبارة عن بعض الأحداث ويتم تعريف P (A | B) على أنه احتمال وقوع حدث A معين حدث B.

الآن ، يتم تعريف المصطلح P (A) على أنه سابق والذي يتم تعريفه على أنه احتمال أن يكون الحدث A صحيحًا قبل النظر في البيانات.

بالعودة إلى المثال ، باعتبارك بايزي ، سوف تستخدم المصطلح السابق ، أي أنك ستتخذ قرارًا بناءً على النتائج السابقة لقذف العملات المعدنية.

لنفترض أنه من بين 14 رمية للعملة ، تلقيت تنبيهًا 9 مرات. قد تقول "حسنًا ، لدي فرص أكبر في الحصول على رأس". أنت لا تقول ذلك فحسب ، بل إن حساباتك ستدعم أيضًا حجتك. لذلك تم تغيير قرارك بسبب النتائج "السابقة". تعتمد قدرة المرء على اتخاذ القرارات على درجة إيمانه بما تم اختياره مسبقًا. كان تعيين الاحتمالات السابقة أحد العوامل الرئيسية في نتائج Bayesian.

يجب أن تقرأ: أنواع نماذج الانحدار في التعلم الآلي

كثرة

إذا كنت متكررًا ، فستختلف تمامًا مع ما يقوله Bayesians. ليس لديك أي اهتمام بالسابق حيث أن القيمة السابقة غالبًا ما تكون قيمة تخمينية. بالأحرى تعتمد فكرتك على تقدير الاحتمال الأقصى. ما ستفعله هو جمع بيانات عينة من السكان. الآن قم بتقدير القيمة المتوسطة التي تكون في الغالب موحدة مع متوسط ​​البيانات. هذه القيمة هي أقصى نقطة احتمال (تقدير) للمعلمة غير المؤكدة.

الآن ، قد يفترض المتكررون أن متوسط ​​العينة سيكون مساويًا لمتوسط ​​السكان ، والذي قد يكون خاطئًا وهو خاطئ بالفعل في معظم الأوقات. لذا فقد أدخلوا مصطلحات مثل قيم p وفواصل الثقة.

P-value طريقة بسيطة لقياس احتمالية إيجاد نتائج ملحوظة أو متطرفة عندما تكون الفرضية الصفرية صحيحة. ترفض الفرضية الصفرية عندما تكون القيمة الاحتمالية أقل من مستوى الأهمية 0.05. الآن ، تعتبر قيم p وفواصل الثقة مهمة بما يكفي لتخصيص مقال منفصل لهم.

والآن كخطوة أولى ، تقوم بجمع العينة من السكان. تكرر الإجراء عدة مرات. الآن ، يجب أن يكون الوسط الحقيقي الخاص بك ضمن فترات الثقة التي تختارها ، مع وجود احتمال معين. هذا ما عليك فعله للحصول على نتيجة سؤالي الخاص بإلقاء العملة.

قد تعتقد أن المتكررون هم طريقة معقدة للغاية. حسنًا ، هم بمعنى ما. إنهم يميلون إلى العثور على إجابة عالمية مثالية يمكن لأي شخص قبولها ، على الرغم من الظروف المختلفة. ومن خلال القيام بذلك ، ينطوي المتكررون على حسابات جادة وتعقيدات قد لا يفهمها المبتدئون.

خاتمة

بايزي مقابل المتردد - ما هو الطريق؟

سيستمر النقاش بايزي مقابل الجدل المتكرر. ولكن عليك ، بناءً على الموارد المتاحة ، طريقة الاستخدام. كلا النهجين لهما عدد كبير من التطبيقات. قام عالم الرياضيات العظيم لابلاس بحساب كتلة زحل باستخدام الاستدلال البايزي الذي كان من الممكن أن يكون أكثر صرامة مع الطريقة المتكررة.

من ناحية أخرى ، ساعدت طريقة التفكير المتكرر الباحثين الجدد في حل المشكلات بكفاءة خاصة في مجال العلوم الطبية التي لم يكن من الممكن إجراؤها باستخدام الاستدلال البايزي.

إذا كنت مهتمًا بمعرفة المزيد حول التعلم الآلي ، فراجع دبلوم PG في IIIT-B & upGrad في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، IIIT- حالة الخريجين B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع أفضل الشركات.