Bayesian Networks: บทนำ ตัวอย่าง และการใช้งานจริง
เผยแพร่แล้ว: 2020-02-23ผู้ที่เคยทำงานกับข้อมูลหรือสถิติล้วนทราบสิ่งหนึ่งอย่างแน่นอน: ความสัมพันธ์ไม่จำเป็นต้องหมายถึงหรือบอกเป็นนัยถึงสาเหตุ แม้ว่าสิ่งนี้อาจฟังดูชัดเจน แต่อาจทำให้คุณตกใจเมื่อรู้ว่าข้อผิดพลาดส่วนใหญ่ในข้อมูลเกิดขึ้นเนื่องจากความสับสนระหว่างคำสองคำ โดยหลักแล้วเนื่องจากสะดวกที่จะกำหนดความสัมพันธ์ แต่ก็แทบจะเป็นไปไม่ได้เลยที่จะกำหนดหรือหาปริมาณของสาเหตุ
อันที่จริง Judea Pearl ผู้เขียน Causality: Models, Reasoning และ Inference กล่าวไว้ในหนังสือว่ามนุษย์มุ่งเน้นความพยายามทางคณิตศาสตร์ของพวกเขาในการอนุมานความน่าจะเป็นและทางสถิติ โดยปล่อยให้การพิจารณาเชิงสาเหตุ “อยู่ในความเมตตาของสัญชาตญาณและการตัดสินที่ดี” เขาบอกว่านี่เป็นปัจจัยสำคัญที่เรายังล้าหลังอย่างมากในแง่ของความก้าวหน้าทางวิทยาศาสตร์
นี่คือช่วงเวลาที่ Bayesian Networks ทำให้มันง่ายสำหรับเรา สิ่งเหล่านี้ช่วยให้เราแยกแยะความสัมพันธ์จากสาเหตุโดยทำให้เรามองเห็นสาเหตุอิสระต่างๆ ได้ในคราวเดียว ทั้งหมดนี้ทำได้อย่างแม่นยำเนื่องจากอัลกอริธึมการเรียนรู้ของเครื่องไม่ทำงานบนอัตวิสัยหรือสัญชาตญาณ พวกเขาทำงานกับข้อมูล
มาดูตัวอย่างเพื่อทำความเข้าใจว่า Bayesian Networks ทำงานอย่างไร
สารบัญ
ตัวอย่าง Bayesian Networks
เพื่อประโยชน์ของตัวอย่างนี้ ให้เราสมมติว่าโลกนี้เป็นโรคที่หายากมากแต่ถึงขั้นเสียชีวิต บอกว่ามีโอกาส 1 ใน 1000 ที่คุณจะติดโรคนี้
ทีนี้ เพื่อหาว่ามีใครบางคนกำลังเป็นโรคนี้อยู่หรือไม่ แพทย์จึงทำการทดสอบ สิ่งที่จับได้คือความแม่นยำเพียง 99% เท่านั้น

คุณจะรู้ได้อย่างไรว่าคุณมีโรคหรือไม่? การทดสอบอื่นจะส่งผลต่อผลลัพธ์หรือไม่?
มาดูกันว่าจะเกิดอะไรขึ้นเมื่อคุณทำ...
ทดสอบ 1
เนื่องจากโรคนี้ส่งผลกระทบเพียง 1 ใน 1,000 ความน่าจะเป็นที่คุณจะติดเชื้อคือ:
| ติดเชื้อแล้ว | 0.001 |
| ฟรี | 0.999 |
โรค CPT (ตารางความน่าจะเป็นแบบมีเงื่อนไข)
เห็นได้ชัดว่า 1 ใน 1,000 มีโอกาสเป็นโรคนี้ 999 ใน 1,000 ก็ปลอดจากโรคเช่นกัน
ในทำนองเดียวกัน เราจะสร้างตารางเพื่อคำนวณความน่าจะเป็นของการทดสอบ อย่างที่บอกไปก่อนหน้านี้ว่าหากทดสอบในความแม่นยำเพียง 99% นั่นหมายความว่ามีโอกาสเพียง 99% ที่ผลลัพธ์จะเป็นจริง กรณีที่คล้ายกันกับผลลัพธ์เชิงลบ
| การปรากฏตัวของไวรัส | ติดเชื้อแล้ว | ฟรี |
| ทดสอบ 1 (บวก) | 0.99 | 0.01 |
| ทดสอบ 1 (เชิงลบ) | 0.01 | 0.99 |
Test1 CPT (ตารางความน่าจะเป็นแบบมีเงื่อนไข)
ตอนนี้ เรามาพลอตกราฟเพื่อดูว่าการมีอยู่ของโรคได้รับผลกระทบจากผลการทดสอบอย่างไร
การเติมเซลล์เหล่านี้ด้วยผลการทดสอบจะให้ผลลัพธ์ต่อไปนี้แก่ฉัน

ที่มาของภาพ
อย่างที่คุณเห็น หากผลการทดสอบออกมาเป็นบวก มีโอกาสเพียง 9% ที่คุณจะเป็นโรคนี้
แล้วเราได้เบอร์นี้มาได้ยังไง?
ทฤษฎีบทเบย์!
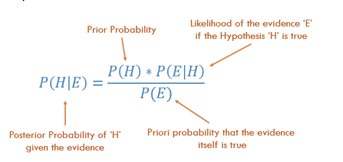
ที่มาของภาพ
ในตัวอย่างของเรา
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0.99 x 0.001) / (0.001 x 0.99 + 0.999 x 0.01) = 0.9 = 9%
สิ่งนี้บอกอะไรเรา?
แม้ว่าการทดสอบจะเป็นบวก เนื่องจากโรคหายาก จึงมีโอกาสเกิดโรคเพียง 9%
ดังนั้น จะเกิดอะไรขึ้นเมื่อคุณทำการทดสอบอีกครั้งเพื่อให้แน่ใจ และผลก็ออกมาในเชิงบวกเช่นกัน
อ่าน: แนวคิดโครงการแมชชีนเลิร์นนิงสำหรับผู้เริ่มต้น
ทดสอบ2
อีกครั้ง การทดสอบครั้งที่สองจะมีความแม่นยำเพียง 99% เช่นกัน
| การปรากฏตัวของไวรัส | ติดเชื้อแล้ว | ฟรี |
| ทดสอบ 2 (บวก) | 0.99 | 0.01 |
| การทดสอบ 2 (เชิงลบ) | 0.01 | 0.99 |
เครือข่ายเบย์เซียนในตอนนี้จะเป็น:
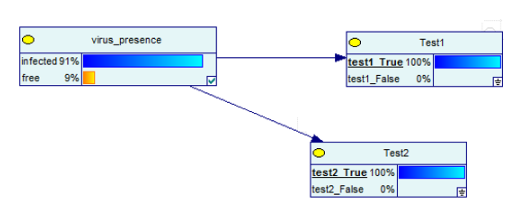
ที่มาของภาพ
ผลลัพธ์กลับกลายเป็น!
ซึ่งหมายความว่าหากคุณได้รับผลบวกสองครั้งจากการทดสอบสองครั้ง โอกาสในการติดไวรัสจะเพิ่มขึ้นจาก 9% เป็น 91% แต่ย้ำว่าไม่ 100%!
ทีนี้จะเกิดอะไรขึ้นถ้าคุณได้รับผลบวกหนึ่งผลและผลลบหนึ่งรายการจากการทดสอบ
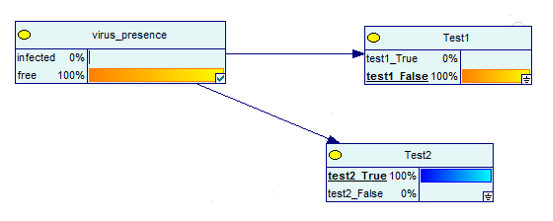
ที่มาของภาพ
อย่างที่คุณเห็น มีโอกาส 100% ที่คุณจะไม่มีโรคนี้ ในกรณีที่การทดสอบหนึ่งในสองรายการเป็นลบ

ทดสอบ 3
มันจะดียิ่งขึ้นไปอีกเมื่อคุณทำการทดสอบสามครั้งและการทดสอบทั้งหมดนั้นเป็นจริง
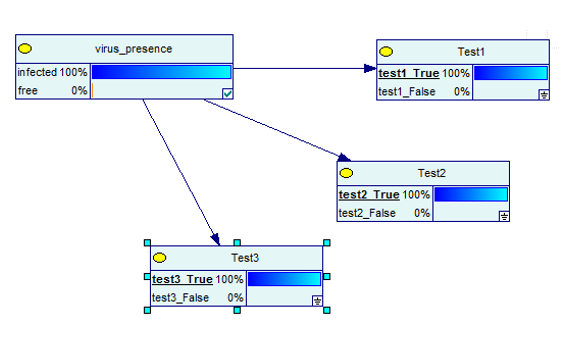
ที่มาของภาพ
เห็นได้ชัดว่าตอนนี้มีโอกาส 100% ที่คุณจะติดเชื้อ
ทีนี้มาดูกันว่าจะเกิดอะไรขึ้นเมื่อการทดสอบอันใดอันหนึ่งเป็นลบ แต่อีกสองอันเป็นบวก
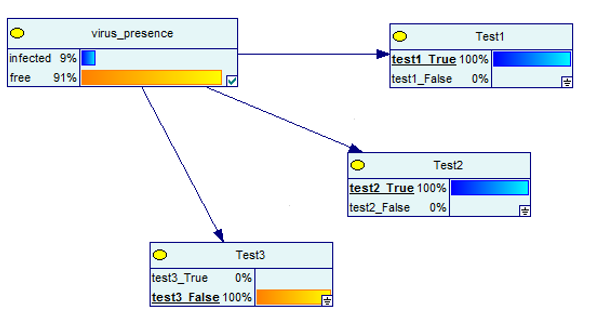
ที่มาของภาพ
อีกครั้ง ผลลัพธ์เป็นบวก 91% สำหรับการมีอยู่ของไวรัส
เครือข่ายเบย์เซียนและการสร้างแบบจำลองข้อมูล
ในตัวอย่างข้างต้น จะเห็นได้ว่า Bayesian Networks มีบทบาทสำคัญในการสร้างแบบจำลองข้อมูลเพื่อให้ได้ผลลัพธ์ที่แม่นยำ
ที่จริงแล้ว การปรับแต่งเครือข่ายโดยรวมปัจจัยอื่นๆ ที่อาจส่งผลต่อผลลัพธ์ยังช่วยให้เราเห็นภาพและจำลองสถานการณ์ต่างๆ โดยใช้ Bayesian Networks
Bayesian Networks เป็นเครื่องมือที่ยอดเยี่ยมในการวัดค่าความไม่เป็นธรรมในข้อมูลและเทคนิคการดูแลจัดการเพื่อลดความไม่เป็นธรรมนี้
ในกรณีเช่นนี้ เป็นการดีที่สุดที่จะใช้เทคนิคเฉพาะเส้นทางเพื่อระบุปัจจัยที่ละเอียดอ่อนที่ส่งผลต่อผลลัพธ์สุดท้าย
5 อันดับแอปพลิเคชั่นที่ใช้งานได้จริงของ Bayesian Networks
Bayesian Networks มีการใช้กันอย่างแพร่หลายในด้านวิทยาศาสตร์ข้อมูลเพื่อให้ได้ผลลัพธ์ที่แม่นยำพร้อมข้อมูลที่ไม่แน่นอน
แอพพลิเคชั่นของ Bayesian Networks
1. ตัวกรองสแปม
คุณต้องโกหกแน่ๆ ถ้าคุณบอกว่าคุณไม่เคยสงสัยเลยว่า Gmail กรองอีเมลขยะอย่างไร (อีเมลที่ไม่พึงประสงค์และไม่พึงประสงค์ โดยใช้ตัวกรองสแปม Bayesian ซึ่งเป็นตัวกรองที่มีประสิทธิภาพสูงสุด
2. รหัสเทอร์โบ
Bayesian Networks ใช้เพื่อสร้างรหัสเทอร์โบซึ่งเป็นรหัสแก้ไขข้อผิดพลาดที่ส่งต่อประสิทธิภาพสูง สิ่งเหล่านี้ใช้ในเครือข่ายมือถือ 3G และ 4G
3. การประมวลผลภาพ
Bayesian Networks ใช้การคำนวณทางคณิตศาสตร์เพื่อแปลงรูปภาพให้อยู่ในรูปแบบดิจิทัล นอกจากนี้ยังช่วยให้การปรับปรุงภาพ

4. การตรวจสอบทางชีวภาพ
การหาปริมาณความเข้มข้นของสารเคมีไม่สามารถทำได้ง่ายไปกว่านี้ด้วย Bayesian Networks ในสิ่งนี้ ปริมาณเลือดและเนื้อเยื่อในมนุษย์วัดโดยใช้ตัวชี้วัด
5. เครือข่ายการกำกับดูแลยีน (GNR)
GNR ประกอบด้วยส่วนดีเอ็นเอต่างๆ ของเซลล์ที่มีปฏิสัมพันธ์กับเนื้อหาของเซลล์อื่นๆ ผ่านผลิตภัณฑ์การแสดงออกของโปรตีนและอาร์เอ็นเอ การคาดการณ์พฤติกรรมสามารถวิเคราะห์ได้โดยใช้ Bayesian Networks
บทสรุป
ในบล็อกโพสต์ออนไลน์นี้ คุณได้เรียนรู้ว่า Bayesian Networks ช่วยให้เราได้รับผลลัพธ์ที่ถูกต้องจากข้อมูลที่มีอยู่ได้อย่างไร แม้แต่ข้อมูลที่มีความแปรผันเพียงเล็กน้อยก็อาจส่งผลกระทบอย่างมีนัยสำคัญต่อผลลัพธ์สุดท้าย Bayesian Networks ช่วยเราวิเคราะห์ข้อมูลโดยใช้สาเหตุแทนที่จะเป็นแค่ความสัมพันธ์
พวกเขาได้พิสูจน์แล้วว่าเป็นการปฏิวัติในสาขาวิทยาศาสตร์ข้อมูล เห็นได้ชัดว่าการประกอบอาชีพด้านวิทยาศาสตร์นี้สามารถช่วยให้คุณได้งานในฝัน ดังนั้น ลงทะเบียนหนึ่งในหลักสูตรของเราในด้านวิทยาศาสตร์ข้อมูลและเรียนรู้จากผู้เชี่ยวชาญ! นอกจากนี้เรายังให้การสนับสนุนด้านอาชีพฟรีจากที่ปรึกษาด้านอาชีพชั้นนำและมีประสบการณ์ ดาวน์โหลดโบรชัวร์เพื่อเรียนรู้เพิ่มเติมเกี่ยวกับหลักสูตร
หากคุณต้องการทราบข้อมูลเพิ่มเติมเกี่ยวกับอาชีพในแมชชีนเลิร์นนิงและปัญญาประดิษฐ์ โปรดดูที่ IIT Madras และการรับรองขั้นสูงของ upGrad ในการเรียนรู้ของเครื่องและคลาวด์
องค์ประกอบของเครือข่าย Bayesian คืออะไร?
Bayesian Networks มีต้นกำเนิดมาจากทฤษฎีบท Bayes ซึ่งตั้งชื่อตาม Thomas Bayes นักคณิตศาสตร์ชาวอังกฤษที่มีชื่อเสียง ทฤษฎีบทนี้เป็นสูตรทางคณิตศาสตร์ที่ใช้กำหนดความน่าจะเป็นแบบมีเงื่อนไข Bayesian Networks ในด้านปัญญาประดิษฐ์นั้นได้มาจาก Bayesian Statistics ซึ่งมีทฤษฎีบท Bayes เป็นเลเยอร์พื้นฐาน เครือข่ายแบบเบย์ประกอบด้วยสองโมดูล – ความน่าจะเป็นแบบมีเงื่อนไขในโมดูลเชิงปริมาณและกราฟวงจรกำกับทิศทางในโมดูลเชิงคุณภาพ ใน AI และแมชชีนเลิร์นนิง Bayesian Networks เป็นเครื่องมือที่ใช้สำหรับการให้เหตุผลและการสร้างแบบจำลองตามความเชื่อที่ไม่แน่นอน
คุณจำเป็นต้องรู้ความน่าจะเป็นและสถิติเท่าใดสำหรับการเรียนรู้ของเครื่อง
ส่วนสำคัญของ AI และสาขาย่อยที่แตกต่างกันนั้นขึ้นอยู่กับความน่าจะเป็นและสถิติ เมื่อพูดถึงแมชชีนเลิร์นนิง คุณต้องพิจารณาให้มากขึ้นว่าเป็นสาขาสหวิทยาการ ซึ่งใช้ความน่าจะเป็น สถิติ และอัลกอริทึมต่างๆ สถิติและความน่าจะเป็นเป็นสาขาที่เกี่ยวข้องกันของคณิตศาสตร์ที่ใช้ในการวิเคราะห์เหตุการณ์ที่เกี่ยวข้องกัน การรวมกันของสถิติ ความน่าจะเป็น และอัลกอริธึมนี้ ท้ายที่สุดแล้วจะใช้เพื่อสร้างแอปพลิเคชันอัจฉริยะที่เรียนรู้จากข้อมูลและยังให้ข้อมูลเชิงลึกอันมีค่าอีกด้วย ดังนั้น จำเป็นต้องมีความเข้าใจพื้นฐานเกี่ยวกับสถิติและความน่าจะเป็น หากคุณต้องการเรียนรู้แมชชีนเลิร์นนิง คุณควรทำความคุ้นเคยกับแนวคิดพื้นฐาน เช่น ความน่าจะเป็นเชิงประจักษ์และเชิงทฤษฎี ความน่าจะเป็นร่วมกัน ความน่าจะเป็นแบบมีเงื่อนไข ทฤษฎีบทเบย์ สถิติพรรณนา สถิติพรรณนาแบบตัวแปรเดียวและแบบสองตัวแปร สหสัมพันธ์ ฯลฯ
ข้อดีของการใช้ Bayesian Networks ใน AI คืออะไร?
Bayesian Networks เป็นเทคนิคที่ได้รับความนิยมอย่างมากสำหรับการสร้างแบบจำลองสำหรับโดเมนที่ซับซ้อนและไม่แน่นอน เมื่อใช้ Bayesian Networks คุณสามารถพัฒนากรอบงานเชิงตรรกะทางคณิตศาสตร์และแข็งแกร่งสำหรับภูมิประเทศที่ไม่แน่นอน เช่น ระบบนิเวศและการจัดการสิ่งแวดล้อม ข้อได้เปรียบที่สำคัญที่สุดของการใช้เทคนิคนี้คือ คุณสามารถรวมข้อมูลจากแหล่งที่ต่างกันและระดับความแม่นยำที่แตกต่างกันลงในแบบจำลองทางคณิตศาสตร์ที่เชื่อมโยงกันได้อย่างง่ายดาย ซึ่งจะช่วยรวมความรู้ของผู้เชี่ยวชาญเข้ากับข้อมูลเกี่ยวกับตัวแปรที่ไม่มีข้อมูล
