Bayessche Netze: Einführung, Beispiele und praktische Anwendungen
Veröffentlicht: 2020-02-23Alle, die schon einmal mit Daten oder Statistiken gearbeitet haben, wissen eines sicher: Korrelation bedeutet nicht unbedingt Kausalität. Auch wenn dies ziemlich offensichtlich klingen mag, könnte es Sie schockieren zu erfahren, dass die meisten Fehler in Daten aufgrund der Verwechslung der beiden Begriffe auftreten. Dies liegt vor allem daran, dass es zwar bequem ist, eine Korrelation zu definieren, es aber fast unmöglich ist, eine Kausalität zu definieren oder zu quantifizieren.
Tatsächlich stellt Judea Pearl, Autorin von Causality: Models, Reasoning, and Inference , in dem Buch fest, dass Menschen ihre mathematischen Bemühungen auf wahrscheinlichkeitstheoretische und statistische Schlussfolgerungen konzentrieren und kausale Überlegungen „der Gnade der Intuition und des guten Urteilsvermögens überlassen“. Er sagt, dass dies ein wesentlicher Faktor ist, dem wir in Bezug auf den wissenschaftlichen Fortschritt noch weit hinterherhinken.
Dies ist, wenn Bayesian Networks es uns leicht machen. Sie helfen uns, Korrelation von Kausalität zu unterscheiden, indem sie es uns ermöglichen, verschiedene unabhängige Ursachen gleichzeitig zu sehen. All dies wird genau durchgeführt, da maschinelle Lernalgorithmen nicht mit Subjektivität oder Intuition arbeiten; Sie arbeiten mit Daten.
Sehen wir uns ein Beispiel an, um zu verstehen, wie Bayes'sche Netzwerke funktionieren.
Inhaltsverzeichnis
Beispiel für Bayes'sche Netzwerke
Nehmen wir für dieses Beispiel an, dass die Welt von einer äußerst seltenen, aber tödlichen Krankheit heimgesucht wird; Angenommen, es besteht eine Wahrscheinlichkeit von 1 zu 1000, dass Sie mit der Krankheit infiziert sind.
Um herauszufinden, ob jemand an der Krankheit leidet, entwickeln Ärzte einen Test. Der Haken ist, dass es nur zu 99% genau ist.

Wie werden Sie sicher wissen, ob Sie die Krankheit haben oder nicht? Beeinflusst die Durchführung eines weiteren Tests die Ergebnisse?
Mal sehen, was passiert, wenn Sie dirigieren …
Prüfung 1
Da die Krankheit nur 1 von 1000 betrifft, beträgt die Wahrscheinlichkeit, dass Sie infiziert sind:
| Infiziert | 0,001 |
| Kostenlos | 0,999 |
Krankheit CPT (bedingte Wahrscheinlichkeitstabelle)
Genauso wie 1 von 1000 die Möglichkeit hat, an der Krankheit zu leiden, sind 999 von 1000 frei davon.
Auf ähnliche Weise erstellen wir eine Tabelle, um die Wahrscheinlichkeit des Tests zu berechnen. Wie bereits erwähnt, ist der Test nur zu 99% genau. Das bedeutet, dass das Ergebnis nur zu 99 % wahr ist. Ähnlich verhält es sich mit negativen Ergebnissen.
| Virenpräsenz | Infiziert | Kostenlos |
| Test 1 (positiv) | 0,99 | 0,01 |
| Test 1 (negativ) | 0,01 | 0,99 |
Test1 CPT (bedingte Wahrscheinlichkeitstabelle)
Lassen Sie uns nun ein Diagramm zeichnen, um zu sehen, wie das Vorhandensein der Krankheit von den Testergebnissen beeinflusst wird.
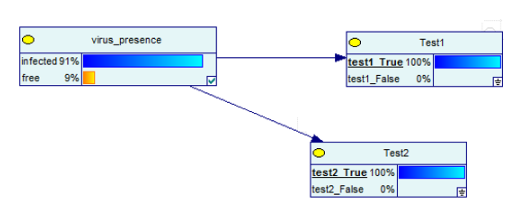
Wenn ich diese Zellen mit den Ergebnissen des Tests fülle, erhalte ich das folgende Ergebnis.

Bildquelle
Wie Sie sehen können, besteht bei einem positiven Testergebnis nur eine Wahrscheinlichkeit von 9 %, dass Sie an der Krankheit leiden.
Nun, wie sind wir an diese Nummer gekommen?
Satz von Bayes!
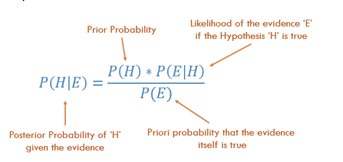
Bildquelle
In unserem Beispiel
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9 %
Was sagt uns das?
Selbst wenn der Test positiv ist, besteht aufgrund der Seltenheit der Krankheit nur eine Wahrscheinlichkeit von 9 %, an der Krankheit zu erkranken.
Was passiert also, wenn Sie sicherheitshalber einen weiteren Test machen und dieser auch positiv ausfällt?
Lesen Sie: Projektideen für maschinelles Lernen für Anfänger
Prüfung 2
Auch der zweite Test wird nur zu 99 % genau sein.
| Virenpräsenz | Infiziert | Kostenlos |
| Test 2 (positiv) | 0,99 | 0,01 |
| Test 2 (negativ) | 0,01 | 0,99 |
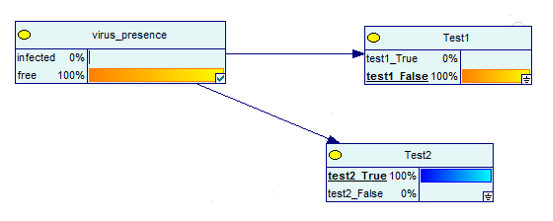
Das Bayessche Netzwerk wäre jetzt:
Bildquelle
Die Ergebnisse haben sich umgekehrt!
Das heißt, wenn Sie zwei positive Ergebnisse bei zwei Tests erhalten, steigt die Wahrscheinlichkeit, sich mit dem Virus zu infizieren, von 9 % auf 91 %. Aber auch hier heißt es nicht 100%!
Was ist nun, wenn Sie beim Test ein positives und ein negatives Ergebnis erhalten?
Bildquelle
Wie Sie sehen können, besteht eine 100-prozentige Chance, dass Sie die Krankheit nicht haben, falls einer der beiden Tests negativ ist.
Prüfung 3
Noch besser wird es, wenn Sie drei Tests durchführen und sich alle als wahr herausstellen.

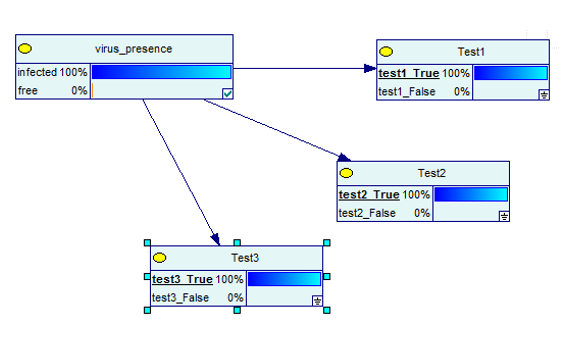
Bildquelle
Jetzt besteht eindeutig eine 100-prozentige Chance, dass Sie infiziert sind.
Mal sehen, was passiert, wenn einer der Tests negativ ist, aber die anderen beiden positiv sind.
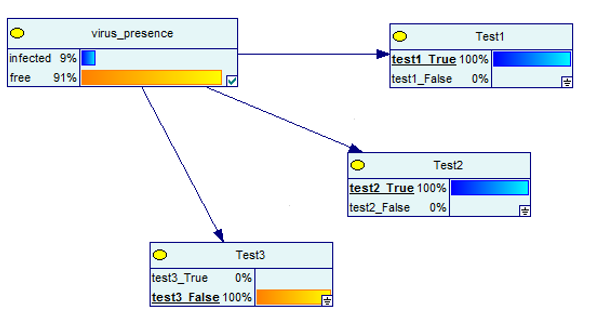
Bildquelle
Auch hier sind die Ergebnisse zu 91 % positiv für das Vorhandensein eines Virus.
Bayes'sche Netzwerke und Datenmodellierung
Im obigen Beispiel ist ersichtlich, dass Bayes'sche Netzwerke eine wichtige Rolle spielen, wenn es darum geht, Daten zu modellieren, um genaue Ergebnisse zu liefern.
Tatsächlich ermöglicht uns die Verfeinerung des Netzwerks durch Einbeziehung weiterer Faktoren, die das Ergebnis beeinflussen könnten, auch die Visualisierung und Simulation verschiedener Szenarien mithilfe von Bayes'schen Netzwerken.
Bayes'sche Netzwerke sind auch ein großartiges Werkzeug, um Unfairness in Daten zu quantifizieren und Techniken zu kuratieren, um diese Unfairness zu verringern.
In solchen Fällen ist es am besten, pfadspezifische Techniken zu verwenden, um sensible Faktoren zu identifizieren, die sich auf die Endergebnisse auswirken.
Top 5 praktische Anwendungen von Bayes'schen Netzwerken
Bayes'sche Netzwerke werden im Bereich der Datenwissenschaft häufig verwendet, um genaue Ergebnisse mit unsicheren Daten zu erhalten.
Anwendungen von Bayes'schen Netzen
1. Spamfilter
Sie müssen lügen, wenn Sie sagen, dass Sie sich nie gefragt haben, wie Gmail Spam-E-Mails (unerwünschte und unerwünschte E-Mails) filtert. Es verwendet den Bayes'schen Spam-Filter, der der robusteste Filter ist.
2. Turbo-Code
Bayes'sche Netzwerke werden verwendet, um Turbocodes zu erstellen, bei denen es sich um leistungsstarke Vorwärtsfehlerkorrekturcodes handelt. Diese werden in 3G- und 4G-Mobilfunknetzen verwendet.
3. Bildverarbeitung
Bayes'sche Netzwerke verwenden mathematische Operationen, um Bilder in ein digitales Format umzuwandeln. Es ermöglicht auch eine Bildverbesserung.

4. Biomonitoring
Die Quantifizierung der Konzentration von Chemikalien könnte nicht einfacher sein als mit Bayesian Networks. Dabei wird die Blut- und Gewebemenge des Menschen anhand von Indikatoren gemessen.
5. Genregulatorisches Netzwerk (GNR)
Ein GNR enthält verschiedene DNA-Segmente einer Zelle, die durch Protein- und RNA-Expressionsprodukte mit anderen Zellinhalten interagieren. Die Vorhersagen seines Verhaltens können mithilfe von Bayes'schen Netzwerken analysiert werden.
Fazit
In diesem Online-Blogbeitrag haben Sie erfahren, wie Bayes'sche Netzwerke uns helfen, genaue Ergebnisse aus den vorliegenden Daten zu erhalten. Selbst die geringfügigsten Abweichungen in den Daten können das Endergebnis erheblich beeinflussen. Bayes'sche Netzwerke helfen uns bei der Analyse von Daten mithilfe von Kausalität statt nur Korrelation.
Sie haben sich im Bereich Data Science als revolutionär erwiesen. Natürlich kann Ihnen eine Karriere in dieser Wissenschaft dabei helfen, Ihren Traumjob zu bekommen. Melden Sie sich also für einen unserer Kurse in Data Science an und lernen Sie von den Experten! Wir bieten auch kostenlose Karriereunterstützung durch erstklassige und erfahrene Karriereberater. Laden Sie die Broschüre herunter, um mehr über den Kurs zu erfahren.
Wenn Sie mehr über Karrieren in maschinellem Lernen und künstlicher Intelligenz erfahren möchten, lesen Sie die Advanced Certification in Machine Learning and Cloud von IIT Madras und upGrad.
Was sind die Komponenten eines Bayes'schen Netzes?
Bayes'sche Netze haben ihren Ursprung im Satz von Bayes, der nach dem berühmten britischen Mathematiker Thomas Bayes benannt ist. Dieser Satz ist im Wesentlichen eine mathematische Formel zur Bestimmung der bedingten Wahrscheinlichkeit. Bayes'sche Netzwerke im Bereich der künstlichen Intelligenz werden von der Bayes'schen Statistik abgeleitet, die das Bayes-Theorem als Grundlage hat. Ein Bayes'sches Netzwerk besteht aus zwei Modulen – der bedingten Wahrscheinlichkeit im quantitativen Modul und dem gerichteten azyklischen Graphen im qualitativen Modul. In der KI und beim maschinellen Lernen sind Bayes-Netzwerke Werkzeuge, die zum Denken und Modellieren auf der Grundlage unsicherer Überzeugungen verwendet werden.
Wie viel Wahrscheinlichkeit und Statistiken müssen Sie für maschinelles Lernen kennen?
Ein erheblicher Teil der KI und ihrer verschiedenen Teilgebiete basiert auf Wahrscheinlichkeit und Statistik. Wenn es um maschinelles Lernen geht, müssen Sie es eher als interdisziplinäres Gebiet betrachten, das Wahrscheinlichkeit, Statistik und verschiedene Algorithmen verwendet. Statistik und Wahrscheinlichkeit sind verwandte Bereiche der Mathematik, die zur Analyse des relativen Auftretens von Ereignissen verwendet werden. Diese Kombination aus Statistik, Wahrscheinlichkeit und Algorithmen wird letztendlich verwendet, um intelligente Anwendungen zu erstellen, die aus Daten lernen und auch wertvolle Erkenntnisse bieten. Ein grundlegendes Verständnis von Statistik und Wahrscheinlichkeit ist also zwingend erforderlich, wenn Sie maschinelles Lernen lernen möchten. Sie sollten mit grundlegenden Konzepten wie empirischer und theoretischer Wahrscheinlichkeit, gemeinsamer Wahrscheinlichkeit, bedingter Wahrscheinlichkeit, Satz von Bayes, deskriptiver Statistik, univariater und bivariater deskriptiver Statistik, Korrelation usw. vertraut sein.
Was sind die Vorteile der Verwendung von Bayes'schen Netzwerken in der KI?
Bayes'sche Netzwerke sind eine äußerst beliebte Technik zum Erstellen von Modellen für komplexe und unsichere Domänen. Mit Bayes'schen Netzwerken können Sie einen mathematisch logischen und robusten Rahmen für unsichere Landschaften wie Ökosysteme und Umweltmanagement entwickeln. Der wichtigste Vorteil bei der Verwendung dieser Technik besteht darin, dass Sie Daten aus heterogenen Quellen und unterschiedlichen Genauigkeitsstufen problemlos in ein mathematisch kohärentes Modell integrieren können. Dies hilft, Expertenwissen mit Daten über Variablen zu kombinieren, die keine Daten enthalten.
