Réseaux Bayésiens : Introduction, Exemples et Applications Pratiques
Publié: 2020-02-23Tous ceux qui ont déjà travaillé avec des données ou des statistiques savent une chose avec certitude : la corrélation ne signifie pas nécessairement ou n'implique pas nécessairement la causalité. Maintenant, bien que cela puisse sembler assez évident, cela pourrait vous choquer d'apprendre que la plupart des erreurs dans les données se produisent à cause de la confusion entre les deux termes. C'est principalement parce que s'il est pratique de définir la corrélation, il est presque impossible de définir ou de quantifier la causalité.
En fait, Judea Pearl, auteur de Causality: Models, Reasoning, and Inference , déclare dans le livre que les humains concentrent leurs efforts mathématiques sur les inférences probabilistes et statistiques, laissant les considérations causales "à la merci de l'intuition et du bon jugement". Il dit que c'est un facteur majeur que nous accusons encore beaucoup de retard en termes de progrès scientifique.
C'est à ce moment que les réseaux bayésiens nous facilitent la tâche. Ils nous aident à distinguer la corrélation de la causalité en nous permettant de voir plusieurs causes indépendantes à la fois. Tout cela est fait avec précision car les algorithmes d'apprentissage automatique ne fonctionnent pas sur la subjectivité ou l'intuition ; ils travaillent sur des données.
Voyons un exemple pour comprendre comment fonctionnent les réseaux bayésiens.
Table des matières
Exemple de réseaux bayésiens
Pour cet exemple, supposons que le monde soit frappé par une maladie extrêmement rare mais mortelle ; disons qu'il y a 1 chance sur 1000 que vous soyez infecté par la maladie.
Maintenant, pour déterminer si quelqu'un souffre de la maladie, les médecins développent un test. Le hic, c'est qu'il n'est précis qu'à 99%.

Comment saurez-vous avec certitude si vous avez la maladie ou non? Passer un autre test affectera-t-il les résultats ?
Voyons ce qui se passe lorsque vous conduisez…
Essai 1
Comme la maladie ne touche qu'1 personne sur 1000, la probabilité que vous soyez infecté est de :
| Infecté | 0,001 |
| Gratuit | 0,999 |
Maladie CPT (table de probabilité conditionnelle)
De toute évidence, tout comme 1 sur 1000 a une chance de souffrir de la maladie, 999 sur 1000 en sont exempts.
De même, nous allons créer un tableau pour calculer la probabilité du test. Comme mentionné précédemment, si le test n'est précis qu'à 99%. Cela signifie qu'il n'y a que 99 % de chances que le résultat soit vrai. Similaire est le cas avec des résultats négatifs.
| Présence de virus | Infecté | Gratuit |
| Essai 1 (Positif) | 0,99 | 0,01 |
| Essai 1 (négatif) | 0,01 | 0,99 |
Test1 CPT (table de probabilité conditionnelle)
Maintenant, traçons un graphique pour voir comment la présence de la maladie est affectée par les résultats du test.
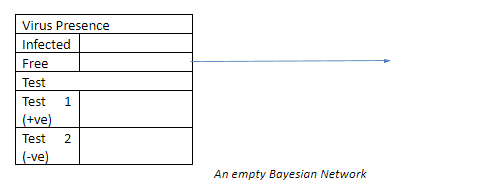
Remplir ces cellules avec les résultats du test me donnera le résultat suivant.

Source des images
Comme vous pouvez le constater, si le test s'avère positif, il n'y a que 9 % de chances que vous souffriez de la maladie.
Maintenant, comment avons-nous obtenu ce numéro ?
Théorème de Bayes !
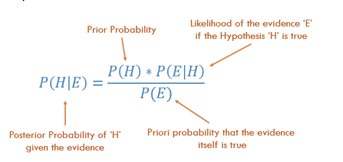
Source des images
Dans notre exemple,
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9 %
Qu'est-ce que cela nous dit?
Même lorsque le test est positif, en raison de la rareté de la maladie, il n'y a que 9% de chances d'avoir la maladie.
Alors, que se passe-t-il lorsque vous faites un autre test pour être sûr et que celui-ci s'avère également positif.
Lire : Idées de projets d'apprentissage automatique pour les débutants
Essai 2
Encore une fois, le deuxième test ne sera également précis qu'à 99%.
| Présence de virus | Infecté | Gratuit |
| Test 2 (Positif) | 0,99 | 0,01 |
| Test 2 (négatif) | 0,01 | 0,99 |
Le réseau bayésien serait maintenant :
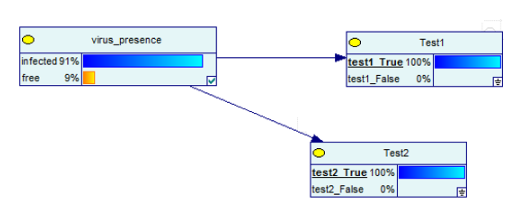
Source des images
Les résultats se sont inversés !
Cela signifie que si vous obtenez deux résultats positifs sur deux tests, les chances d'être infecté par le virus augmentent de 9 % à 91 %. Mais encore une fois, ça ne dit pas 100% !
Maintenant, que se passe-t-il si vous obtenez un résultat positif et un résultat négatif du test ?
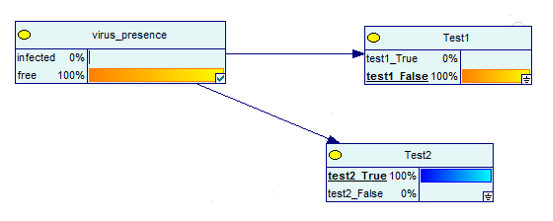
Source des images
Comme vous pouvez le constater, il y a 100 % de chances que vous n'ayez pas la maladie si l'un des deux tests est négatif.
Essai 3
Cela devient encore meilleur lorsque vous effectuez trois tests et qu'ils se révèlent tous vrais.
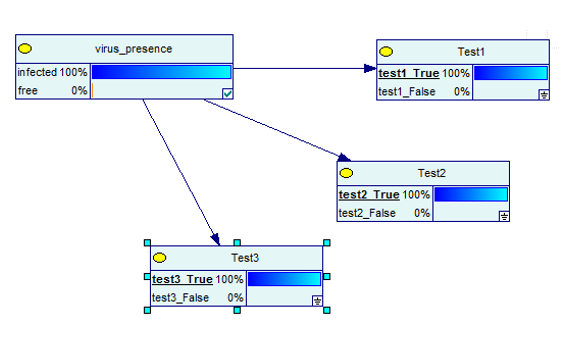

Source des images
De toute évidence, maintenant, il y a 100% de chances que vous soyez infecté.
Voyons maintenant ce qui se passe lorsque l'un des tests est négatif mais que les deux autres sont positifs.
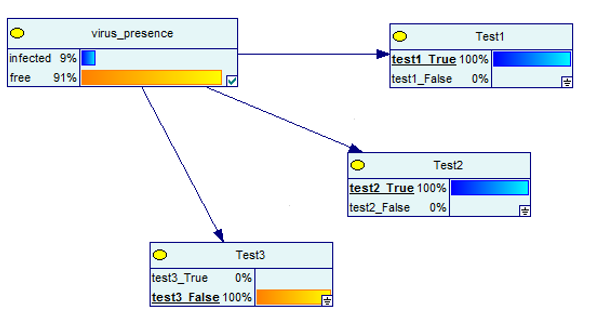
Source des images
Encore une fois, les résultats sont positifs à 91% pour la présence d'un virus.
Réseaux bayésiens et modélisation des données
Dans l'exemple ci-dessus, on peut voir que les réseaux bayésiens jouent un rôle important lorsqu'il s'agit de modéliser des données pour fournir des résultats précis.
En fait, affiner le réseau en incluant davantage de facteurs susceptibles d'affecter le résultat nous permet également de visualiser et de simuler différents scénarios à l'aide de réseaux bayésiens.
Les réseaux bayésiens sont également un excellent outil pour quantifier l'iniquité des données et organiser des techniques pour réduire cette iniquité.
Dans de tels cas, il est préférable d'utiliser des techniques spécifiques au chemin pour identifier les facteurs sensibles qui affectent les résultats finaux.
Top 5 des applications pratiques des réseaux bayésiens
Les réseaux bayésiens sont largement utilisés dans le domaine de la science des données pour obtenir des résultats précis avec des données incertaines.
Applications des réseaux bayésiens
1. Filtre anti-spam
Vous devez mentir si vous dites que vous ne vous êtes jamais demandé comment Gmail filtre les spams (e-mails indésirables et non sollicités). Il utilise le filtre anti-spam bayésien, qui est le filtre le plus robuste.
2. Code turbo
Les réseaux bayésiens sont utilisés pour créer des codes turbo qui sont des codes de correction d'erreur directe hautes performances. Ceux-ci sont utilisés dans les réseaux mobiles 3G et 4G.
3. Traitement des images
Les réseaux bayésiens utilisent des opérations mathématiques pour convertir les images au format numérique. Il permet également l'amélioration de l'image.

4. Biosurveillance
La quantification de la concentration de produits chimiques ne pourrait pas être plus simple qu'avec les réseaux bayésiens. En cela, la quantité de sang et de tissus chez l'homme est mesurée à l'aide d'indicateurs.
5. Réseau de réglementation des gènes (GNR)
Un GNR contient divers segments d'ADN d'une cellule qui interagissent avec d'autres contenus cellulaires par le biais de produits d'expression de protéines et d'ARN. Les prédictions de son comportement peuvent être analysées à l'aide de réseaux bayésiens.
Conclusion
Dans cet article de blog en ligne, vous avez appris comment les réseaux bayésiens nous aident à obtenir des résultats précis à partir des données disponibles. Même les plus petites variations dans les données peuvent affecter de manière significative le résultat final. Les réseaux bayésiens nous aident à analyser les données en utilisant la causalité au lieu de la simple corrélation.
Ils se sont avérés révolutionnaires dans le domaine de la science des données. De toute évidence, entreprendre une carrière dans cette science peut vous aider à obtenir l'emploi de vos rêves. Alors, inscrivez-vous à l'un de nos cours en science des données et apprenez des experts ! Nous offrons également un soutien professionnel gratuit par des conseillers d'orientation de premier ordre et expérimentés. Téléchargez la brochure pour en savoir plus sur le cours.
Si vous souhaitez en savoir plus sur les carrières dans l'apprentissage automatique et l'intelligence artificielle, consultez IIT Madras et la certification avancée d'upGrad en apprentissage automatique et cloud.
Quels sont les composants d'un réseau bayésien ?
Les réseaux bayésiens trouvent leur origine dans le théorème de Bayes, qui porte le nom de Thomas Bayes, le célèbre mathématicien britannique. Ce théorème est essentiellement une formule mathématique utilisée pour déterminer la probabilité conditionnelle. Les réseaux bayésiens dans le domaine de l'intelligence artificielle sont dérivés des statistiques bayésiennes, qui ont le théorème de Bayes comme couche fondamentale. Un réseau bayésien se compose de deux modules - la probabilité conditionnelle dans le module quantitatif et le graphe acyclique dirigé dans son module qualitatif. Dans l'IA et l'apprentissage automatique, les réseaux bayésiens sont des outils utilisés pour le raisonnement et la modélisation basés sur des croyances incertaines.
De combien de probabilités et de statistiques avez-vous besoin pour l'apprentissage automatique ?
Une partie considérable de l'IA et de ses différents sous-domaines est basée sur la probabilité et les statistiques. En ce qui concerne l'apprentissage automatique, vous devez le considérer davantage comme un domaine interdisciplinaire, qui utilise des probabilités, des statistiques et divers algorithmes. Les statistiques et les probabilités sont des domaines mathématiques connexes utilisés pour analyser l'occurrence relative d'événements. Cette combinaison de statistiques, de probabilités et d'algorithmes est finalement utilisée pour créer des applications intelligentes qui apprennent à partir des données et offrent également des informations précieuses. Ainsi, une compréhension de base des statistiques et des probabilités est obligatoire si vous souhaitez apprendre l'apprentissage automatique. Vous devez être familiarisé avec les concepts fondamentaux tels que la probabilité empirique et théorique, la probabilité conjointe, la probabilité conditionnelle, le théorème de Bayes, les statistiques descriptives, les statistiques descriptives univariées et bivariées, la corrélation, etc.
Quels sont les avantages de l'utilisation des réseaux bayésiens en IA ?
Les réseaux bayésiens sont une technique extrêmement populaire pour créer des modèles pour des domaines complexes et incertains. En utilisant les réseaux bayésiens, vous pouvez développer un cadre mathématiquement logique et robuste pour des paysages incertains comme les écosystèmes et la gestion de l'environnement. L'avantage le plus important de l'utilisation de cette technique est que vous pouvez facilement incorporer des données provenant de sources hétérogènes et de niveaux de précision variables dans un modèle mathématiquement cohérent. Cela permet de combiner les connaissances d'experts avec des données sur des variables qui n'ont pas de données.
