Bayesian Networks: Pengenalan, Contoh dan Aplikasi Praktis
Diterbitkan: 2020-02-23Semua orang yang pernah bekerja dengan data atau statistik mengetahui satu hal dengan pasti: korelasi tidak selalu berarti atau menyiratkan sebab-akibat. Sekarang, meskipun ini mungkin terdengar cukup jelas, Anda mungkin terkejut mengetahui bahwa sebagian besar kesalahan dalam data terjadi karena kebingungan antara kedua istilah tersebut. Hal ini terutama karena meskipun mudah untuk mendefinisikan korelasi, hampir tidak mungkin untuk mendefinisikan atau mengukur sebab-akibat.
Faktanya, Judea Pearl, penulis Causality: Models, Reasoning, and Inference , menyatakan dalam buku itu bahwa manusia memfokuskan upaya matematis mereka pada inferensi probabilistik dan statistik, meninggalkan pertimbangan kausal "untuk belas kasihan intuisi dan penilaian yang baik." Dia mengatakan bahwa ini adalah faktor utama bahwa kita masih sangat tertinggal dalam hal kemajuan ilmiah.
Saat inilah Bayesian Networks memudahkan kami. Mereka membantu kita membedakan korelasi dari sebab-akibat dengan memungkinkan kita untuk melihat berbagai penyebab independen sekaligus. Semua ini dilakukan secara akurat karena algoritme pembelajaran mesin tidak bekerja berdasarkan subjektivitas atau intuisi; mereka bekerja pada data.
Mari kita lihat contoh untuk memahami bagaimana Bayesian Networks beroperasi.
Daftar isi
Contoh Jaringan Bayesian
Demi contoh ini, mari kita anggap bahwa dunia sedang dilanda penyakit yang sangat langka namun mematikan; katakanlah ada kemungkinan 1 dari 1000 bahwa Anda terinfeksi oleh penyakit ini.
Sekarang, untuk mengetahui apakah seseorang menderita penyakit tersebut, dokter mengembangkan tes. Tangkapannya adalah hanya 99% akurat.

Bagaimana cara mengetahui dengan pasti apakah Anda mengidap penyakit tersebut atau tidak? Apakah mengikuti tes lain akan memengaruhi hasil?
Mari kita lihat apa yang terjadi ketika Anda melakukan…
Tes 1
Karena penyakit ini hanya mempengaruhi 1 dari 1000, kemungkinan Anda terinfeksi adalah:
| Terjangkit | 0,001 |
| Gratis | 0,999 |
Penyakit CPT (Tabel Probabilitas Bersyarat)
Jelas, seperti halnya 1 dari 1000 memiliki kemungkinan menderita penyakit, 999 dari 1000 bebas darinya.
Demikian pula, kami akan membuat tabel untuk menghitung probabilitas tes. Seperti yang disebutkan sebelumnya, jika tes di hanya 99% akurat. Itu berarti hanya ada 99% kemungkinan bahwa hasilnya benar. Demikian pula halnya dengan hasil negatif.
| Kehadiran Virus | Terjangkit | Gratis |
| Tes 1 (Positif) | 0,99 | 0,01 |
| Tes 1 (Negatif) | 0,01 | 0,99 |
Test1 CPT (Tabel Probabilitas Bersyarat)
Sekarang, mari kita buat grafik untuk melihat bagaimana keberadaan penyakit dipengaruhi oleh hasil tes.
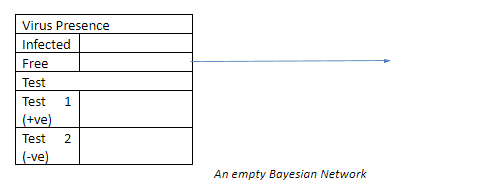
Mengisi sel-sel ini dengan hasil tes akan memberi saya hasil berikut.

Sumber gambar
Seperti yang Anda lihat, jika tesnya positif, hanya ada 9% kemungkinan Anda menderita penyakit tersebut.
Sekarang, bagaimana kita mendapatkan nomor ini?
Teorema Bayes!
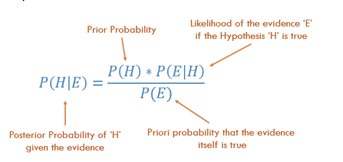
Sumber gambar
Dalam contoh kita,
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9%
Apa ini memberitahu kita?
Bahkan ketika tesnya positif, karena penyakitnya langka, hanya ada 9% kemungkinan mengidap penyakit itu.
Jadi, lalu, apa yang terjadi ketika Anda melakukan tes lain untuk memastikan dan ternyata hasilnya juga positif.
Baca: Ide Proyek Pembelajaran Mesin untuk Pemula
Tes 2
Sekali lagi, tes kedua juga hanya akan menjadi 99% akurat.
| Kehadiran Virus | Terjangkit | Gratis |
| Tes 2 (Positif) | 0,99 | 0,01 |
| Tes 2 (Negatif) | 0,01 | 0,99 |
Jaringan Bayesian sekarang akan menjadi:
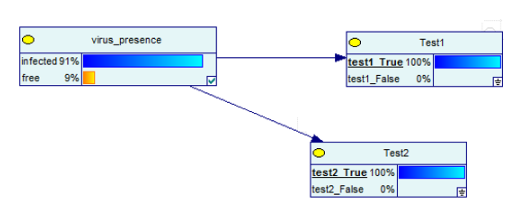
Sumber gambar
Hasilnya terbalik!
Artinya, jika Anda mendapatkan dua hasil positif pada dua tes, kemungkinan terinfeksi virus meningkat dari 9% menjadi 91%. Tapi sekali lagi, itu tidak mengatakan 100%!
Sekarang, bagaimana jika Anda mendapatkan satu hasil positif dan satu negatif dari tes?
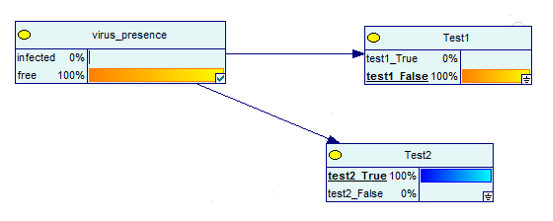
Sumber gambar
Seperti yang Anda lihat, ada kemungkinan 100% bahwa Anda tidak memiliki penyakit jika salah satu dari dua tes negatif.

Tes 3
Itu menjadi lebih baik ketika Anda melakukan tiga tes dan semuanya menjadi kenyataan.
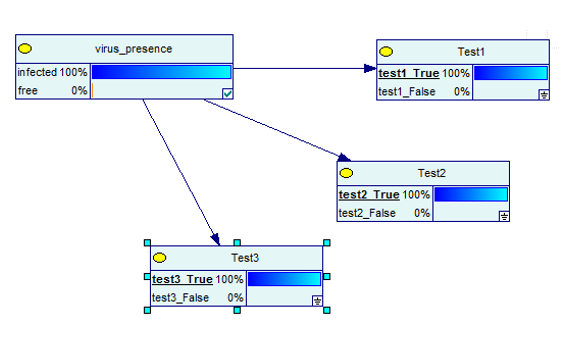
Sumber gambar
Jelas, sekarang, ada kemungkinan 100% bahwa Anda terinfeksi.
Sekarang mari kita lihat apa yang terjadi ketika salah satu tes negatif tetapi dua lainnya positif.
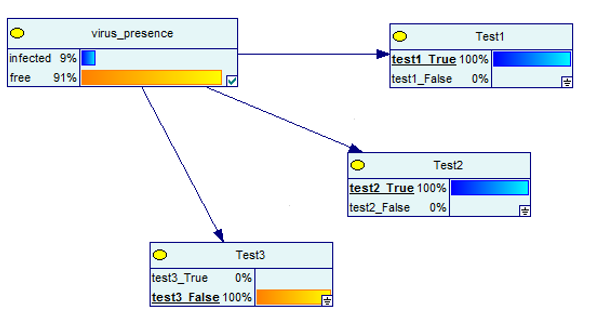
Sumber gambar
Sekali lagi, hasilnya 91% positif adanya virus.
Jaringan Bayesian dan Pemodelan Data
Pada contoh di atas, dapat dilihat bahwa Bayesian Networks memainkan peran penting dalam hal pemodelan data untuk memberikan hasil yang akurat.
Faktanya, menyempurnakan jaringan dengan memasukkan lebih banyak faktor yang mungkin memengaruhi hasil juga memungkinkan kami untuk memvisualisasikan dan mensimulasikan berbagai skenario menggunakan Bayesian Networks.
Bayesian Networks juga merupakan alat yang hebat untuk mengukur ketidakadilan dalam data dan teknik kurasi untuk mengurangi ketidakadilan ini.
Dalam kasus seperti itu, yang terbaik adalah menggunakan teknik khusus jalur untuk mengidentifikasi faktor sensitif yang memengaruhi hasil akhir.
5 Aplikasi Praktis Jaringan Bayesian Teratas
Bayesian Networks banyak digunakan di bidang ilmu data untuk mendapatkan hasil yang akurat dengan data yang tidak pasti.
Aplikasi Jaringan Bayesian
1. Filter Spam
Anda pasti berbohong jika mengatakan bahwa Anda tidak pernah bertanya-tanya bagaimana Gmail memfilter email spam (email yang tidak diinginkan dan tidak diminta. Ini menggunakan filter spam Bayesian, yang merupakan filter paling kuat.
2. Kode Turbo
Bayesian Networks digunakan untuk membuat kode turbo yang merupakan kode koreksi kesalahan maju berperforma tinggi. Ini digunakan dalam jaringan seluler 3G dan 4G.
3. Pemrosesan Gambar
Bayesian Networks menggunakan operasi matematika untuk mengubah gambar menjadi format digital. Ini juga memungkinkan peningkatan gambar.

4. Biomonitoring
Mengukur konsentrasi bahan kimia tidak bisa lebih mudah daripada dengan Bayesian Networks. Dalam hal ini, jumlah darah dan jaringan pada manusia diukur dengan menggunakan indikator.
5. Jaringan Pengatur Gen (GNR)
GNR berisi berbagai segmen DNA sel yang berinteraksi dengan isi sel lain melalui protein dan produk ekspresi RNA. Prediksi perilakunya dapat dianalisis menggunakan Bayesian Networks.
Kesimpulan
Dalam posting blog online ini, Anda mempelajari tentang bagaimana Bayesian Networks membantu kami mendapatkan hasil yang akurat dari data yang ada. Bahkan variasi kecil dalam data dapat secara signifikan mempengaruhi hasil akhir. Bayesian Networks membantu kami menganalisis data menggunakan sebab-akibat, bukan hanya korelasi.
Mereka telah terbukti revolusioner di bidang ilmu data. Jelas, mengambil karir dalam ilmu ini dapat membantu Anda mendapatkan pekerjaan impian Anda. Jadi, daftarkan diri Anda di salah satu kursus kami dalam ilmu data dan pelajari dari para ahlinya! Kami juga menawarkan dukungan karir gratis dari konselor karir terkemuka dan berpengalaman. Unduh brosur untuk mempelajari lebih lanjut tentang kursus ini.
Jika Anda ingin tahu lebih banyak tentang karier di Pembelajaran Mesin dan Kecerdasan Buatan, lihat IIT Madras dan Sertifikasi Lanjutan upGrad dalam Pembelajaran Mesin dan Cloud.
Apa saja komponen jaringan Bayesian?
Bayesian Networks berasal dari Teorema Bayes, yang dinamai dari Thomas Bayes, ahli matematika Inggris yang terkenal. Teorema ini pada dasarnya adalah rumus matematika yang digunakan untuk menentukan probabilitas bersyarat. Bayesian Networks di bidang kecerdasan buatan berasal dari Bayesian Statistics, yang memiliki Teorema Bayes sebagai lapisan dasarnya. Jaringan Bayesian terdiri dari dua modul – probabilitas bersyarat dalam modul kuantitatif dan grafik asiklik terarah dalam modul kualitatifnya. Dalam AI dan pembelajaran mesin, Bayesian Networks adalah alat yang digunakan untuk penalaran dan pemodelan berdasarkan keyakinan yang tidak pasti.
Berapa probabilitas dan statistik yang perlu Anda ketahui untuk pembelajaran mesin?
Sebagian besar AI dan subbidangnya yang berbeda didasarkan pada probabilitas dan statistik. Ketika berbicara tentang pembelajaran mesin, Anda perlu mempertimbangkannya lebih sebagai bidang interdisipliner, yang menggunakan probabilitas, statistik, dan berbagai algoritme. Statistik dan probabilitas adalah bidang matematika yang terkait yang digunakan untuk menganalisis kejadian relatif dari suatu peristiwa. Kombinasi statistik, probabilitas, dan algoritme ini pada akhirnya digunakan untuk membangun aplikasi cerdas yang belajar dari data dan juga menawarkan wawasan yang berharga. Jadi, pemahaman dasar tentang statistik dan probabilitas adalah wajib jika Anda ingin mempelajari pembelajaran mesin. Anda harus terbiasa dengan konsep dasar seperti probabilitas empiris dan teoretis, probabilitas gabungan, probabilitas bersyarat, Teorema Bayes, statistik deskriptif, statistik deskriptif univariat dan bivariat, korelasi, dll.
Apa keuntungan menggunakan Bayesian Networks di AI?
Bayesian Networks adalah teknik yang sangat populer untuk membuat model untuk domain yang kompleks dan tidak pasti. Dengan menggunakan Bayesian Networks, Anda dapat mengembangkan kerangka kerja yang logis dan kuat secara matematis untuk lanskap yang tidak pasti seperti ekosistem dan pengelolaan lingkungan. Keuntungan paling signifikan menggunakan teknik ini adalah Anda dapat dengan mudah menggabungkan data dari sumber yang heterogen dan tingkat akurasi yang bervariasi ke dalam model yang koheren secara matematis. Ini membantu menggabungkan pengetahuan ahli dengan data tentang variabel yang tidak memiliki data apa pun.
