Байесовские сети: введение, примеры и практическое применение
Опубликовано: 2020-02-23Все те, кто когда-либо работал с данными или статистикой, точно знают одно: корреляция не обязательно означает или подразумевает причинно-следственную связь. Теперь, хотя это может показаться довольно очевидным, вы можете быть шокированы, узнав, что большинство ошибок в данных происходит из-за путаницы между двумя терминами. Это в первую очередь потому, что, хотя определить корреляцию удобно, практически невозможно определить или количественно определить причинно-следственную связь.
На самом деле Джуда Перл, автор книги « Причинность: модели, рассуждения и выводы », утверждает в книге, что люди сосредотачивают свои математические усилия на вероятностных и статистических выводах, оставляя причинно-следственные связи «на милость интуиции и здравого смысла». Он говорит, что это основной фактор, от которого мы все еще сильно отстаем с точки зрения научного прогресса.
Это когда байесовские сети облегчают нам задачу. Они помогают нам отличить корреляцию от причинно-следственной связи, позволяя нам одновременно видеть различные независимые причины. Все это делается аккуратно, так как алгоритмы машинного обучения не работают на субъективности или интуиции; они работают с данными.
Давайте посмотрим на пример, чтобы понять, как работают байесовские сети.
Оглавление
Пример байесовских сетей
Ради этого примера предположим, что мир поражен чрезвычайно редкой, но смертельной болезнью; скажем, есть 1 из 1000 шансов, что вы заражены этой болезнью.
Теперь, чтобы выяснить, страдает ли кто-то этим заболеванием, врачи разрабатывают тест. Загвоздка в том, что точность всего 99%.

Как узнать наверняка, есть ли у вас заболевание или нет? Повлияет ли повторный тест на результаты?
Давайте посмотрим, что происходит, когда вы проводите…
Тест 1
Поскольку заболевание поражает только 1 человека из 1000, вероятность того, что вы заразитесь, составляет:
| Зараженный | 0,001 |
| Бесплатно | 0,999 |
CPT болезни (таблица условной вероятности)
Ясно, что как 1 из 1000 имеет шанс заболеть, так и 999 из 1000 свободны от него.
Точно так же мы создадим таблицу для расчета вероятности теста. Как упоминалось ранее, если тест точен только на 99%. Это означает, что вероятность того, что результат верен, составляет всего 99%. Аналогично и с отрицательными результатами.
| Наличие вируса | Зараженный | Бесплатно |
| Тест 1 (положительный) | 0,99 | 0,01 |
| Тест 1 (отрицательный) | 0,01 | 0,99 |
Test1 CPT (таблица условной вероятности)
Теперь построим график, чтобы увидеть, как на наличие болезни влияют результаты анализов.
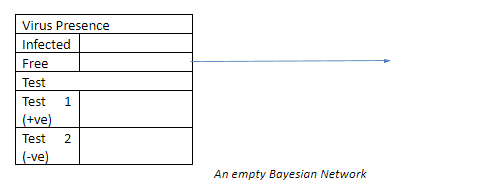
Заполнение этих ячеек результатами теста даст мне следующий результат.

Источник изображения
Как видите, если тест окажется положительным, вероятность того, что вы страдаете этим заболеванием, составляет всего 9%.
Теперь, как мы получили это число?
Теорема Байеса!
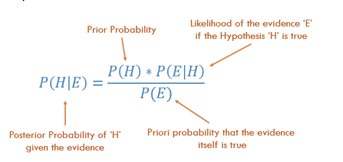
Источник изображения
В нашем примере
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 х 0,001) / (0,001 х 0,99 + 0,999 х 0,01) = 0,9 = 9%
Что это говорит нам?
Даже когда тест положительный, из-за того, что заболевание редкое, вероятность заболевания составляет всего 9%.
Итак, что происходит, когда вы делаете еще один тест, чтобы быть уверенным, и он тоже оказывается положительным.
Читайте: Идеи проекта машинного обучения для начинающих
Тест 2
Опять же, второй тест также будет точен только на 99%.
| Наличие вируса | Зараженный | Бесплатно |
| Тест 2 (положительный) | 0,99 | 0,01 |
| Тест 2 (отрицательный) | 0,01 | 0,99 |
Байесовская сеть теперь будет:
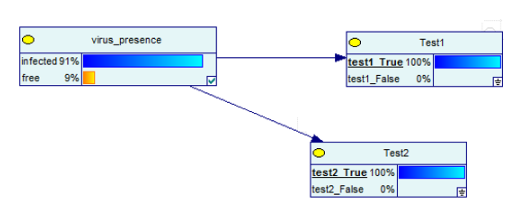
Источник изображения
Результаты изменились!
Это означает, что если вы получите два положительных результата на двух тестах, шансы заразиться вирусом увеличиваются с 9% до 91%. Но опять же, это не говорит о 100%!
А что, если вы получите один положительный и один отрицательный результат теста?
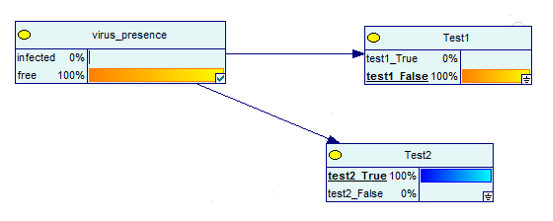
Источник изображения
Как видите, есть 100% вероятность того, что у вас нет заболевания, если один из двух тестов будет отрицательным.
Тест 3
Будет еще лучше, если вы проведете три теста, и все они окажутся верными.

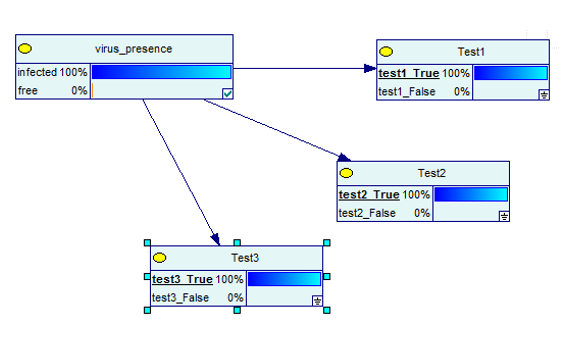
Источник изображения
Понятно, что теперь есть 100% вероятность того, что вы заражены.
Теперь давайте посмотрим, что происходит, когда один из тестов отрицательный, а два других положительные.
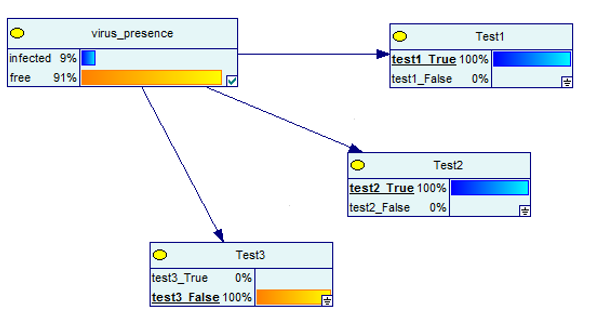
Источник изображения
Опять же, результаты 91% положительны на наличие вируса.
Байесовские сети и моделирование данных
В приведенном выше примере видно, что байесовские сети играют важную роль, когда речь идет о моделировании данных для получения точных результатов.
Фактически, уточнение сети путем включения большего количества факторов, которые могут повлиять на результат, также позволяет нам визуализировать и моделировать различные сценарии с использованием байесовских сетей.
Байесовские сети также являются отличным инструментом для количественной оценки несправедливости в данных и выбора методов для уменьшения этой несправедливости.
В таких случаях лучше всего использовать методы, специфичные для пути, для выявления чувствительных факторов, влияющих на конечные результаты.
5 лучших практических применений байесовских сетей
Байесовские сети широко используются в области науки о данных для получения точных результатов с неопределенными данными.
Приложения байесовских сетей
1. Спам-фильтр
Вы, должно быть, лжете, если говорите, что никогда не задумывались, как Gmail фильтрует спам (нежелательные и нежелательные электронные письма). Он использует байесовский спам-фильтр, который является самым надежным фильтром.
2. Турбо-код
Байесовские сети используются для создания турбокодов, которые представляют собой высокопроизводительные коды прямого исправления ошибок. Они используются в мобильных сетях 3G и 4G.
3. Обработка изображений
Байесовские сети используют математические операции для преобразования изображений в цифровой формат. Это также позволяет улучшить изображение.

4. Биомониторинг
Количественная оценка концентрации химических веществ не может быть проще, чем с помощью байесовских сетей. При этом количество крови и тканей у человека измеряют с помощью индикаторов.
5. Сеть регуляции генов (GNR)
GNR содержит различные сегменты ДНК клетки, которые взаимодействуют с другим содержимым клетки через продукты экспрессии белков и РНК. Прогнозы его поведения можно анализировать с помощью байесовских сетей.
Заключение
В этом сообщении в онлайн-блоге вы узнали о том, как байесовские сети помогают нам получать точные результаты из имеющихся данных. Даже небольшие различия в данных могут существенно повлиять на конечный результат. Байесовские сети помогают нам анализировать данные, используя причинно-следственную связь, а не только корреляцию.
Они оказались революционными в области науки о данных. Очевидно, что карьера в этой области науки может помочь вам получить работу своей мечты. Итак, запишитесь на один из наших курсов по науке о данных и учитесь у экспертов! Мы также предлагаем бесплатную поддержку карьеры от первоклассных и опытных консультантов по вопросам карьеры. Загрузите брошюру, чтобы узнать больше о курсе.
Если вы хотите узнать больше о карьере в области машинного обучения и искусственного интеллекта, ознакомьтесь с IIT Madras и расширенной сертификацией upGrad в области машинного обучения и облачных вычислений.
Из каких компонентов состоит байесовская сеть?
Байесовские сети берут свое начало в теореме Байеса, названной в честь Томаса Байеса, известного британского математика. Эта теорема по существу представляет собой математическую формулу, используемую для определения условной вероятности. Байесовские сети в области искусственного интеллекта основаны на байесовской статистике, фундаментальным слоем которой является теорема Байеса. Байесовская сеть состоит из двух модулей – условной вероятности в количественном модуле и ориентированного ациклического графа в качественном модуле. В искусственном интеллекте и машинном обучении байесовские сети — это инструменты, используемые для рассуждений и моделирования на основе неопределенных убеждений.
Сколько вероятности и статистики вам нужно знать для машинного обучения?
Значительная часть ИИ и его различных подполей основана на вероятности и статистике. Когда дело доходит до машинного обучения, нужно рассматривать его больше как междисциплинарную область, в которой используются вероятности, статистика и различные алгоритмы. Статистика и вероятность — это связанные области математики, используемые для анализа относительного возникновения событий. Эта комбинация статистики, вероятности и алгоритмов в конечном итоге используется для создания интеллектуальных приложений, которые извлекают уроки из данных, а также предлагают ценную информацию. Таким образом, базовое понимание статистики и вероятности является обязательным, если вы хотите изучить машинное обучение. Вы должны быть знакомы с такими основополагающими понятиями, как эмпирическая и теоретическая вероятность, совместная вероятность, условная вероятность, теорема Байеса, описательная статистика, одномерная и двумерная описательная статистика, корреляция и т. д.
Каковы преимущества использования байесовских сетей в ИИ?
Байесовские сети — чрезвычайно популярный метод создания моделей для сложных и неопределенных областей. Используя байесовские сети, вы можете разработать математически логическую и надежную основу для неопределенных ландшафтов, таких как экосистемы и управление окружающей средой. Наиболее значительным преимуществом использования этого метода является то, что вы можете легко включать данные из разнородных источников и различных уровней точности в математически согласованную модель. Это помогает сочетать экспертные знания с данными о переменных, которые не имеют данных.
