Redes Bayesianas: Introducción, Ejemplos y Aplicaciones Prácticas
Publicado: 2020-02-23Todos aquellos que alguna vez han trabajado con datos o estadísticas saben una cosa con certeza: correlación no necesariamente significa o implica causalidad. Ahora bien, si bien esto puede sonar bastante obvio, podría sorprenderlo saber que la mayoría de los errores en los datos ocurren debido a la confusión entre los dos términos. Esto se debe principalmente a que, si bien es conveniente definir la correlación, es casi imposible definir o cuantificar la causalidad.
De hecho, Judea Pearl, autora de Causality: Models, Reasoning, and Inference , afirma en el libro que los humanos enfocan sus esfuerzos matemáticos en inferencias probabilísticas y estadísticas, dejando las consideraciones causales “a merced de la intuición y el buen juicio”. Él dice que este es un factor importante que todavía estamos muy atrasados en términos de progreso científico.
Aquí es cuando las Redes Bayesianas nos lo ponen fácil. Nos ayudan a distinguir la correlación de la causalidad al permitirnos ver varias causas independientes a la vez. Todo esto se hace con precisión ya que los algoritmos de aprendizaje automático no funcionan en la subjetividad o la intuición; trabajan sobre datos.
Veamos un ejemplo para entender cómo operan las Redes Bayesianas.
Tabla de contenido
Ejemplo de Redes Bayesianas
Por el bien de este ejemplo, supongamos que el mundo está afectado por una enfermedad extremadamente rara pero fatal; digamos que hay una probabilidad de 1 en 1000 de que usted esté infectado por la enfermedad.
Ahora, para determinar si alguien padece la enfermedad, los médicos desarrollan una prueba. El problema es que solo tiene una precisión del 99%.

¿Cómo sabrá con certeza si tiene la enfermedad o no? ¿Tomar otra prueba afectará los resultados?
Veamos qué sucede cuando diriges…
Prueba 1
Como la enfermedad afecta solo a 1 de cada 1000, la probabilidad de que estés infectado es:
| Infectado | 0.001 |
| Gratis | 0.999 |
Enfermedad CPT (Tabla de probabilidad condicional)
Claramente, así como 1 de cada 1000 tiene posibilidades de padecer la enfermedad, 999 de cada 1000 están libres de ella.
Del mismo modo, crearemos una tabla para calcular la probabilidad de la prueba. Como se mencionó anteriormente, si la prueba es solo 99% precisa. Eso significa que solo hay un 99% de posibilidades de que el resultado sea verdadero. Similar es el caso de los resultados negativos.
| Presencia de virus | Infectado | Gratis |
| Prueba 1 (Positivo) | 0.99 | 0.01 |
| Prueba 1 (Negativo) | 0.01 | 0.99 |
Test1 CPT (Tabla de probabilidad condicional)
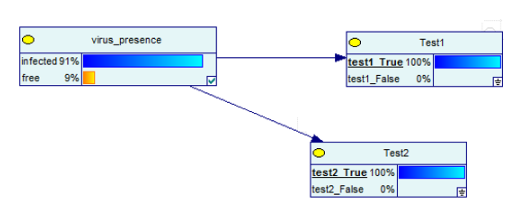
Ahora, hagamos un gráfico para ver cómo la presencia de la enfermedad se ve afectada por los resultados de la prueba.
Llenar estas celdas con los resultados de la prueba me dará el siguiente resultado.

Fuente de imagen
Como puedes ver, si la prueba da positivo, solo hay un 9% de posibilidades de que estés padeciendo la enfermedad.
Ahora, ¿cómo obtuvimos este número?
¡Teorema de Bayes!
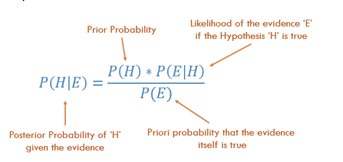
Fuente de imagen
En nuestro ejemplo,
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9 %
¿Qué nos dice esto?
Incluso cuando la prueba es positiva, debido a que la enfermedad es rara, solo hay un 9% de posibilidades de tener la enfermedad.
Entonces, ¿qué pasa cuando te haces otra prueba para estar seguro y también resulta positiva?
Leer: Ideas de proyectos de aprendizaje automático para principiantes
prueba 2
Nuevamente, la segunda prueba también solo tendrá una precisión del 99%.
| Presencia de virus | Infectado | Gratis |
| Prueba 2 (Positivo) | 0.99 | 0.01 |
| Prueba 2 (Negativo) | 0.01 | 0.99 |
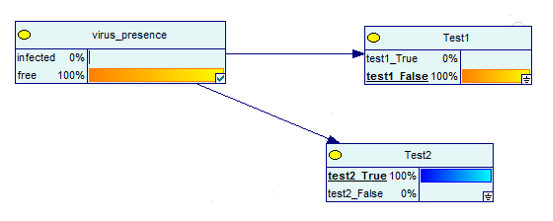
La Red Bayesiana ahora sería:
Fuente de imagen
¡Los resultados se han invertido!
Esto significa que si obtiene dos resultados positivos en dos pruebas, las probabilidades de ser infectado por el virus aumentan del 9% al 91%. Pero de nuevo, ¡no dice 100%!
Ahora, ¿qué sucede si obtiene un resultado positivo y otro negativo de la prueba?
Fuente de imagen
Como puede ver, hay un 100% de posibilidades de que no tenga la enfermedad en caso de que una de las dos pruebas sea negativa.
Prueba 3
Se vuelve aún mejor cuando realiza tres pruebas y todas resultan ser ciertas.

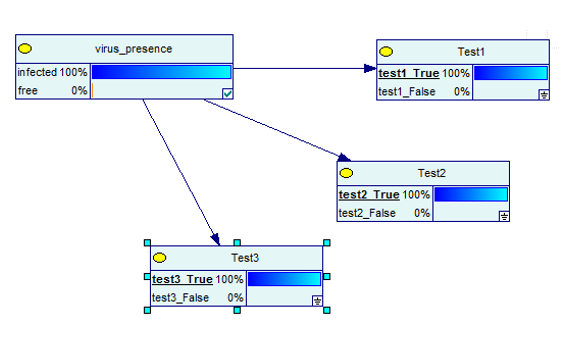
Fuente de imagen
Claramente, ahora, hay un 100% de posibilidades de que estés infectado.
Ahora veamos qué sucede cuando una de las pruebas es negativa pero las otras dos son positivas.
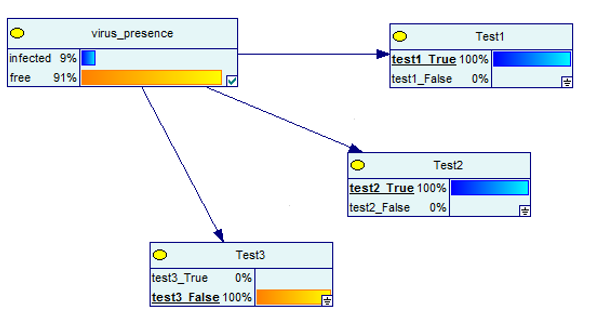
Fuente de imagen
Nuevamente, los resultados son 91% positivos para la presencia de un virus.
Modelado de datos y redes bayesianas
En el ejemplo anterior, se puede ver que las redes bayesianas juegan un papel importante cuando se trata de modelar datos para ofrecer resultados precisos.
De hecho, refinar la red al incluir más factores que puedan afectar el resultado también nos permite visualizar y simular diferentes escenarios usando Redes Bayesianas.
Las redes bayesianas también son una gran herramienta para cuantificar la injusticia en los datos y seleccionar técnicas para disminuir esta injusticia.
En tales casos, es mejor utilizar técnicas específicas de la ruta para identificar los factores sensibles que afectan los resultados finales.
Las 5 principales aplicaciones prácticas de las redes bayesianas
Las redes bayesianas se utilizan ampliamente en el campo de la ciencia de datos para obtener resultados precisos con datos inciertos.
Aplicaciones de Redes Bayesianas
1. Filtro de correo no deseado
Debe estar mintiendo si dice que nunca se ha preguntado cómo Gmail filtra los correos electrónicos no deseados (correos electrónicos no deseados y no solicitados). Utiliza el filtro de correo no deseado bayesiano, que es el filtro más sólido.
2. Código Turbo
Las redes bayesianas se utilizan para crear códigos turbo que son códigos de corrección de errores de reenvío de alto rendimiento. Estos se utilizan en redes móviles 3G y 4G.
3. Procesamiento de imágenes
Las redes bayesianas utilizan operaciones matemáticas para convertir imágenes a formato digital. También permite la mejora de la imagen.

4. Biomonitoreo
La cuantificación de la concentración de productos químicos no podría ser más fácil que con las redes bayesianas. En esto, la cantidad de sangre y tejido en humanos se mide usando indicadores.
5. Red de Regulación de Genes (GNR)
Un GNR contiene varios segmentos de ADN de una célula que interactúan con otros contenidos celulares a través de productos de expresión de proteínas y ARN. Las predicciones de su comportamiento se pueden analizar utilizando Redes Bayesianas.
Conclusión
En esta publicación de blog en línea, aprendió cómo las redes bayesianas nos ayudan a obtener resultados precisos a partir de los datos disponibles. Incluso la pequeña variación en los datos puede afectar significativamente el resultado final. Las redes bayesianas nos ayudan a analizar los datos utilizando la causalidad en lugar de solo la correlación.
Han demostrado ser revolucionarios en el campo de la ciencia de datos. Claramente, emprender una carrera en esta ciencia puede ayudarte a conseguir el trabajo de tus sueños. ¡Entonces, inscríbase en uno de nuestros cursos en ciencia de datos y aprenda de los expertos! También ofrecemos apoyo profesional gratuito de parte de asesores profesionales experimentados y de primer nivel. Descarga el folleto para obtener más información sobre el curso.
Si desea obtener más información sobre carreras en aprendizaje automático e inteligencia artificial, consulte IIT Madras y la certificación avanzada en aprendizaje automático y nube de upGrad.
¿Cuáles son los componentes de una red bayesiana?
Las Redes Bayesianas tienen su origen en el Teorema de Bayes, que lleva el nombre de Thomas Bayes, el famoso matemático británico. Este teorema es esencialmente una fórmula matemática utilizada para determinar la probabilidad condicional. Las redes bayesianas en el campo de la inteligencia artificial se derivan de las estadísticas bayesianas, que tienen el teorema de Bayes como su capa fundamental. Una red bayesiana consta de dos módulos: probabilidad condicional en el módulo cuantitativo y gráfico acíclico dirigido en su módulo cualitativo. En inteligencia artificial y aprendizaje automático, las redes bayesianas son herramientas que se utilizan para razonar y modelar basándose en creencias inciertas.
¿Cuánta probabilidad y estadística necesita saber para el aprendizaje automático?
Una parte considerable de la IA y sus diferentes subcampos se basan en la probabilidad y la estadística. Cuando se trata de aprendizaje automático, debe considerarlo más como un campo interdisciplinario, que emplea probabilidad, estadísticas y varios algoritmos. La estadística y la probabilidad son campos relacionados de las matemáticas que se utilizan para analizar la ocurrencia relativa de eventos. Esta combinación de estadísticas, probabilidad y algoritmos se usa en última instancia para crear aplicaciones inteligentes que aprenden de los datos y también ofrecen información valiosa. Por lo tanto, una comprensión básica de las estadísticas y la probabilidad es obligatoria si desea aprender el aprendizaje automático. Debe estar familiarizado con conceptos fundamentales como probabilidad empírica y teórica, probabilidad conjunta, probabilidad condicional, teorema de Bayes, estadística descriptiva, estadística descriptiva univariante y bivariante, correlación, etc.
¿Cuáles son las ventajas de usar Redes Bayesianas en IA?
Las redes bayesianas son una técnica muy popular para crear modelos para dominios complejos e inciertos. Con las redes bayesianas, puede desarrollar un marco matemáticamente lógico y sólido para paisajes inciertos como los ecosistemas y la gestión ambiental. La ventaja más significativa de usar esta técnica es que puede incorporar fácilmente datos de fuentes heterogéneas y niveles de precisión variables en un modelo matemáticamente coherente. Esto ayuda a combinar el conocimiento experto con datos sobre variables que no tienen ningún dato.
