Reti bayesiane: introduzione, esempi e applicazioni pratiche
Pubblicato: 2020-02-23Tutti coloro che hanno lavorato con dati o statistiche sanno per certo una cosa: la correlazione non significa necessariamente o implica causalità. Ora, anche se questo può sembrare abbastanza ovvio, potrebbe sconvolgerti nell'apprendere che la maggior parte degli errori nei dati si verificano a causa della confusione tra i due termini. Ciò è principalmente dovuto al fatto che, sebbene sia conveniente definire la correlazione, è quasi impossibile definire o quantificare la causalità.
In effetti, Judea Pearl, autrice di Causality: Models, Reasoning, and Inference , afferma nel libro che gli esseri umani concentrano i loro sforzi matematici su inferenze probabilistiche e statistiche, lasciando le considerazioni causali "alla mercé dell'intuizione e del buon giudizio". Dice che questo è un fattore importante che siamo ancora molto indietro in termini di progresso scientifico.
Questo è il momento in cui le reti bayesiane ci semplificano le cose. Ci aiutano a distinguere la correlazione dalla causalità consentendoci di vedere varie cause indipendenti contemporaneamente. Tutto questo viene fatto con precisione poiché gli algoritmi di apprendimento automatico non funzionano sulla soggettività o sull'intuizione; lavorano sui dati.
Vediamo un esempio per capire come funzionano le reti bayesiane.
Sommario
Esempio di reti bayesiane
Per il bene di questo esempio, supponiamo che il mondo sia colpito da una malattia estremamente rara ma fatale; diciamo che c'è una probabilità su 1000 di essere infettati dalla malattia.
Ora, per capire se qualcuno soffre della malattia, i medici sviluppano un test. Il problema è che è accurato solo al 99%.

Come saprai con certezza se hai la malattia o meno? Fare un altro test influenzerà i risultati?
Vediamo cosa succede quando conduci...
Prova 1
Poiché la malattia colpisce solo 1 su 1000, la probabilità che tu venga infettato è:
| Infetto | 0,001 |
| Libero | 0,999 |
Malattia CPT (tabella di probabilità condizionale)
Chiaramente, così come 1 su 1000 ha la possibilità di soffrire della malattia, 999 su 1000 ne sono esenti.
Allo stesso modo creeremo una tabella per calcolare la probabilità del test. Come accennato in precedenza, se il test è accurato solo al 99%. Ciò significa che c'è solo una probabilità del 99% che il risultato sia vero. Simile è il caso con risultati negativi.
| Presenza di virus | Infetto | Libero |
| Test 1 (positivo) | 0,99 | 0.01 |
| Test 1 (negativo) | 0.01 | 0,99 |
Test1 CPT (Tabella di probabilità condizionale)
Ora, tracciamo un grafico per vedere come la presenza della malattia è influenzata dai risultati del test.
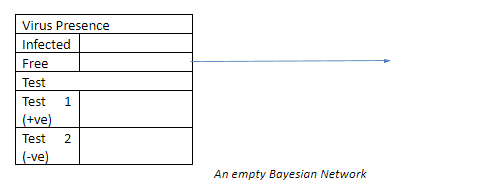
Riempire queste celle con i risultati del test mi darà il seguente risultato.

Fonte immagine
Come puoi vedere, se il test risulta positivo, c'è solo il 9% di probabilità che tu sia affetto dalla malattia.
Ora, come abbiamo ottenuto questo numero?
Teorema di Bayes!
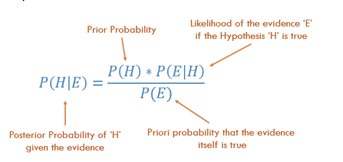
Fonte immagine
Nel nostro esempio,
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9%
Cosa ci dice questo?
Anche quando il test è positivo, poiché la malattia è rara, c'è solo il 9% di possibilità di contrarre la malattia.
Quindi, allora, cosa succede quando fai un altro test per essere sicuro e anche questo risulta essere positivo.
Leggi: Idee per progetti di apprendimento automatico per principianti
Prova 2
Anche in questo caso, anche il secondo test sarà accurato solo al 99%.
| Presenza di virus | Infetto | Libero |
| Test 2 (positivo) | 0,99 | 0.01 |
| Test 2 (negativo) | 0.01 | 0,99 |
La rete bayesiana ora sarebbe:
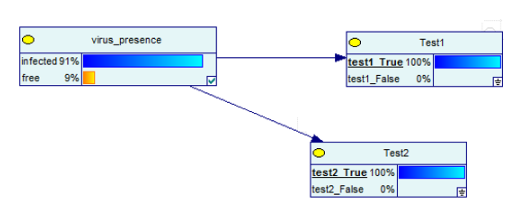
Fonte immagine
I risultati si sono invertiti!
Ciò significa che se si ottengono due risultati positivi su due test, le probabilità di essere infettati dal virus aumentano dal 9% al 91%. Ma ancora una volta, non dice 100%!
Ora, cosa succede se ottieni un risultato positivo e uno negativo dal test?
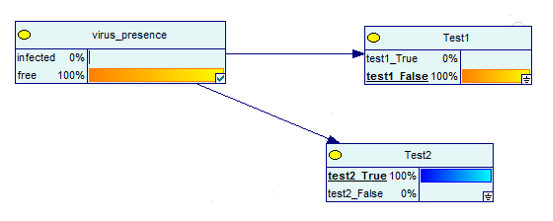
Fonte immagine
Come puoi vedere, c'è una probabilità del 100% che tu non abbia la malattia nel caso in cui uno dei due test sia negativo.
Prova 3
Diventa ancora meglio quando conduci tre test e tutti si rivelano veri.

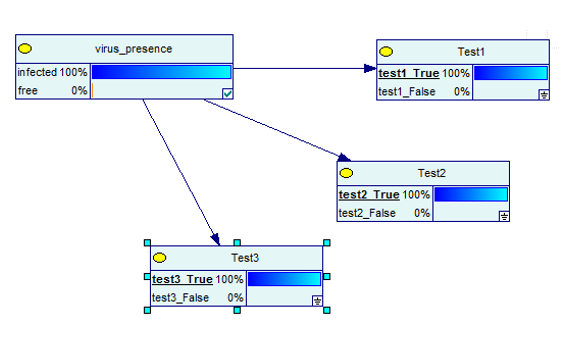
Fonte immagine
Chiaramente, ora, c'è una probabilità del 100% che tu sia infetto.
Ora vediamo cosa succede quando uno dei test è negativo ma gli altri due sono positivi.
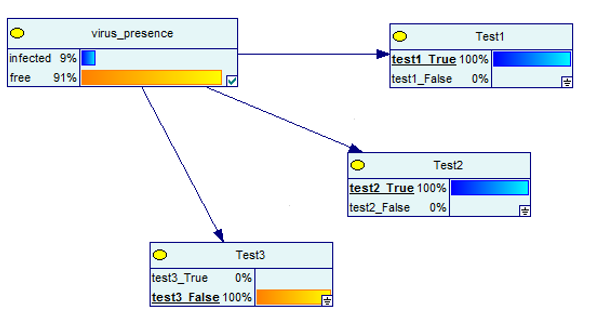
Fonte immagine
Anche in questo caso, i risultati sono positivi al 91% per la presenza di un virus.
Reti bayesiane e modellazione dei dati
Nell'esempio sopra, si può vedere che le reti bayesiane svolgono un ruolo significativo quando si tratta di modellare i dati per fornire risultati accurati.
In effetti, affinare la rete includendo più fattori che potrebbero influenzare il risultato ci consente anche di visualizzare e simulare diversi scenari utilizzando le reti bayesiane.
Le reti bayesiane sono anche un ottimo strumento per quantificare l'ingiustizia nei dati e curare le tecniche per ridurre questa iniquità.
In questi casi, è meglio utilizzare tecniche specifiche del percorso per identificare i fattori sensibili che influiscono sui risultati finali.
Le 5 migliori applicazioni pratiche delle reti bayesiane
Le reti bayesiane sono ampiamente utilizzate nel campo della scienza dei dati per ottenere risultati accurati con dati incerti.
Applicazioni delle reti bayesiane
1. Filtro antispam
Devi mentire se dici che non ti sei mai chiesto come Gmail filtra le e-mail di spam (e-mail indesiderate e non richieste. Utilizza il filtro antispam bayesiano, che è il filtro più robusto.
2. Codice Turbo
Le reti bayesiane vengono utilizzate per creare codici turbo che sono codici di correzione degli errori in avanti ad alte prestazioni. Questi sono utilizzati nelle reti mobili 3G e 4G.
3. Elaborazione delle immagini
Le reti bayesiane utilizzano operazioni matematiche per convertire le immagini in formato digitale. Consente inoltre il miglioramento dell'immagine.

4. Biomonitoraggio
Quantificare la concentrazione di sostanze chimiche non potrebbe essere più facile che con le reti bayesiane. In questo, la quantità di sangue e tessuto nell'uomo viene misurata utilizzando indicatori.
5. Rete di regolamentazione dei geni (GNR)
Un GNR contiene vari segmenti di DNA di una cellula che interagiscono con altri contenuti cellulari attraverso prodotti di espressione di proteine e RNA. Le previsioni del suo comportamento possono essere analizzate utilizzando le reti bayesiane.
Conclusione
In questo post sul blog online, hai appreso come le reti bayesiane ci aiutano a ottenere risultati accurati dai dati disponibili. Anche la minima variazione dei dati può influire in modo significativo sul risultato finale. Le reti bayesiane ci aiutano ad analizzare i dati usando la causalità invece della semplice correlazione.
Si sono rivelati rivoluzionari nel campo della scienza dei dati. Chiaramente, intraprendere una carriera in questa scienza può aiutarti a ottenere il lavoro dei tuoi sogni. Quindi, iscriviti a uno dei nostri corsi di scienza dei dati e impara dagli esperti! Offriamo inoltre supporto professionale gratuito da parte di consulenti professionali di prim'ordine ed esperti. Scarica la brochure per saperne di più sul corso.
Se vuoi saperne di più sulle carriere in Machine Learning e Intelligenza Artificiale, dai un'occhiata a IIT Madras e alla certificazione avanzata di upGrad in Machine Learning e Cloud.
Quali sono i componenti di una rete bayesiana?
Le reti bayesiane hanno la loro origine nel teorema di Bayes, che prende il nome da Thomas Bayes, il famoso matematico britannico. Questo teorema è essenzialmente una formula matematica utilizzata per determinare la probabilità condizionale. Le reti bayesiane nel campo dell'intelligenza artificiale derivano dalla statistica bayesiana, che ha il teorema di Bayes come livello fondamentale. Una rete bayesiana è composta da due moduli: probabilità condizionale nel modulo quantitativo e grafo aciclico diretto nel modulo qualitativo. Nell'intelligenza artificiale e nell'apprendimento automatico, le reti bayesiane sono strumenti utilizzati per il ragionamento e la modellazione sulla base di convinzioni incerte.
Quanta probabilità e statistiche devi sapere per l'apprendimento automatico?
Una parte considerevole dell'IA e dei suoi diversi sottocampi si basa su probabilità e statistiche. Quando si tratta di machine learning, è necessario considerarlo più come un campo interdisciplinare, che impiega probabilità, statistiche e vari algoritmi. La statistica e la probabilità sono campi correlati della matematica utilizzati per analizzare il verificarsi relativo degli eventi. Questa combinazione di statistiche, probabilità e algoritmi viene utilizzata in ultima analisi per creare applicazioni intelligenti che apprendono dai dati e offrono anche preziose informazioni. Quindi, una conoscenza di base di statistica e probabilità è obbligatoria se vuoi imparare l'apprendimento automatico. Dovresti avere familiarità con concetti fondamentali come probabilità empirica e teorica, probabilità congiunta, probabilità condizionale, teorema di Bayes, statistica descrittiva, statistica descrittiva univariata e bivariata, correlazione, ecc.
Quali sono i vantaggi dell'utilizzo delle reti bayesiane nell'IA?
Le reti bayesiane sono una tecnica estremamente popolare per la creazione di modelli per domini complessi e incerti. Utilizzando le reti bayesiane, puoi sviluppare un framework matematicamente logico e robusto per paesaggi incerti come gli ecosistemi e la gestione dell'ambiente. Il vantaggio più significativo dell'utilizzo di questa tecnica è che è possibile incorporare facilmente dati provenienti da fonti eterogenee e livelli di accuratezza variabili in un modello matematicamente coerente. Questo aiuta a combinare le conoscenze degli esperti con i dati sulle variabili che non hanno dati.
