Rețele bayesiene: introducere, exemple și aplicații practice
Publicat: 2020-02-23Toți cei care au lucrat vreodată cu date sau statistici știu un lucru sigur: corelația nu înseamnă sau implică neapărat cauzalitate. Acum, deși acest lucru poate părea destul de evident, s-ar putea să vă șocheze să aflați că majoritatea erorilor de date apar din cauza confuziei dintre cei doi termeni. Acest lucru se datorează în primul rând pentru că, deși este convenabil să definiți corelația, este aproape imposibil de definit sau cuantificat cauzalitatea.
De fapt, Judea Pearl, autorul cărții Causality: Models, Reasoning, and Inference , afirmă în carte că oamenii își concentrează eforturile matematice pe inferențe probabilistice și statistice, lăsând considerațiile cauzale „la mila intuiției și bunei judecati”. El spune că acesta este un factor major cu care suntem încă foarte în urmă în ceea ce privește progresul științific.
Acesta este momentul în care rețelele Bayesian ne ușurează. Ele ne ajută să distingem corelația de cauzalitate, permițându-ne să vedem simultan diverse cauze independente. Toate acestea sunt făcute cu acuratețe, deoarece algoritmii de învățare automată nu funcționează pe subiectivitate sau intuiție; ei lucrează pe date.
Să vedem un exemplu pentru a înțelege cum funcționează rețelele bayesiene.
Cuprins
Exemplu de rețele bayesiene
De dragul acestui exemplu, să presupunem că lumea este lovită de o boală extrem de rară, dar fatală; spuneți că există o șansă de 1 din 1000 să fiți infectat de boală.
Acum, pentru a-și da seama dacă cineva suferă de boală, medicii dezvoltă un test. Problema este că este doar 99% precisă.

Cum vei ști cu siguranță dacă ai sau nu boala? Un alt test va afecta rezultatele?
Să vedem ce se întâmplă când conduci...
Testul 1
Deoarece boala afectează doar 1 din 1000, probabilitatea de a fi infectat este:
| Infectat | 0,001 |
| Gratuit | 0,999 |
CPT de boală (Tabelul probabilității condiționate)
În mod clar, la fel cum 1 din 1000 are șanse de a suferi de boală, 999 din 1000 sunt liberi de aceasta.
În mod similar, vom crea un tabel pentru a calcula probabilitatea testului. După cum am menționat anterior, dacă testul are o precizie de numai 99%. Asta înseamnă că există doar 99% șanse ca rezultatul să fie adevărat. La fel este și cazul rezultatelor negative.
| Prezența virusului | Infectat | Gratuit |
| Testul 1 (pozitiv) | 0,99 | 0,01 |
| Testul 1 (negativ) | 0,01 | 0,99 |
Test1 CPT (Tabelul probabilității condiționate)
Acum, să trasăm un grafic pentru a vedea cum prezența bolii este afectată de rezultatele testului.
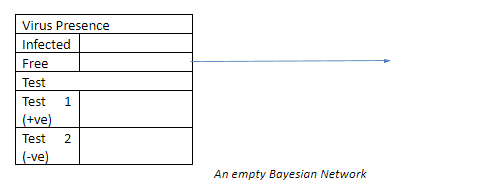
Umplerea acestor celule cu rezultatele testului îmi va da următorul rezultat.

Sursa imaginii
După cum puteți vedea, dacă testul iese pozitiv, există doar 9% șanse să suferiți de boală.
Acum, cum am obținut acest număr?
Teorema Bayes!
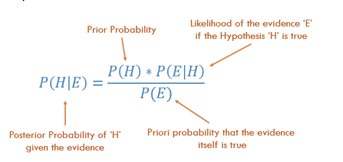
Sursa imaginii
În exemplul nostru,
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9%
Ce ne spune asta?
Chiar și atunci când testul este pozitiv, deoarece boala este rară, există doar 9% șanse de a avea boala.
Deci, atunci, ce se întâmplă când faci un alt test pentru a fi sigur și, de asemenea, se dovedește a fi pozitiv.
Citiți: Idei de proiecte de învățare automată pentru începători
Testul 2
Din nou, al doilea test va fi, de asemenea, o precizie de doar 99%.
| Prezența virusului | Infectat | Gratuit |
| Testul 2 (pozitiv) | 0,99 | 0,01 |
| Testul 2 (negativ) | 0,01 | 0,99 |
Rețeaua Bayesiană ar fi acum:
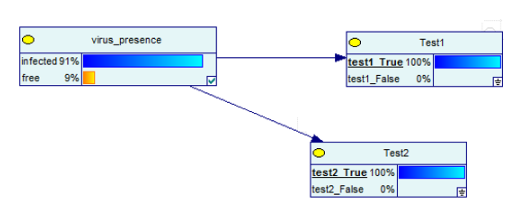
Sursa imaginii
Rezultatele s-au inversat!
Aceasta înseamnă că dacă obții două rezultate pozitive la două teste, șansele de a fi infectat cu virus cresc de la 9% la 91%. Dar din nou, nu spune 100%!
Acum, ce se întâmplă dacă obțineți un rezultat pozitiv și unul negativ de la test?
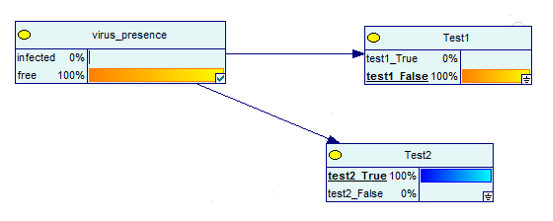
Sursa imaginii
După cum puteți vedea, există șanse de 100% să nu aveți boala în cazul în care unul dintre cele două teste este negativ.
Testul 3
Devine și mai bine atunci când efectuați trei teste și toate se dovedesc a fi adevărate.

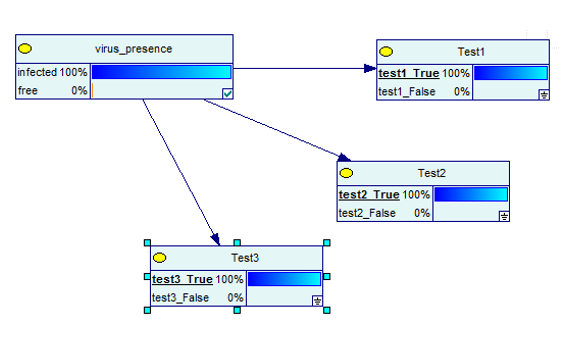
Sursa imaginii
În mod clar, acum, există o șansă de 100% să fii infectat.
Acum să vedem ce se întâmplă când unul dintre teste este negativ, dar celelalte două sunt pozitive.
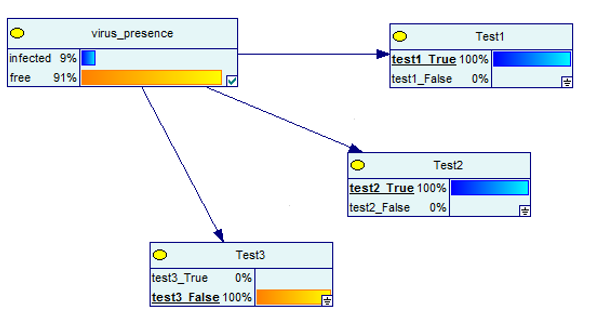
Sursa imaginii
Din nou, rezultatele sunt 91% pozitive pentru prezența unui virus.
Rețele bayesiene și modelare de date
În exemplul de mai sus, se poate observa că rețelele bayesiene joacă un rol semnificativ atunci când vine vorba de modelarea datelor pentru a oferi rezultate precise.
De fapt, rafinarea rețelei prin includerea mai multor factori care ar putea afecta rezultatul ne permite, de asemenea, să vizualizăm și să simulăm diferite scenarii folosind rețele Bayesian.
Rețelele Bayesian sunt, de asemenea, un instrument excelent pentru a cuantifica inechitabilitatea datelor și pentru a selecta tehnici pentru a reduce această inechitabilitate.
În astfel de cazuri, cel mai bine este să folosiți tehnici specifice căii pentru a identifica factorii sensibili care afectează rezultatele finale.
Top 5 aplicații practice ale rețelelor bayesiene
Rețelele Bayesiene sunt utilizate pe scară largă în domeniul științei datelor pentru a obține rezultate precise cu date incerte.
Aplicații ale rețelelor bayesiene
1. Filtru de spam
Trebuie să minți dacă spui că nu te-ai întrebat niciodată cum filtrează Gmail e-mailurile spam (e-mailurile nedorite și nesolicitate. Utilizează filtrul Bayesian de spam, care este cel mai robust filtru).
2. Cod Turbo
Rețelele Bayesian sunt folosite pentru a crea coduri turbo care sunt coduri de corectare a erorilor înainte de înaltă performanță. Acestea sunt utilizate în rețelele mobile 3G și 4G.
3. Procesarea imaginii
Rețelele Bayesiene folosesc operații matematice pentru a converti imaginile în format digital. De asemenea, permite îmbunătățirea imaginii.

4. Biomonitorizare
Cuantificarea concentrației de substanțe chimice nu ar putea deveni mai ușoară decât cu rețelele Bayesian. În aceasta, cantitatea de sânge și țesut la om este măsurată folosind indicatori.
5. Rețeaua de reglementare a genelor (GNR)
Un GNR conține diverse segmente de ADN ale unei celule care interacționează cu alte conținuturi celulare prin proteine și produse de exprimare a ARN. Predicțiile comportamentului său pot fi analizate folosind rețele bayesiene.
Concluzie
În această postare de blog online, ați aflat despre modul în care rețelele Bayesian ne ajută să obținem rezultate precise din datele disponibile. Chiar și micile variații ale datelor pot afecta semnificativ rezultatul final. Rețelele Bayesiene ne ajută să analizăm datele folosind cauzalitatea în loc de doar corelația.
S-au dovedit a fi revoluționari în domeniul științei datelor. În mod clar, începerea unei cariere în această știință vă poate ajuta să obțineți locul de muncă visat. Așadar, înscrieți-vă la unul dintre cursurile noastre de știința datelor și învățați de la experți! Oferim, de asemenea, suport gratuit în carieră de la consilieri de top și cu experiență. Descărcați broșura pentru a afla mai multe despre curs.
Dacă doriți să aflați mai multe despre carierele în învățarea automată și inteligența artificială, consultați IIT Madras și Certificarea avansată upGrad în învățare automată și cloud.
Care sunt componentele unei rețele bayesiene?
Rețelele Bayesiene își au originea în teorema Bayes, care poartă numele lui Thomas Bayes, celebrul matematician britanic. Această teoremă este în esență o formulă matematică folosită pentru a determina probabilitatea condiționată. Rețelele Bayesiene din domeniul inteligenței artificiale sunt derivate din Statistica Bayesiană, care are teorema Bayes ca strat de bază. O rețea bayesiană constă din două module – probabilitatea condiționată în modulul cantitativ și graficul aciclic direcționat în modulul său calitativ. În inteligența artificială și învățarea automată, rețelele bayesiene sunt instrumente utilizate pentru raționament și modelare bazate pe credințe incerte.
Câte probabilități și statistici trebuie să știți pentru învățarea automată?
O parte considerabilă a IA și diferitele sale subdomenii se bazează pe probabilități și statistici. Când vine vorba de învățarea automată, trebuie să îl considerați mai mult ca un domeniu interdisciplinar, care utilizează probabilități, statistici și diverși algoritmi. Statistica și probabilitatea sunt domenii conexe ale matematicii utilizate pentru a analiza apariția relativă a evenimentelor. Această combinație de statistici, probabilități și algoritmi este folosită în cele din urmă pentru a construi aplicații inteligente care învață din date și oferă, de asemenea, informații valoroase. Deci, o înțelegere de bază a statisticilor și probabilităților este obligatorie dacă doriți să învățați învățarea automată. Ar trebui să fiți familiarizați cu concepte fundamentale precum probabilitatea empirică și teoretică, probabilitatea comună, probabilitatea condiționată, teorema Bayes, statistica descriptivă, statistica descriptivă univariată și bivariată, corelația etc.
Care sunt avantajele utilizării rețelelor bayesiene în AI?
Rețelele Bayesiane sunt o tehnică extrem de populară pentru crearea de modele pentru domenii complexe și incerte. Folosind rețelele Bayesian, puteți dezvolta un cadru logic și robust din punct de vedere matematic pentru peisaje incerte precum ecosistemele și managementul mediului. Cel mai semnificativ avantaj al utilizării acestei tehnici este că puteți încorpora cu ușurință date din surse eterogene și niveluri de precizie diferite într-un model coerent din punct de vedere matematic. Acest lucru ajută la combinarea cunoștințelor de specialitate cu date despre variabile care nu au date.
