Sieci bayesowskie: wprowadzenie, przykłady i praktyczne zastosowania
Opublikowany: 2020-02-23Wszyscy, którzy kiedykolwiek pracowali z danymi lub statystykami, wiedzą na pewno jedno: korelacja niekoniecznie oznacza lub implikuje związek przyczynowy. Choć może się to wydawać dość oczywiste, może zaszokować, że większość błędów w danych powstaje z powodu pomylenia tych dwóch terminów. Dzieje się tak przede wszystkim dlatego, że chociaż wygodnie jest zdefiniować korelację, określenie lub ilościowe określenie związku przyczynowego jest prawie niemożliwe.
W rzeczywistości Judea Pearl, autorka Causality: Models, Reasoning, and Inference , stwierdza w książce, że ludzie koncentrują swoje matematyczne wysiłki na wnioskach probabilistycznych i statystycznych, pozostawiając przyczyny przyczynowe „na łasce intuicji i dobrego osądu”. Mówi, że jest to główny czynnik, za którym wciąż pozostajemy w tyle, jeśli chodzi o postęp naukowy.
Właśnie wtedy Bayesian Networks nam to ułatwia. Pomagają nam odróżnić korelację od przyczynowości, pozwalając nam zobaczyć jednocześnie różne niezależne przyczyny. Wszystko to jest zrobione dokładnie, ponieważ algorytmy uczenia maszynowego nie działają na subiektywności ani intuicji; pracują na danych.
Zobaczmy przykład, aby zrozumieć, jak działają sieci bayesowskie.
Spis treści
Przykład sieci bayesowskich
Ze względu na ten przykład przypuśćmy, że świat dotknięty jest niezwykle rzadką, lecz śmiertelną chorobą; powiedzmy, że istnieje 1 na 1000 szans, że jesteś zarażony chorobą.
Teraz, aby dowiedzieć się, czy ktoś cierpi na tę chorobę, lekarze opracowują test. Połów jest taki, że jest tylko 99% dokładny.

Skąd będziesz wiedzieć na pewno, czy masz chorobę, czy nie? Czy wykonanie kolejnego testu wpłynie na wyniki?
Zobaczmy, co się stanie, gdy przeprowadzisz…
Test 1
Ponieważ choroba dotyka tylko 1 na 1000, prawdopodobieństwo zarażenia wynosi:
| Zainfekowany | 0,001 |
| Bezpłatny | 0,999 |
Choroba CPT (tabela prawdopodobieństwa warunkowego)
Oczywiście tak jak 1 na 1000 ma szansę zachorować na tę chorobę, tak 999 osób na 1000 jest od niej wolnych.
Podobnie stworzymy tabelę do obliczenia prawdopodobieństwa testu. Jak wspomniano wcześniej, jeśli test jest dokładny tylko w 99%. Oznacza to, że istnieje tylko 99% szans, że wynik jest prawdziwy. Podobnie jest z wynikami negatywnymi.
| Obecność wirusa | Zainfekowany | Bezpłatny |
| Test 1 (pozytywny) | 0,99 | 0,01 |
| Test 1 (negatywny) | 0,01 | 0,99 |
Test1 CPT (tabela prawdopodobieństwa warunkowego)
Teraz narysujmy wykres, aby zobaczyć, jak na obecność choroby wpływają wyniki testu.
Wypełnienie tych komórek wynikami testu da mi następujący wynik.

Źródło obrazu
Jak widać, jeśli wynik testu będzie pozytywny, istnieje tylko 9% szans, że cierpisz na tę chorobę.
Jak otrzymaliśmy ten numer?
Twierdzenie Bayesa!
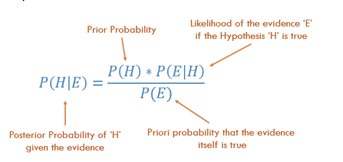
Źródło obrazu
W naszym przykładzie
P(H|E) = P(H) x P(E|H) / P(E)
- P(H|E) = P(H) x P(E|H) / {P(E|H) x P(H) + P(E|Hc) x P(Ec)}
- P(H|E) = (0,99 x 0,001) / (0,001 x 0,99 + 0,999 x 0,01) = 0,9 = 9%
Co nam to mówi?
Nawet jeśli wynik testu jest pozytywny, ponieważ choroba jest rzadka, prawdopodobieństwo zachorowania na tę chorobę wynosi tylko 9%.
Tak więc, co się dzieje, gdy wykonujesz kolejny test, aby mieć pewność, i on również okazuje się pozytywny.
Przeczytaj: Pomysły na projekty uczenia maszynowego dla początkujących
Test 2
Ponownie, drugi test będzie również dokładny tylko w 99%.
| Obecność wirusa | Zainfekowany | Bezpłatny |
| Test 2 (pozytywny) | 0,99 | 0,01 |
| Test 2 (negatywny) | 0,01 | 0,99 |
Sieć Bayesowska byłaby teraz:
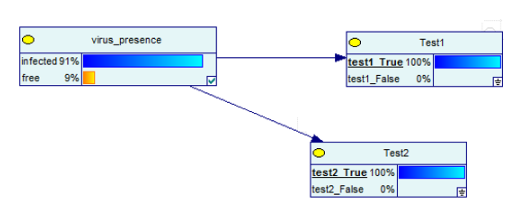
Źródło obrazu
Wyniki się odwróciły!
Oznacza to, że jeśli uzyskasz dwa pozytywne wyniki w dwóch testach, prawdopodobieństwo zarażenia wirusem wzrasta z 9% do 91%. Ale znowu, to nie mówi 100%!
A co, jeśli uzyskasz jeden pozytywny i jeden negatywny wynik testu?
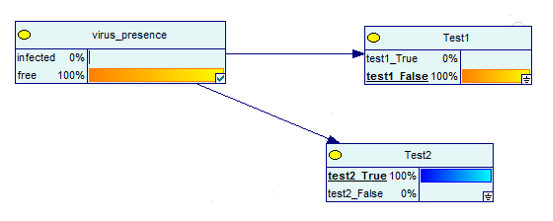
Źródło obrazu
Jak widać, istnieje 100% szansa, że nie masz choroby, jeśli jeden z dwóch testów jest negatywny.
Test 3
Jeszcze lepiej, gdy przeprowadzisz trzy testy i wszystkie okażą się prawdziwe.

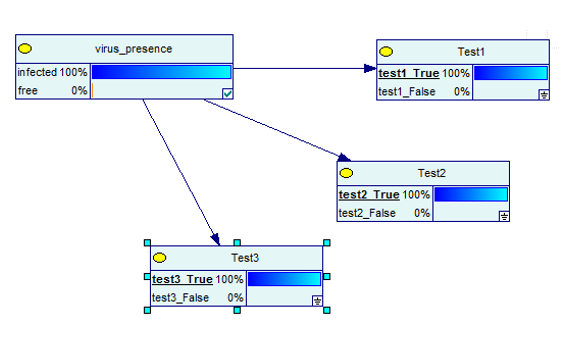
Źródło obrazu
Najwyraźniej teraz istnieje 100% szansa, że jesteś zarażony.
Zobaczmy teraz, co się dzieje, gdy jeden z testów jest negatywny, a pozostałe dwa są pozytywne.
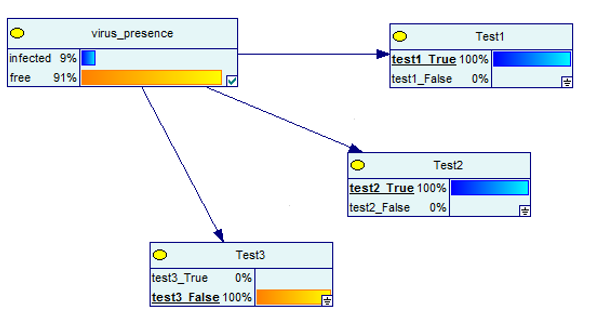
Źródło obrazu
Ponownie, wyniki są w 91% pozytywne na obecność wirusa.
Sieci bayesowskie i modelowanie danych
W powyższym przykładzie widać, że sieci bayesowskie odgrywają znaczącą rolę, jeśli chodzi o modelowanie danych w celu uzyskania dokładnych wyników.
W rzeczywistości udoskonalenie sieci poprzez uwzględnienie większej liczby czynników, które mogą wpłynąć na wynik, pozwala nam również na wizualizację i symulację różnych scenariuszy przy użyciu sieci bayesowskich.
Sieci bayesowskie są również doskonałym narzędziem do ilościowego określania nieuczciwości w danych i doboru technik zmniejszania tej nieuczciwości.
W takich przypadkach najlepiej jest użyć technik specyficznych dla ścieżki, aby zidentyfikować wrażliwe czynniki, które wpływają na wyniki końcowe.
5 najlepszych praktycznych zastosowań sieci bayesowskich
Sieci bayesowskie są szeroko stosowane w dziedzinie nauki o danych, aby uzyskać dokładne wyniki przy niepewnych danych.
Zastosowania sieci bayesowskich
1. Filtr spamu
Musisz kłamać, jeśli mówisz, że nigdy nie zastanawiałeś się, jak Gmail filtruje spam (niechciane i niechciane wiadomości e-mail. Używa filtru spamu Bayesa, który jest najbardziej niezawodnym filtrem).
2. Kod Turbo
Sieci bayesowskie są używane do tworzenia kodów turbo, które są wysokowydajnymi kodami korekcji błędów w przód. Są one używane w sieciach komórkowych 3G i 4G.
3. Przetwarzanie obrazu
Sieci bayesowskie wykorzystują operacje matematyczne do konwersji obrazów na format cyfrowy. Pozwala także na poprawę obrazu.

4. Biomonitoring
Ilościowe określenie stężenia chemikaliów nie mogło być prostsze niż w przypadku sieci Bayesowskich. W tym celu mierzy się ilość krwi i tkanki u ludzi za pomocą wskaźników.
5. Sieć regulacji genów (GNR)
GNR zawiera różne segmenty DNA komórki, które oddziałują z inną zawartością komórki poprzez produkty ekspresji białek i RNA. Przewidywania jego zachowania można analizować za pomocą sieci bayesowskich.
Wniosek
W tym internetowym poście na blogu dowiedziałeś się, w jaki sposób Bayesian Networks pomaga nam uzyskać dokładne wyniki na podstawie dostępnych danych. Nawet najmniejsza zmienność danych może znacząco wpłynąć na wynik końcowy. Sieci bayesowskie pomagają nam analizować dane za pomocą związku przyczynowego, a nie tylko korelacji.
Okazały się rewolucyjne w dziedzinie nauki o danych. Oczywiście podjęcie kariery w tej nauce może pomóc w zdobyciu wymarzonej pracy. Zapisz się więc na jeden z naszych kursów z zakresu nauki o danych i ucz się od ekspertów! Oferujemy również bezpłatne wsparcie zawodowe od najlepszych i doświadczonych doradców zawodowych. Pobierz broszurę, aby dowiedzieć się więcej o kursie.
Jeśli chcesz dowiedzieć się więcej o karierze w uczeniu maszynowym i sztucznej inteligencji, sprawdź IIT Madras i zaawansowaną certyfikację w zakresie uczenia maszynowego i chmury.
Jakie są składniki sieci bayesowskiej?
Sieci Bayesowskie wywodzą się z twierdzenia Bayesa, którego nazwa pochodzi od nazwiska słynnego brytyjskiego matematyka Thomasa Bayesa. Twierdzenie to jest zasadniczo formułą matematyczną używaną do określenia prawdopodobieństwa warunkowego. Sieci Bayesowskie w dziedzinie sztucznej inteligencji wywodzą się ze Statystyk Bayesowskich, których podstawową warstwą jest twierdzenie Bayesa. Sieć Bayesowska składa się z dwóch modułów – prawdopodobieństwa warunkowego w module ilościowym oraz skierowanego grafu acyklicznego w module jakościowym. W sztucznej inteligencji i uczeniu maszynowym sieci bayesowskie są narzędziami używanymi do wnioskowania i modelowania w oparciu o niepewne przekonania.
Ile prawdopodobieństwa i statystyk musisz znać, aby korzystać z uczenia maszynowego?
Znaczna część sztucznej inteligencji i jej różnych poddziedzin opiera się na prawdopodobieństwie i statystyce. Jeśli chodzi o uczenie maszynowe, należy traktować je bardziej jako dziedzinę interdyscyplinarną, która wykorzystuje prawdopodobieństwo, statystyki i różne algorytmy. Statystyka i prawdopodobieństwo to powiązane dziedziny matematyki używane do analizy względnego występowania zdarzeń. Ta kombinacja statystyk, prawdopodobieństwa i algorytmów jest ostatecznie wykorzystywana do tworzenia inteligentnych aplikacji, które uczą się na podstawie danych, a także oferują cenne informacje. Tak więc podstawowe zrozumienie statystyk i prawdopodobieństwa jest obowiązkowe, jeśli chcesz nauczyć się uczenia maszynowego. Powinieneś znać podstawowe pojęcia, takie jak prawdopodobieństwo empiryczne i teoretyczne, prawdopodobieństwo wspólne, prawdopodobieństwo warunkowe, twierdzenie Bayesa, statystyki opisowe, jednowymiarowe i dwuwymiarowe statystyki opisowe, korelacja itp.
Jakie są zalety korzystania z sieci Bayesian w AI?
Sieci bayesowskie to niezwykle popularna technika tworzenia modeli dla złożonych i niepewnych domen. Korzystając z sieci bayesowskich, można opracować matematycznie logiczną i solidną strukturę dla niepewnych krajobrazów, takich jak ekosystemy i zarządzanie środowiskiem. Najważniejszą zaletą stosowania tej techniki jest możliwość łatwego włączenia danych z heterogenicznych źródeł i różnych poziomów dokładności do matematycznie spójnego modelu. Pomaga to połączyć wiedzę ekspercką z danymi o zmiennych, które nie mają żadnych danych.
