기울기 하강 알고리즘: 방법론, 변형 및 모범 사례

최적화는 기계 학습의 필수적인 부분입니다. 거의 모든 기계 학습 알고리즘은 최적화 기능을 중요한 부분으로 가지고 있습니다. 단어에서 알 수 있듯이 기계 학습의 최적화는 문제 설명에 대한 최적의 솔루션을 찾는 것입니다.

이 기사에서는 가장 널리 사용되는 최적화 알고리즘 중 하나인 경사하강법에 대해 읽을 것입니다. 경사하강법 알고리즘 은 모든 기계 학습 알고리즘과 함께 사용할 수 있으며 이해하고 구현하기 쉽습니다. 그렇다면 경사하강법이란 정확히 무엇일까요? 이 기사를 마치면 경사하강법 알고리즘 과 이 알고리즘을 사용하여 모델의 매개변수를 업데이트하는 방법을 더 명확하게 이해하게 될 것입니다.

경사하강법

경사하강법 알고리즘에 대해 자세히 알아보기 전에 비용 함수가 무엇인지 알아야 합니다. 비용 함수는 주어진 데이터 세트에 대한 모델의 성능을 측정하는 데 사용되는 함수입니다. 예측값과 기대값의 차이를 찾아 오차 범위를 정량화합니다.

목표는 모델이 정확하도록 비용 함수를 줄이는 것입니다. 이 목표를 달성하려면 모델을 훈련하는 동안 필요한 매개변수를 찾아야 합니다. 기울기 하강법은 비용 함수를 줄이기 위해 함수의 계수를 찾는 데 사용되는 최적화 알고리즘 중 하나입니다. 비용 함수가 최소가 되는 지점을 전역 최소값이라고 합니다.

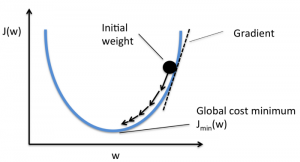
원천

Gradient Descent 알고리즘의 직관

과일이 들어 있는 것과 비슷한 큰 그릇이 있다고 가정합니다. 이 그릇은 비용 함수에 대한 플롯입니다. 그릇의 바닥은 비용 함수가 최소인 가장 좋은 계수입니다. 비용 함수를 계산하기 위한 계수로 다른 값이 사용됩니다. 이 단계는 최상의 계수를 찾을 때까지 반복됩니다.

공이 계곡을 굴러 내려가는 것처럼 경사하강법을 상상할 수 있습니다. 계곡은 여기에서 비용 함수에 대한 플롯입니다. 공이 계곡의 바닥에 도달하기를 원합니다. 여기서 계곡의 바닥은 최소 비용 함수를 나타냅니다. 공의 시작 위치에 따라 계곡의 많은 바닥에 놓일 수 있습니다. 그러나 이러한 바닥은 가장 낮은 점이 아닐 수 있으며 로컬 최소값으로 알려져 있습니다.

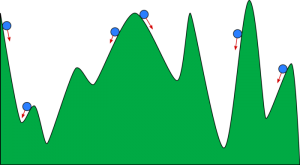
원천

읽기: 기계 학습 향상: 기능, 유형 및 특징

경사하강법 - 방법론

기울기 하강법의 계산은 함수에 대한 계수의 초기 값이 0 또는 작은 임의 값으로 설정되는 것으로 시작됩니다.

계수 = 0(또는 작은 값)

• 비용 함수는 이 계수 값을 함수에 넣어 계산됩니다.

비용 함수 = f(계수)

• 함수의 도함수가 함수의 기울기라는 것을 미적분의 개념에서 압니다. 기울기를 계산하면 계수 값을 이동하는 방향을 파악하는 데 도움이 됩니다. 방향은 다음 반복에서 더 낮은 비용(오류)을 얻는 방향이어야 합니다.

del = 미분(비용 함수)

• 경사에서 내리막 방향을 알고 나면 그에 따라 계수 값을 업데이트합니다. 학습률(알파)을 선택하여 각 반복에서 이러한 계수가 변경되는 정도를 제어할 수 있습니다. 이 학습률이 너무 높거나 낮지 않은지 확인해야 합니다.

계수 = 계수 – (알파 * 델)

• 이 과정은 비용 함수가 0이 되거나 0에 매우 가까워질 때까지 반복됩니다.

f(계수) = 0(또는 0에 가까움)

학습률의 선택이 중요합니다. 매우 높은 학습률을 선택하면 전역 최소값을 초과할 수 있습니다. 반대로 학습률이 매우 낮으면 전역 최소값에 도달하는 데 도움이 될 수 있지만 수렴이 매우 느리고 많은 반복이 필요합니다.

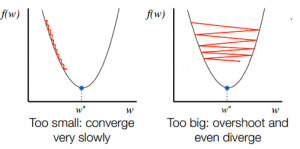
원천

경사 하강 알고리즘의 변형

배치 경사 하강법

배치 경사하강법은 경사하강법의 가장 많이 사용되는 변형 중 하나입니다 . 비용 함수는 모든 반복에 대해 전체 교육 데이터 세트에 대해 계산됩니다. 한 배치를 알고리즘의 한 반복이라고 하며 이 형식을 배치 경사하강법이라고 합니다.

확률적 경사하강법

어떤 경우에는 훈련 세트가 매우 클 수 있습니다. 이러한 경우 배치 경사 하강법은 훈련 세트의 각 인스턴스에 대해 한 번의 반복에 예측이 필요하기 때문에 계산하는 데 오랜 시간이 걸립니다. 데이터 세트가 거대한 이러한 조건에서 확률적 경사 하강법을 사용할 수 있습니다. 확률적 경사하강법에서 계수는 인스턴스 배치의 끝이 아니라 각 훈련 인스턴스에 대해 업데이트됩니다.

미니 배치 경사하강법

배치 경사하강법과 확률적 경사하강법 모두 장단점이 있습니다. 그러나 배치 경사 하강법과 확률적 경사 하강법을 혼합하여 사용하는 것이 유용할 수 있습니다. 미니 배치 경사 하강법에서는 전체 데이터 세트가 사용되지 않으며 한 번에 단일 인스턴스도 사용하지 않습니다. 훈련 사례 그룹을 고려합니다. 이 그룹의 예제 수가 전체 데이터 세트보다 적으며 이 그룹을 미니 배치라고 합니다.

경사하강법 모범 사례

• 비용 대 시간 매핑: 시간 에 대한 비용을 도표화하면 각 반복 후에 비용이 감소하는지 여부를 시각화하는 데 도움이 됩니다. 비용이 변경되지 않은 상태로 유지되는 경우 학습률을 업데이트해 보십시오.
• 학습률 : 학습률은 매우 낮으며 종종 0.01 또는 0.001로 선택됩니다. 어떤 값이 가장 적합한지 시도하고 확인해야 합니다.
• 입력 재조정: 경사하강법 알고리즘 은 모든 입력 변수가 [0, 1] 또는 [-1, 1]과 같은 동일한 범위로 재조정되는 경우 비용 함수를 더 빠르게 최소화합니다.
• 더 적은 패스: 일반적으로 확률적 경사하강법 알고리즘 은 최상의 계수를 찾기 위해 10번 이상의 패스가 필요하지 않습니다.

확인: 25가지 기계 학습 인터뷰 질문 및 답변

마무리

기계 학습 알고리즘을 최적화하는 데 있어 경사하강법의 역할을 알게 됩니다. 명심해야 할 한 가지 중요한 요소는 최적의 예측을 위해 경사하강법 알고리즘 에 적합한 학습률을 선택하는 것입니다.

upGrad는 기계 학습 및 AI 분야의 PG 디플로마와 기계 학습 및 AI 분야 의 석사 과정을 제공하여 경력을 쌓도록 안내합니다. 이 과정에서는 기계 학습의 필요성과 경사하강법 알고리즘 에서 신경망 에 이르는 다양한 개념을 다루는 이 영역에서 지식을 수집하기 위한 추가 단계를 설명합니다 .