Алгоритм градиентного спуска: методология, варианты и лучшие практики

Оптимизация является неотъемлемой частью машинного обучения. Практически все алгоритмы машинного обучения имеют функцию оптимизации в качестве ключевого сегмента. Как следует из самого слова, оптимизация в машинном обучении — это поиск оптимального решения поставленной задачи.

В этой статье вы прочтете об одном из наиболее широко используемых алгоритмов оптимизации — градиентном спуске. Алгоритм градиентного спуска можно использовать с любым алгоритмом машинного обучения, его легко понять и реализовать. Итак, что же такое градиентный спуск? К концу этой статьи у вас будет более четкое представление об алгоритме градиентного спуска и о том, как его можно использовать для обновления параметров модели.

Градиентный спуск

Прежде чем углубляться в алгоритм градиентного спуска, вы должны знать, что такое функция стоимости. Функция стоимости — это функция, используемая для измерения производительности вашей модели для данного набора данных. Он находит разницу между вашим прогнозируемым значением и ожидаемым значением, таким образом определяя погрешность.

Цель состоит в том, чтобы уменьшить функцию стоимости, чтобы модель была точной. Для достижения этой цели вам необходимо найти необходимые параметры во время обучения вашей модели. Градиентный спуск — это один из таких алгоритмов оптимизации, используемый для нахождения коэффициентов функции для уменьшения функции стоимости. Точка, в которой функция стоимости минимальна, называется глобальным минимумом.

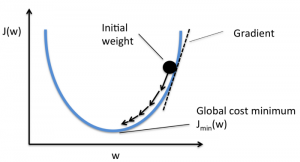
Источник

Интуиция, стоящая за алгоритмом градиентного спуска

Предположим, у вас есть большая миска, похожая на ту, в которой лежат ваши фрукты. Эта миска является графиком для функции стоимости. Дно чаши — это лучший коэффициент, при котором функция стоимости минимальна. Различные значения используются в качестве коэффициентов для расчета функции стоимости. Этот шаг повторяется до тех пор, пока не будут найдены лучшие коэффициенты.

Вы можете представить градиентный спуск как мяч, катящийся по долине. Долина — это график функции стоимости. Вы хотите, чтобы мяч достиг дна впадины, где дно впадины представляет функцию наименьших затрат. В зависимости от начального положения мяча он может лежать на многих днах долины. Однако эти впадины могут не быть самыми низкими точками и известны как локальные минимумы.

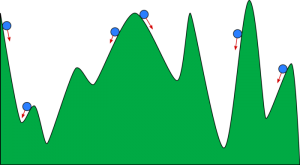
Источник

Читайте: Буст в машинном обучении: что такое, функции, типы и особенности

Алгоритм градиентного спуска - методология

Расчет градиентного спуска начинается с того, что начальные значения коэффициентов для функции задаются равными 0 или малым случайным значением.

коэффициент = 0 (или небольшое значение)

• Функция стоимости рассчитывается путем помещения этого значения коэффициента в функцию.

Функция стоимости = f (коэффициент)

• Мы знаем из концепции исчисления, что производная функции есть наклон функции. Вычисление наклона поможет вам определить направление перемещения значений коэффициента. Направление должно быть таким, чтобы вы получили меньшую стоимость (ошибку) в следующей итерации.

del = производная (функция стоимости)

• Зная направление спуска от склона, вы соответствующим образом обновляете значения коэффициентов. Можно выбрать скорость обучения (альфа), чтобы контролировать, насколько эти коэффициенты будут изменяться на каждой итерации. Вы должны убедиться, что эта скорость обучения не слишком высока и не слишком низка.

коэффициент = коэффициент – (альфа * дел)

• Этот процесс повторяется до тех пор, пока функция стоимости не станет равной 0 или очень близкой к 0.

f(коэффициент) = 0 (или близко к 0)

Выбор скорости обучения очень важен. Выбор очень высокой скорости обучения может превысить глобальные минимумы. Наоборот, очень низкая скорость обучения может помочь вам достичь глобальных минимумов, но сходимость будет очень медленной, требующей множества итераций.

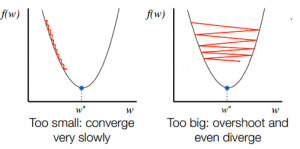
Источник

Варианты алгоритма градиентного спуска

Пакетный градиентный спуск

Пакетный градиентный спуск — один из наиболее часто используемых вариантов алгоритма градиентного спуска. Функция стоимости вычисляется по всему набору обучающих данных для каждой итерации. Одна партия называется одной итерацией алгоритма, и эта форма известна как пакетный градиентный спуск.

Стохастический градиентный спуск

В некоторых случаях обучающая выборка может быть очень большой. В этих случаях для вычисления пакетного градиентного спуска потребуется много времени, поскольку для одной итерации требуется прогноз для каждого экземпляра в обучающем наборе. Вы можете использовать стохастический градиентный спуск в этих условиях, когда набор данных огромен. При стохастическом градиентном спуске коэффициенты обновляются для каждого экземпляра обучения, а не в конце пакета экземпляров.

Мини-пакетный градиентный спуск

И пакетный градиентный спуск, и стохастический градиентный спуск имеют свои плюсы и минусы. Тем не менее, использование смеси пакетного градиентного спуска и стохастического градиентного спуска может быть полезным. В мини-пакетном градиентном спуске не используется ни весь набор данных, ни один экземпляр за раз. Вы принимаете во внимание группу обучающих примеров. Количество примеров в этой группе меньше, чем весь набор данных, и эта группа известна как мини-пакет.

Лучшие практики для алгоритма градиентного спуска

• Сопоставление стоимости со временем: построение графика зависимости стоимости от времени помогает визуализировать, уменьшается ли стоимость после каждой итерации. Если вы видите, что стоимость не изменилась, попробуйте обновить скорость обучения.
• Скорость обучения: Скорость обучения очень низкая и часто выбирается как 0,01 или 0,001. Вам нужно попробовать и посмотреть, какое значение лучше всего подходит для вас.
• Масштабирование входных данных: алгоритм градиентного спуска минимизирует функцию стоимости быстрее, если все входные переменные масштабируются до одного и того же диапазона, например [0, 1] или [-1, 1].
• Меньше проходов: обычно алгоритму стохастического градиентного спуска не требуется более 10 проходов, чтобы найти лучшие коэффициенты.

Проверьте: 25 вопросов и ответов на собеседовании по машинному обучению

Подведение итогов

Вы узнаете роль градиентного спуска в оптимизации алгоритма машинного обучения. Одним из важных факторов, о котором следует помнить, является выбор правильной скорости обучения для вашего алгоритма градиентного спуска для оптимального прогнозирования.

upGrad предоставляет диплом PG в области машинного обучения и искусственного интеллекта и степень магистра наук в области машинного обучения и искусственного интеллекта , которые могут помочь вам построить карьеру. Эти курсы объяснят необходимость машинного обучения и дальнейшие шаги по сбору знаний в этой области, охватывающие различные концепции, от алгоритмов градиентного спуска до нейронных сетей.