Algorithme de descente de gradient : méthodologie, variantes et meilleures pratiques

L'optimisation fait partie intégrante de l'apprentissage automatique. Presque tous les algorithmes d'apprentissage automatique ont une fonction d'optimisation en tant que segment crucial. Comme le mot l'indique, l'optimisation de l'apprentissage automatique consiste à trouver la solution optimale à un énoncé de problème.

Dans cet article, vous découvrirez l'un des algorithmes d'optimisation les plus utilisés, la descente de gradient. L' algorithme de descente de gradient peut être utilisé avec n'importe quel algorithme d'apprentissage automatique et est facile à comprendre et à mettre en œuvre. Alors, qu'est-ce que la descente de gradient exactement ? À la fin de cet article, vous aurez une meilleure compréhension de l' algorithme de descente de gradient et de la façon dont il peut être utilisé pour mettre à jour les paramètres du modèle.

Descente graduelle

Avant d'approfondir l' algorithme de descente de gradient, vous devez savoir ce qu'est la fonction de coût. La fonction de coût est une fonction utilisée pour mesurer les performances de votre modèle pour un jeu de données donné. Il trouve la différence entre votre valeur prédite et la valeur attendue, quantifiant ainsi la marge d'erreur.

L'objectif est de réduire la fonction de coût afin que le modèle soit précis. Pour atteindre cet objectif, vous devez trouver les paramètres requis lors de la formation de votre modèle. La descente de gradient est un tel algorithme d'optimisation utilisé pour trouver les coefficients d'une fonction afin de réduire la fonction de coût. Le point auquel la fonction de coût est minimale est appelé minima global.

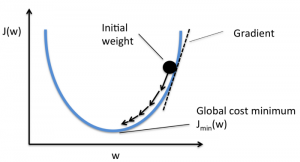
La source

L'intuition derrière l'algorithme Gradient Descent

Supposons que vous ayez un grand bol semblable à quelque chose dans lequel vous avez vos fruits. Ce bol est le tracé de la fonction de coût. Le fond du bol est le meilleur coefficient pour lequel la fonction de coût est minimale. Différentes valeurs sont utilisées comme coefficients pour calculer la fonction de coût. Cette étape est répétée jusqu'à ce que les meilleurs coefficients soient trouvés.

Vous pouvez imaginer une descente en gradient comme une boule roulant dans une vallée. La vallée est le tracé de la fonction de coût ici. Vous voulez que la balle atteigne le fond de la vallée, où le fond de la vallée représente la fonction de moindre coût. Selon la position de départ de la balle, celle-ci peut reposer sur de nombreux fonds de vallée. Cependant, ces fonds peuvent ne pas être les points les plus bas et sont appelés minima locaux.

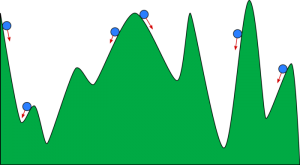
La source

Lis : Stimuler l'apprentissage automatique : qu'est-ce que c'est, les fonctions, les types et les fonctionnalités

Algorithme de descente de gradient - Méthodologie

Le calcul de la descente de gradient commence avec les valeurs initiales des coefficients pour la fonction étant fixées à 0 ou à une petite valeur aléatoire.

coefficient = 0 (ou une petite valeur)

• La fonction de coût est calculée en mettant cette valeur du coefficient dans la fonction.

Fonction de coût = f(coefficient)

• Nous savons du concept de calcul que la dérivée d'une fonction est la pente de la fonction. Le calcul de la pente vous aidera à déterminer la direction dans laquelle déplacer les valeurs de coefficient. La direction doit être telle que vous obtenez un coût (erreur) inférieur à la prochaine itération.

del = dérivée (fonction de coût)

• Après avoir connu la direction de descente à partir de la pente, vous mettez à jour les valeurs de coefficient en conséquence. Un taux d'apprentissage (alpha) peut être sélectionné pour contrôler la variation de ces coefficients à chaque itération. Vous devez vous assurer que ce taux d'apprentissage n'est ni trop élevé ni trop faible.

coefficient = coefficient – ​​(alpha * del)

• Ce processus est répété jusqu'à ce que la fonction de coût devienne 0 ou très proche de 0.

f(coefficient) = 0 (ou proche de 0)

Le choix du rythme d'apprentissage est important. La sélection d'un taux d'apprentissage très élevé peut dépasser les minima globaux. Au contraire, un taux d'apprentissage très faible peut vous aider à atteindre les minima globaux, mais la convergence est très lente, prenant de nombreuses itérations.

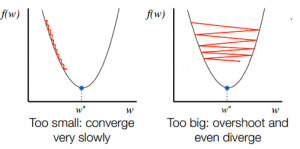
La source

Variantes de l'algorithme de descente de gradient

Descente de dégradé par lots

La descente de gradient par lots est l'une des variantes les plus utilisées de l' algorithme de descente de gradient. La fonction de coût est calculée sur l'ensemble de données d'apprentissage pour chaque itération. Un lot est appelé une itération de l'algorithme, et cette forme est connue sous le nom de descente de gradient de lot.

Descente de gradient stochastique

Dans certains cas, l'ensemble d'apprentissage peut être très volumineux. Dans ces cas, la descente de gradient par lots prendra beaucoup de temps à calculer car une itération nécessite une prédiction pour chaque instance de l'ensemble d'apprentissage. Vous pouvez utiliser la descente de gradient stochastique dans ces conditions où l'ensemble de données est énorme. En descente de gradient stochastique, les coefficients sont mis à jour pour chaque instance d'apprentissage et non à la fin du lot d'instances.

Descente de dégradé en mini lot

La descente de gradient par lots et la descente de gradient stochastique ont leurs avantages et leurs inconvénients. Cependant, l'utilisation d'un mélange de descente de gradient par lots et de descente de gradient stochastique peut être utile. Dans la descente de gradient en mini-lot, ni l'ensemble de données complet n'est utilisé ni une seule instance à la fois. Vous prenez en considération un groupe d'exemples de formation. Le nombre d'exemples dans ce groupe est inférieur à l'ensemble de données complet, et ce groupe est connu sous le nom de mini-lot.

Meilleures pratiques pour l'algorithme de descente de gradient

• Cartographier le coût en fonction du temps : tracer le coût en fonction du temps vous aide à visualiser si le coût diminue ou non après chaque itération. Si vous constatez que le coût reste inchangé, essayez de mettre à jour le taux d'apprentissage.
• Taux d'apprentissage : le taux d'apprentissage est très faible et est souvent sélectionné à 0,01 ou 0,001. Vous devez essayer de voir quelle valeur vous convient le mieux.
• Remettre à l'échelle les entrées : l' algorithme de descente de gradient minimisera la fonction de coût plus rapidement si toutes les variables d'entrée sont remises à l'échelle dans la même plage, comme [0, 1] ou [-1, 1].
• Moins de passes : Habituellement, l' algorithme de descente de gradient stochastique n'a pas besoin de plus de 10 passes pour trouver les meilleurs coefficients.

Départ: 25 questions et réponses d'entrevue sur l'apprentissage automatique

Emballer

Vous apprenez à connaître le rôle de la descente de gradient dans l'optimisation d'un algorithme d'apprentissage automatique. Un facteur important à garder à l'esprit est de choisir le bon taux d'apprentissage pour votre algorithme de descente de gradient pour une prédiction optimale.

upGrad fournit un diplôme PG en apprentissage automatique et IA et une maîtrise ès sciences en apprentissage automatique et IA qui peuvent vous guider vers la construction d'une carrière. Ces cours expliqueront la nécessité de l'apprentissage automatique et d'autres étapes pour rassembler des connaissances dans ce domaine couvrant des concepts variés allant des algorithmes de descente de gradient aux réseaux de neurones.