梯度下降算法：方法、变体和最佳实践

优化是机器学习的一个组成部分。 几乎所有机器学习算法都将优化功能作为关键部分。 正如这个词所暗示的，机器学习中的优化是找到问题陈述的最佳解决方案。

在本文中，您将了解使用最广泛的优化算法之一，梯度下降。 梯度下降算法可以与任何机器学习算法一起使用，并且易于理解和实现。 那么，梯度下降究竟是什么？ 在本文结束时，您将对梯度下降算法以及如何使用它来更新模型的参数有一个更清晰的了解。

梯度下降

在深入了解梯度下降算法之前，您应该知道什么是成本函数。 成本函数是用于衡量给定数据集的模型性能的函数。 它找到您的预测值和预期值之间的差异，从而量化误差范围。

目标是降低成本函数，使模型准确。 为了实现这一目标，您需要在模型的训练过程中找到所需的参数。 梯度下降是一种这样的优化算法，用于找到函数的系数以降低成本函数。 成本函数最小的点称为全局最小值。

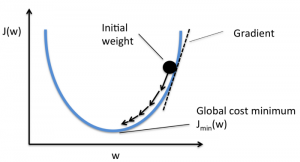
资源

梯度下降算法背后的直觉

假设你有一个大碗，类似于装水果的东西。这个碗是成本函数的图。 碗底是成本函数最小的最佳系数。 使用不同的值作为系数来计算成本函数。 重复此步骤，直到找到最佳系数。

你可以把梯度下降想象成一个滚下山谷的球。 谷是这里成本函数的图。 您希望球到达谷底，谷底代表最小的成本函数。 根据球的起始位置，它可能停留在山谷的许多底部。 然而，这些底部可能不是最低点，被称为局部最小值。

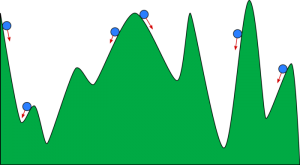
资源

阅读：促进机器学习：什么是、功能、类型和特征

梯度下降算法 - 方法论

梯度下降的计算从函数系数的初始值被设置为 0 或一个小的随机值开始。

系数 = 0（或小值）

• 成本函数是通过将该系数的值放入函数中来计算的。

成本函数 = f(系数)

• 我们从微积分的概念中知道，函数的导数是函数的斜率。 计算斜率将帮助您确定移动系数值的方向。 方向应该使您在下一次迭代中获得较低的成本（错误）。

del = 导数（成本函数）

• 在知道斜坡的下坡方向后，您相应地更新系数值。 可以选择学习率 (alpha) 来控制这些系数在每次迭代中的变化程度。 你需要确保这个学习率既不太高也不太低。

系数 = 系数 - (alpha * del)

• 重复此过程，直到成本函数变为 0 或非常接近 0。

f(系数) = 0 (或接近 0)

学习率的选择很重要。 选择一个非常高的学习率可能会超过全局最小值。 相反，非常低的学习率可以帮助你达到全局最小值，但收敛速度非常慢，需要多次迭代。

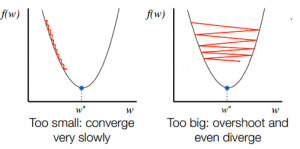
资源

梯度下降算法的变体

批量梯度下降

批量梯度下降是梯度下降算法最常用的变体之一。 成本函数是在每次迭代的整个训练数据集上计算的。 一批称为算法的一次迭代，这种形式称为批梯度下降。

随机梯度下降

在某些情况下，训练集可能非常大。 在这些情况下，批量梯度下降将需要很长时间来计算，因为一次迭代需要对训练集中的每个实例进行预测。 在数据集很大的情况下，您可以使用随机梯度下降。 在随机梯度下降中，系数会针对每个训练实例更新，而不是在实例批次结束时更新。

小批量梯度下降

批量梯度下降和随机梯度下降都有其优点和缺点。 然而，使用批量梯度下降和随机梯度下降的混合是有用的。 在小批量梯度下降中，既不会使用整个数据集，也不会一次使用单个实例。 您考虑了一组训练示例。 该组中的示例数量少于整个数据集，该组称为小批量。

梯度下降算法的最佳实践

• 绘制成本与时间的关系图：绘制相对于时间的成本有助于您可视化每次迭代后成本是否下降。 如果您看到成本保持不变，请尝试更新学习率。
• 学习率：学习率很低，常选为0.01或0.001。 您需要尝试看看哪种值最适合您。
• 重新缩放输入：如果将所有输入变量重新缩放到相同的范围，例如 [0, 1] 或 [-1, 1]，梯度下降算法将更快地最小化成本函数。
• 更少的通过次数：通常，随机梯度下降算法不需要超过 10 次通过即可找到最佳系数。

查看： 25 个机器学习面试问题和答案

包起来

您将了解梯度下降在优化机器学习算法中的作用。 要记住的一个重要因素是为您的梯度下降算法选择正确的学习率以获得最佳预测。

upGrad 提供机器学习和人工智能的PG 文凭和机器学习和人工智能的理学硕士，可以指导您建立职业生涯。 这些课程将解释机器学习的必要性以及收集该领域知识的进一步步骤，涵盖从梯度下降算法到神经网络的各种概念。