Gradientenabstiegsalgorithmus: Methodik, Varianten und Best Practices

Die Optimierung ist ein wesentlicher Bestandteil des maschinellen Lernens. Fast alle Machine-Learning-Algorithmen haben als entscheidendes Segment eine Optimierungsfunktion. Wie das Wort schon sagt, besteht die Optimierung beim maschinellen Lernen darin, die optimale Lösung für eine Problemstellung zu finden.

In diesem Artikel lesen Sie etwas über einen der am häufigsten verwendeten Optimierungsalgorithmen, den Gradientenabstieg. Der Gradientenabstiegsalgorithmus kann mit jedem maschinellen Lernalgorithmus verwendet werden und ist einfach zu verstehen und zu implementieren. Also, was genau ist Gradientenabstieg? Am Ende dieses Artikels haben Sie ein klareres Verständnis des Gradientenabstiegsalgorithmus und wie er verwendet werden kann, um die Parameter des Modells zu aktualisieren.

Gradientenabstieg

Bevor Sie sich eingehend mit dem Gradientenabstiegsalgorithmus befassen, sollten Sie wissen, was eine Kostenfunktion ist. Die Kostenfunktion ist eine Funktion, mit der die Leistung Ihres Modells für einen bestimmten Datensatz gemessen wird. Es findet die Differenz zwischen Ihrem vorhergesagten Wert und dem erwarteten Wert und quantifiziert so die Fehlerspanne.

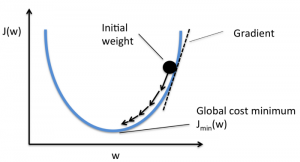
Das Ziel besteht darin, die Kostenfunktion so zu reduzieren, dass das Modell genau ist. Um dieses Ziel zu erreichen, müssen Sie die erforderlichen Parameter während des Trainings Ihres Modells finden. Der Gradientenabstieg ist ein solcher Optimierungsalgorithmus, der verwendet wird, um die Koeffizienten einer Funktion zu finden, um die Kostenfunktion zu reduzieren. Der Punkt, an dem die Kostenfunktion minimal ist, wird als globale Minima bezeichnet.

Quelle

Die Intuition hinter dem Gradient Descent-Algorithmus

Angenommen, Sie haben eine große Schale, ähnlich wie etwas, in dem Sie Ihr Obst aufbewahren. Diese Schale ist das Diagramm für die Kostenfunktion. Der Boden der Schüssel ist der beste Koeffizient, für den die Kostenfunktion minimal ist. Als Koeffizienten zur Berechnung der Kostenfunktion werden unterschiedliche Werte verwendet. Dieser Schritt wird wiederholt, bis die besten Koeffizienten gefunden sind.

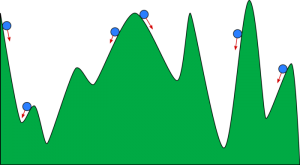
Sie können sich einen Gradientenabstieg wie einen Ball vorstellen, der ein Tal hinunterrollt. Das Tal ist hier das Diagramm für die Kostenfunktion. Sie möchten, dass der Ball den Boden des Tals erreicht, wo der Boden des Tals die Funktion mit den geringsten Kosten darstellt. Je nach Startposition des Balles kann dieser auf vielen Talsohlen aufliegen. Diese Böden sind jedoch möglicherweise nicht die niedrigsten Punkte und werden als lokale Minima bezeichnet.

Quelle

Lesen Sie: Steigerung des maschinellen Lernens: Was ist, Funktionen, Typen und Merkmale

Gradientenabstiegsalgorithmus - Methodik

Die Berechnung des Gradientenabstiegs beginnt damit, dass die Anfangswerte der Koeffizienten für die Funktion auf 0 oder einen kleinen Zufallswert gesetzt werden.

Koeffizient = 0 (oder ein kleiner Wert)

• Die Kostenfunktion wird berechnet, indem dieser Wert des Koeffizienten in die Funktion eingesetzt wird.

Kostenfunktion = f(Koeffizient)

• Wir wissen aus dem Konzept der Analysis, dass die Ableitung einer Funktion die Steigung der Funktion ist. Die Berechnung der Steigung hilft Ihnen, die Richtung herauszufinden, in der die Koeffizientenwerte verschoben werden müssen. Die Richtung sollte so sein, dass Sie in der nächsten Iteration geringere Kosten (Fehler) erhalten.

del = Ableitung (Kostenfunktion)

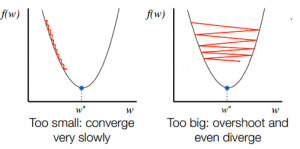
• Nachdem Sie die Richtung des Gefälles von der Steigung kennen, aktualisieren Sie die Koeffizientenwerte entsprechend. Eine Lernrate (Alpha) kann ausgewählt werden, um zu steuern, wie stark sich diese Koeffizienten bei jeder Iteration ändern. Sie müssen darauf achten, dass diese Lernrate weder zu hoch noch zu niedrig ist.

Koeffizient = Koeffizient – ​​(alpha * del)

• Dieser Vorgang wird wiederholt, bis die Kostenfunktion 0 wird oder sehr nahe bei 0 liegt.

f(Koeffizient) = 0 (oder nahe 0)

Wichtig ist die Wahl der Lernrate. Die Wahl einer sehr hohen Lernrate kann über die globalen Minima hinausschießen. Im Gegenteil, eine sehr niedrige Lernrate kann Ihnen helfen, die globalen Minima zu erreichen, aber die Konvergenz ist sehr langsam und erfordert viele Iterationen.

Quelle

Varianten des Gradientenabstiegsalgorithmus

Batch-Gradientenabstieg

Batch-Gradientenabstieg ist eine der am häufigsten verwendeten Varianten des Gradientenabstiegsalgorithmus. Die Kostenfunktion wird für jede Iteration über den gesamten Trainingsdatensatz berechnet. Ein Batch wird als eine Iteration des Algorithmus bezeichnet, und diese Form ist als Batch-Gradientenabstieg bekannt.

Stochastischer Gradientenabstieg

In einigen Fällen kann der Trainingssatz sehr groß sein. In diesen Fällen dauert die Berechnung des Batch-Gradientenabstiegs lange, da eine Iteration eine Vorhersage für jede Instanz im Trainingssatz benötigt. Unter diesen Bedingungen, bei denen der Datensatz riesig ist, können Sie den stochastischen Gradientenabstieg verwenden. Beim stochastischen Gradientenabstieg werden die Koeffizienten für jede Trainingsinstanz aktualisiert und nicht am Ende des Stapels von Instanzen.

Mini-Batch-Gradientenabstieg

Sowohl Batch-Gradientenabstieg als auch stochastischer Gradientenabstieg haben ihre Vor- und Nachteile. Es kann jedoch nützlich sein, eine Mischung aus Batch-Gradientenabstieg und stochastischem Gradientenabstieg zu verwenden. Beim Mini-Batch-Gradientenabstieg wird weder der gesamte Datensatz verwendet, noch verwenden Sie jeweils eine einzelne Instanz. Sie berücksichtigen eine Gruppe von Trainingsbeispielen. Die Anzahl der Beispiele in dieser Gruppe ist geringer als der gesamte Datensatz, und diese Gruppe wird als Minibatch bezeichnet.

Best Practices für den Gradientenabstiegsalgorithmus

• Kartierung der Kosten im Verhältnis zur Zeit: Durch die grafische Darstellung der Kosten im Verhältnis zur Zeit können Sie visualisieren, ob die Kosten nach jeder Iteration sinken oder nicht. Wenn Sie sehen, dass die Kosten unverändert bleiben, versuchen Sie, die Lernrate zu aktualisieren.
• Lernrate : Die Lernrate ist sehr gering und wird oft mit 0,01 oder 0,001 gewählt. Sie müssen ausprobieren, welcher Wert für Sie am besten geeignet ist.
• Eingaben neu skalieren: Der Gradientenabstiegsalgorithmus minimiert die Kostenfunktion schneller, wenn alle Eingabevariablen auf denselben Bereich neu skaliert werden, z. B. [0, 1] oder [-1, 1].
• Weniger Durchgänge: Normalerweise benötigt der stochastische Gradientenabstiegsalgorithmus nicht mehr als 10 Durchgänge, um die besten Koeffizienten zu finden.

Sehen Sie sich an: 25 Fragen und Antworten zu Interviews mit maschinellem Lernen

Einpacken

Sie lernen die Rolle des Gradientenabstiegs bei der Optimierung eines maschinellen Lernalgorithmus kennen. Ein wichtiger Faktor, den Sie im Auge behalten sollten, ist die Auswahl der richtigen Lernrate für Ihren Gradientenabstiegsalgorithmus für eine optimale Vorhersage.

upGrad bietet ein PG-Diplom in maschinellem Lernen und KI und einen Master of Science in maschinellem Lernen und KI , das Sie beim Aufbau einer Karriere unterstützen kann. Diese Kurse erklären die Notwendigkeit des maschinellen Lernens und weitere Schritte zum Sammeln von Wissen in diesem Bereich, die verschiedene Konzepte abdecken, die von Gradientenabstiegsalgorithmen bis hin zu neuronalen Netzwerken reichen.