Algoritmul de coborâre a gradientului: metodologie, variante și bune practici

Optimizarea este o parte integrantă a învățării automate. Aproape toți algoritmii de învățare automată au o funcție de optimizare ca segment crucial. După cum sugerează cuvântul, optimizarea în învățarea automată înseamnă găsirea soluției optime pentru o declarație de problemă.

În acest articol, veți citi despre unul dintre cei mai folosiți algoritmi de optimizare, coborârea gradientului. Algoritmul de coborâre a gradientului poate fi utilizat cu orice algoritm de învățare automată și este ușor de înțeles și implementat. Deci, ce este mai exact coborârea în gradient? Până la sfârșitul acestui articol, veți avea o înțelegere mai clară a algoritmului de coborâre a gradientului și a modului în care acesta poate fi utilizat pentru a actualiza parametrii modelului.

Coborâre în gradient

Înainte de a pătrunde adânc în algoritmul de coborâre a gradientului, ar trebui să știți ce este funcția de cost. Funcția de cost este o funcție utilizată pentru a măsura performanța modelului dvs. pentru un anumit set de date. Găsește diferența dintre valoarea estimată și valoarea așteptată, cuantificând astfel marja de eroare.

Scopul este de a reduce funcția de cost, astfel încât modelul să fie corect. Pentru a atinge acest obiectiv, trebuie să găsiți parametrii necesari în timpul antrenamentului modelului dvs. Coborârea gradientului este un astfel de algoritm de optimizare utilizat pentru a găsi coeficienții unei funcții pentru a reduce funcția de cost. Punctul în care funcția de cost este minimă este cunoscut sub numele de minime globale.

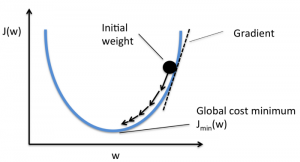
Sursă

Intuiția din spatele algoritmului Gradient Descent

Să presupunem că aveți un bol mare, asemănător cu ceva în care aveți fructele. Acest bol este graficul pentru funcția de cost. Fundul vasului este cel mai bun coeficient pentru care funcția de cost este minimă. Diferite valori sunt utilizate ca coeficienți pentru a calcula funcția de cost. Acest pas se repetă până când se găsesc cei mai buni coeficienți.

Vă puteți imagina coborârea în pante ca o minge care se rostogolește pe o vale. Valea este parcela pentru funcția de cost aici. Vrei ca mingea să ajungă la fundul văii, unde fundul văii reprezintă funcția de cel mai mic cost. În funcție de poziția de start a mingii, aceasta se poate sprijini pe multe funduri ale văii. Cu toate acestea, este posibil ca aceste funduri să nu fie cele mai joase puncte și sunt cunoscute ca minime locale.

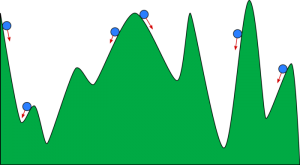
Sursă

Citiți: Îmbunătățirea învățării automate: ce este, funcții, tipuri și caracteristici

Algoritmul de coborâre a gradientului- Metodologie

Calculul coborârii gradientului începe cu valorile inițiale ale coeficienților pentru funcție fiind setate ca 0 sau o valoare mică aleatorie.

coeficient = 0 (sau o valoare mică)

• Funcția de cost se calculează punând această valoare a coeficientului în funcție.

Funcția de cost = f(coeficient)

• Știm din conceptul de calcul că derivata unei funcții este panta funcției. Calcularea pantei vă va ajuta să aflați direcția de mutare a valorilor coeficientului. Direcția ar trebui să fie astfel încât să obțineți un cost (eroare) mai mic în următoarea iterație.

del = derivat (funcția de cost)

• După ce cunoașteți direcția de coborâre din pantă, actualizați valorile coeficientului în consecință. O rată de învățare (alfa) poate fi selectată pentru a controla cât de mult se vor schimba acești coeficienți la fiecare iterație. Trebuie să vă asigurați că această rată de învățare nu este prea mare și nici prea scăzută.

coeficient = coeficient – ​​(alpha * del)

• Acest proces se repetă până când funcția de cost devine 0 sau foarte aproape de 0.

f(coeficient) = 0 (sau aproape de 0)

Selectarea ratei de învățare este importantă. Selectarea unei rate de învățare foarte mare poate depăși minimele globale. Dimpotrivă, o rată de învățare foarte scăzută te poate ajuta să atingi minimele globale, dar convergența este foarte lentă, luând multe iterații.

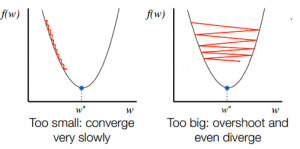
Sursă

Variante ale algoritmului de coborâre a gradientului

Coborâre în grad de lot

Coborârea gradientului în lot este una dintre cele mai utilizate variante ale algoritmului de coborâre a gradientului. Funcția de cost este calculată pe întregul set de date de antrenament pentru fiecare iterație. Un lot este denumit o iterație a algoritmului, iar această formă este cunoscută sub denumirea de coborâre a gradientului lotului.

Coborâre a gradientului stocastic

În unele cazuri, setul de antrenament poate fi foarte mare. În aceste cazuri, coborârea gradientului de lot va dura mult timp pentru a calcula, deoarece o iterație necesită o predicție pentru fiecare instanță din setul de antrenament. Puteți utiliza coborârea gradientului stocastic în aceste condiții în care setul de date este imens. În coborârea gradientului stocastic, coeficienții sunt actualizați pentru fiecare instanță de antrenament și nu la sfârșitul lotului de instanțe.

Coborâre cu gradient mini lot

Atât coborârea gradientului în lot, cât și coborârea gradientului stocastic au avantajele și dezavantajele lor. Cu toate acestea, poate fi utilă utilizarea unui amestec de coborâre a gradientului în lot și coborâre a gradientului stocastic. În coborârea gradientului mini-loturi, nici întregul set de date nu este utilizat și nici nu utilizați o singură instanță la un moment dat. Luați în considerare un grup de exemple de antrenament. Numărul de exemple din acest grup este mai mic decât întregul set de date, iar acest grup este cunoscut ca mini-lot.

Cele mai bune practici pentru algoritmul de coborâre a gradientului

• Hartă costul în funcție de timp: reprezentarea grafică a costului în funcție de timp vă ajută să vizualizați dacă costul scade sau nu după fiecare iterație. Dacă vedeți că costul rămâne neschimbat, încercați să actualizați rata de învățare.
• Rata de învățare: rata de învățare este foarte scăzută și este adesea selectată ca 0,01 sau 0,001. Trebuie să încerci să vezi care valoare funcționează cel mai bine pentru tine.
• Redimensionarea intrărilor: algoritmul de coborâre a gradientului va minimiza funcția de cost mai rapid dacă toate variabilele de intrare sunt redimensionate la același interval, cum ar fi [0, 1] sau [-1, 1].
• Mai puține treceri: de obicei, algoritmul de coborâre a gradientului stocastic nu are nevoie de mai mult de 10 treceri pentru a găsi cei mai buni coeficienți.

Consultați: 25 de întrebări și răspunsuri la interviu de învățare automată

Încheierea

Veți cunoaște rolul coborârii gradientului în optimizarea unui algoritm de învățare automată. Un factor important de reținut este alegerea ratei de învățare potrivite pentru algoritmul de coborâre a gradientului pentru o predicție optimă.

upGrad oferă o diplomă PG în Machine Learning și AI și un Master of Science în Machine Learning și AI, care vă poate ghida spre construirea unei cariere. Aceste cursuri vor explica necesitatea învățării automate și pașii suplimentari pentru a aduna cunoștințe în acest domeniu, acoperind concepte variate, de la algoritmi de coborâre a gradientului la rețele neuronale.