Grafici nella struttura dei dati: tipi, memorizzazione e attraversamento

Una struttura di dati è un modo efficiente di organizzare i dati nella scienza dei dati in modo che i dati possano essere facilmente accessibili e utilizzati in modo efficace. Esistono molti tipi di database, ma in questo articolo viene discusso il motivo per cui i grafici svolgono un ruolo fondamentale nella gestione dei dati.

Avviso spoiler: utilizzi i grafici nella struttura dei dati ogni giorno per recuperare la rotta migliore per il tuo ufficio, per ricevere suggerimenti per il tuo pranzo, film e per ottimizzare la rotta del tuo prossimo volo. Sembra interessante! Vediamo le proprietà del grafico e la sua applicazione.

Per prima cosa, vediamo cos'è un grafico? È una rappresentazione di dati in una struttura non lineare composta da nodi (o vertici) e bordi (o percorsi).

Un grafico nella struttura dati può essere definito come una struttura dati costituita da dati archiviati tra molti gruppi di bordi (percorsi) e vertici (nodi), che sono interconnessi. La struttura dei dati del grafico (N, E) è strutturata con una raccolta di nodi e bordi. Sia i nodi che i vertici devono essere finiti.

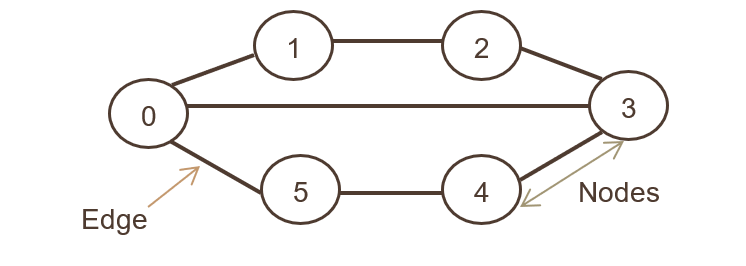
Nella rappresentazione grafica sopra, l'insieme dei nodi è N={0,1,2,3,4,5,6}e l'insieme degli spigoli è

G={01,12,23,34,45,05,03}

Ora studiamo i tipi di grafici.

Leggi: Le 10 migliori tecniche di visualizzazione dei dati

Tipi di grafici

1. Grafico ponderato

Grafici i cui bordi o percorsi hanno valori. Tutti i valori visti associati ai bordi sono chiamati pesi. Il valore dei bordi può rappresentare peso/costo/lunghezza.

Valori o pesi possono anche rappresentare:

• Distanza percorsa tra due punti- Es: per cercare il percorso più breve verso l'ufficio, la distanza tra due workstation in una rete di uffici.
• Velocità del pacchetto di dati in una rete o larghezza di banda.

2. Grafico non ponderato

Dove non vi è alcun valore o peso associato al bordo. Per impostazione predefinita, tutti i grafici non sono ponderati a meno che non sia associato un valore.

3. Grafico non orientato

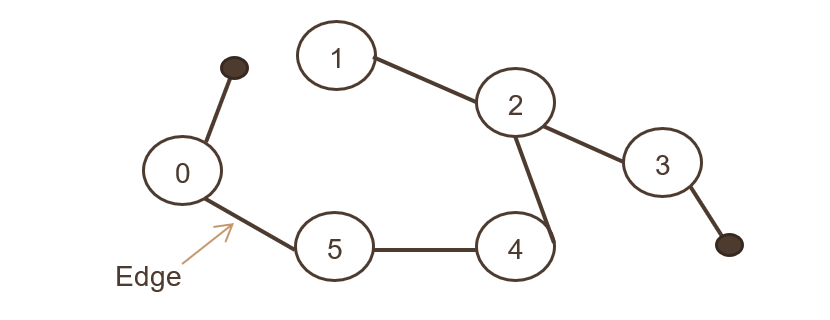
Dove un insieme di oggetti è connesso e tutti i bordi sono bidirezionali. L'immagine sotto mostra il grafico non orientato,

È come l'associatività di due utenti di Facebook dopo essersi collegati come amici. Entrambi gli utenti possono fare riferimento e condividere foto, commentare tra loro.

4. Grafico diretto

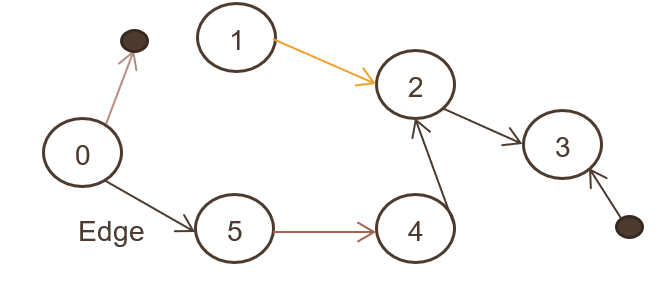
Chiamato anche digrafo, in cui un insieme di oggetti (N, E) è connesso e tutti i bordi sono diretti da un nodo all'altro. L'immagine sopra mostra il grafico diretto.

Checkout: progetti di visualizzazione dei dati che puoi replicare

Memorizzazione del grafico

Ogni metodo di archiviazione ha i suoi pro e contro e il metodo di archiviazione giusto viene scelto in base alla complessità. Le due strutture dati più comunemente utilizzate per memorizzare i grafici sono:

1. Elenco di adiacenze

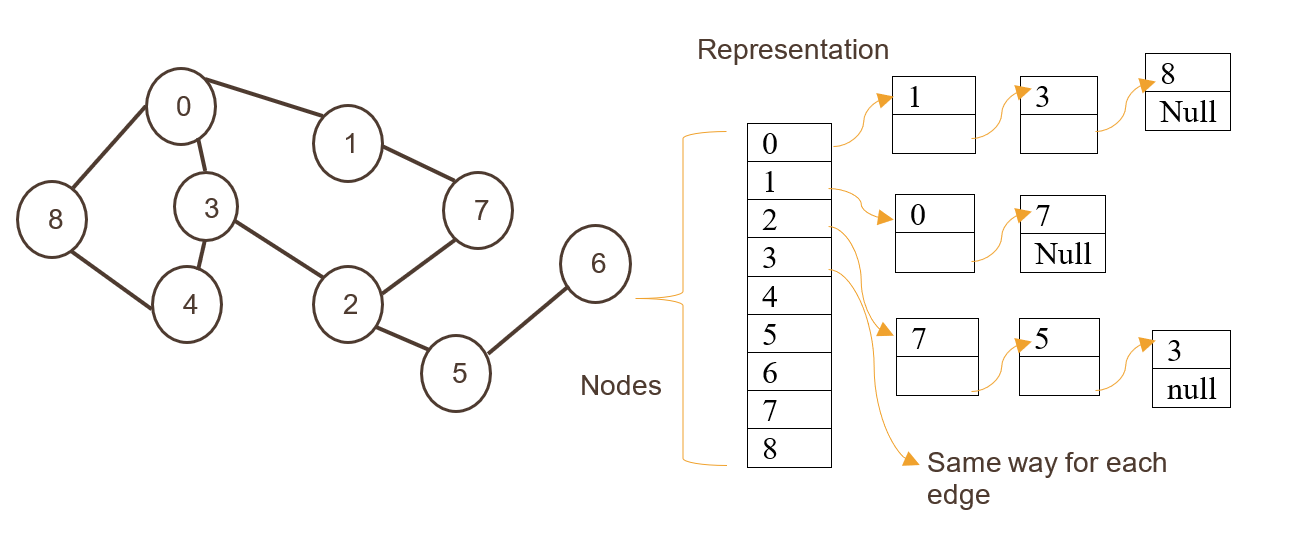
Qui i nodi vengono archiviati come un indice dell'array unidimensionale seguito da bordi archiviati come elenco.

2. Matrice di adiacenza

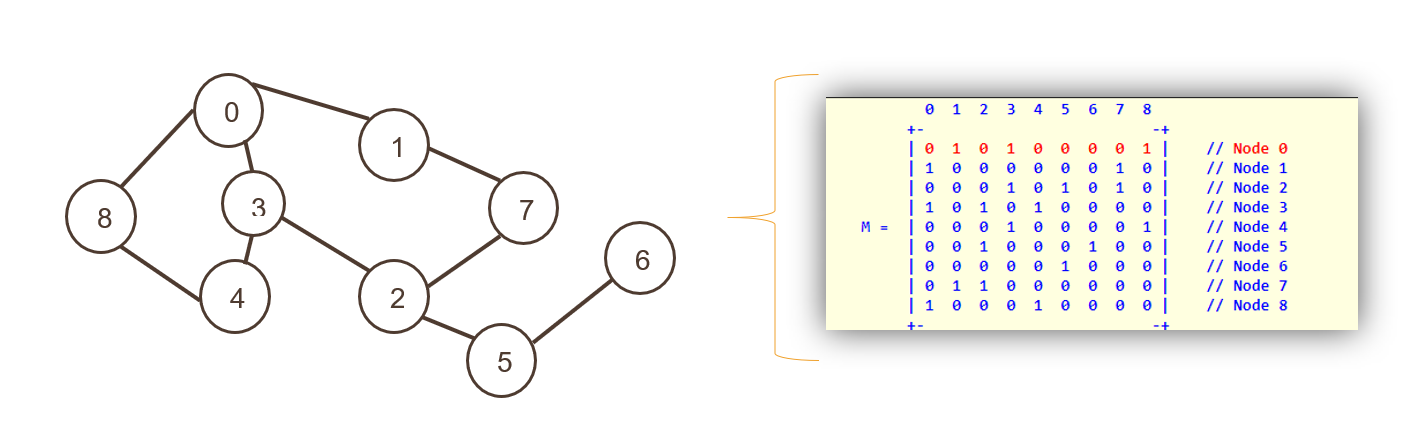
Qui i nodi sono rappresentati come l'indice di un array bidimensionale, seguito da bordi rappresentati come valori diversi da zero di una matrice adiacente.

Sia le righe che le colonne mostrano i nodi; l'intera matrice viene riempita con "0" o "1", che rappresenta vero o falso. Zero rappresenta che non esiste un percorso e 1 rappresenta un percorso.

Traversata del grafico

L'attraversamento del grafico è un metodo utilizzato per cercare i nodi in un grafico. L'attraversamento del grafico viene utilizzato per decidere l'ordine utilizzato per la disposizione dei nodi. Cerca anche gli spigoli senza creare un ciclo, il che significa che tutti i nodi e gli spigoli possono essere cercati senza creare un ciclo.

Ci sono due strutture di attraversamento del grafico.

1. DFS (Depth First Search): metodo di ricerca approfondita

La ricerca DFS inizia a partire dal primo nodo e va sempre più in profondità, esplorando fino a trovare il nodo di destinazione. Se la chiave di destinazione non viene trovata, il percorso di ricerca viene modificato nel percorso interrotto durante la ricerca iniziale e la stessa procedura viene ripetuta per quel ramo.

Lo spanning tree viene prodotto dal risultato di questa ricerca. Questo metodo ad albero è senza i loop. Il numero totale di nodi nella struttura dei dati dello stack viene utilizzato per implementare l'attraversamento DFS.

Passaggi seguiti per implementare la ricerca DFS:

Passaggio 1: la dimensione dello stack deve essere definita in base al numero totale di nodi.

Passaggio 2 – Selezionare il nodo iniziale per la trasversale; deve essere inserito nello stack visitando quel nodo.

Passaggio 3: ora, visita il nodo adiacente che non è stato visitato prima e inseriscilo nello stack.

Passaggio 4: ripetere il passaggio 3 finché non ci sono nodi adiacenti non visitati.

Passaggio 5: utilizzare il backtracking e un nodo quando non ci sono altri nodi da visitare.

Passaggio 6: svuotare la pila ripetendo i passaggi 3,4 e 5.

Passaggio 7: quando la pila è vuota, viene formato un albero di copertura finale eliminando i bordi inutilizzati.

Le applicazioni di DFS sono:

• Risolvere enigmi con una sola soluzione.
• Per verificare se un grafo è bipartito.
• Ordinamento topologico per la pianificazione del lavoro e molti altri.

2. BFS (Breadth-First Search): la ricerca viene implementata utilizzando un metodo di accodamento

La ricerca in ampiezza esplora un grafico con un movimento in ampiezza e utilizza in base alla coda per passare da un nodo all'altro, dopo aver incontrato una fine nel percorso.

Passi seguiti per implementare la ricerca BFS,

Passaggio 1 – In base al numero di nodi, viene definita la coda.

Passaggio 2: iniziare da qualsiasi nodo dell'attraversamento. Visita quel nodo e aggiungilo alla coda.

Passaggio 3: ora controlla il nodo adiacente non visitato, che si trova davanti alla coda, e aggiungilo alla coda, non all'inizio.

Passaggio 4: ora inizia a eliminare il nodo che non ha bordi che devono essere visitati e non è nella coda.

Passaggio 5: svuotare la coda ripetendo i passaggi 4 e 5.

Passaggio 6: rimuovere i bordi inutilizzati e formare lo spanning tree solo dopo che la coda è vuota.

Le applicazioni di BFS sono:

• Reti peer to peer: come in Bittorrent, viene utilizzato per trovare tutti i nodi adiacenti.
• Crawler nel motore di ricerca.
• Siti di social networking e molti altri.

Applicazioni reali del grafico nella struttura dei dati

I grafici vengono utilizzati in molte applicazioni quotidiane come la rappresentazione di rete (strade, mappatura di fibre ottiche, progettazione di circuiti stampati, ecc.). Es: nella rete dati di Facebook, i nodi rappresentano l'utente, la sua foto o il suo commento, e i bordi rappresentano le foto, i commenti sulla foto.

Il grafico nella struttura dei dati ha applicazioni estese. Alcuni di quelli notevoli sono:

• API Social Graph : è il modo principale in cui i dati vengono comunicati all'interno e all'esterno della piattaforma dei social media di Facebook. È un'API basata su HTTP, che viene utilizzata per eseguire query sui dati in modo programmatico, caricare foto e video, creare nuove storie e molte altre attività. È composto da nodi, bordi e campi; per interrogare, vengono utilizzati i nodi oggetto specifici. I bordi di un gruppo di oggetti soggetti a un singolo oggetto e i campi vengono utilizzati per recuperare i dati su ciascun oggetto nel gruppo.
• API GraphQL di Yelp : è un motore di suggerimenti utilizzato per recuperare i dati specifici dalla piattaforma Yelp. Qui, gli ordini vengono utilizzati per trovare i bordi, dopodiché viene interrogato il nodo specifico per recuperare il risultato esatto. Questo accelera il processo di recupero.

Sulla piattaforma Yelp, i nodi rappresentano l'azienda, contenente id, name, is_closed e molte altre proprietà del grafico.

• Algoritmi di ottimizzazione del percorso : vengono utilizzati per trovare la migliore connessione che soddisfi i criteri di velocità, sicurezza, carburante, ecc. BFS viene utilizzato in questo algoritmo. L'esempio migliore è Google Maps Platform (Maps, Routes APIs).
• Reti di volo: nelle reti di volo, viene utilizzato per trovare il percorso ottimizzato che si adatta alla struttura dei dati del grafico . Questo aiuta anche nel modello e ottimizza le procedure aeroportuali in modo efficiente.

Leggi anche: Vantaggi della visualizzazione dei dati

Conclusione

In questo articolo, abbiamo prima discusso la definizione di Graph e Graph nella struttura dei dati e poi abbiamo appreso i tipi di grafici con le loro proprietà. Successivamente, abbiamo appreso i metodi comunemente usati per la memorizzazione dei grafici seguiti da importanti metodi di ricerca di argomenti utilizzati in Grafici, Graph Traversal. Infine, abbiamo discusso le applicazioni nel mondo reale della struttura dei dati dei grafi.

Questo articolo ha fornito informazioni dettagliate sui grafici nella struttura dei dati ; la conoscenza di questo è vitale per la comprensione fondamentale nei database Graph, nell'implementazione dell'algoritmo di ricerca, nella programmazione e in molti altri. Deve essere appreso dall'esperto del settore.

Perché scegliere un corso con upGrad ?

Ti consigliamo di scegliere il programma Executive PG in Data Science offerto da IIIT Bangalore ospitato su upGrad perché qui puoi ottenere le tue domande 1-1 con gli istruttori del corso. Non si concentra solo sull'apprendimento teorico, ma dà importanza alla conoscenza pratica, che è essenziale per preparare gli studenti ad affrontare progetti del mondo reale e fornirti il ​​​​1° certificato NASSCOM dell'India, che ti aiuta a ottenere lavori ben pagati in Data Science.

Lavori citati

Dipartimento di Matematica/CS – Home , www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html.

"Intuizione matematica". Definizione del grafico diretto – Math Insight , mathinsight.org/definition/directed_graph.

Singh, Amritpal. "Struttura dei dati del grafico". Medio , Medio, 29 marzo 2020, medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3.

Assolo. "Le applicazioni reali delle strutture dati dei grafici che devi conoscere." Graph Data e GraphQL API Development-Leap Graph , leapgraph.com/graph-data-structures-applications.