Графики в структуре данных: типы, хранение и обход

Структура данных — это эффективный способ организации данных в науке о данных, чтобы к этим данным можно было легко получить доступ и эффективно использовать. Существует много типов баз данных, но в этой статье обсуждается, почему графы играют жизненно важную роль в управлении данными.

Внимание, спойлер: вы используете Графики в структуре данных каждый день, чтобы выбрать лучший маршрут до вашего офиса, получить предложения для вашего обеда, фильма и оптимизировать маршрут вашего следующего полета. Звучит интересно! Давайте посмотрим на свойства графа и его применение.

Во-первых, давайте посмотрим, что такое график? Это представление данных в виде нелинейной структуры, состоящей из узлов (или вершин) и ребер (или путей).

Граф в структуре данных можно назвать структурой данных, состоящей из данных, которые хранятся среди множества групп ребер (путей) и вершин (узлов), которые связаны между собой. Структура данных графа (N, E) состоит из набора узлов и ребер. И узлы, и вершины должны быть конечными.

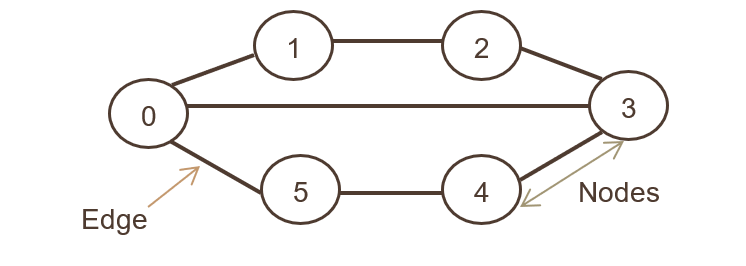
В приведенном выше представлении графа набор узлов равен N = {0,1,2,3,4,5,6}, а набор ребер равен

Г={01,12,23,34,45,05,03}

Теперь давайте изучим типы графиков.

Читайте: 10 лучших методов визуализации данных

Типы графиков

1. Взвешенный график

Графы, ребра или пути которых имеют значения. Все видимые значения, связанные с ребрами, называются весами. Значение Edges может представлять вес/стоимость/длину.

Значения или веса могут также представлять:

• Расстояние, пройденное между двумя точками. Например: для поиска кратчайшего пути к офису расстояние между двумя рабочими станциями в офисной сети.
• Скорость пакета данных в сети или пропускная способность.

2. Невзвешенный график

Где нет значения или веса, связанного с ребром. По умолчанию все графики являются невзвешенными, если нет связанного значения.

3. Неориентированный граф

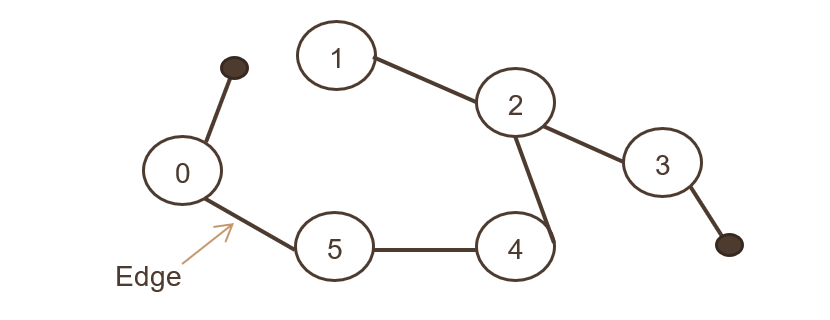
Где набор объектов соединен, и все ребра двунаправлены. На изображении ниже показан неориентированный граф,

Это похоже на ассоциативность двух пользователей Facebook после подключения в качестве друга. Оба пользователя могут ссылаться и обмениваться фотографиями, комментировать друг друга.

4. Направленный граф

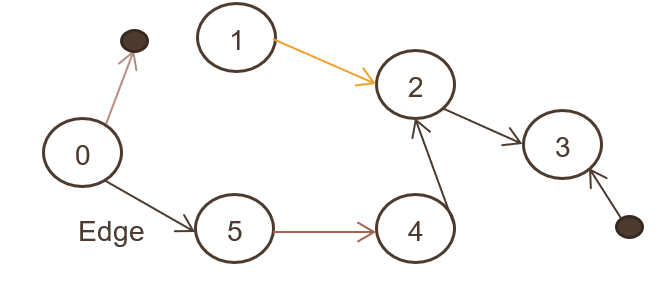
Также называется орграфом, где набор объектов (N, E) соединен, и все ребра направлены от одного узла к другому. На изображении выше показан ориентированный граф.

Оформить заказ: проекты визуализации данных, которые вы можете воспроизвести

Хранение графика

У каждого метода хранения есть свои плюсы и минусы, и правильный метод хранения выбирается в зависимости от сложности. Две наиболее часто используемые структуры данных для хранения графиков:

1. Список смежности

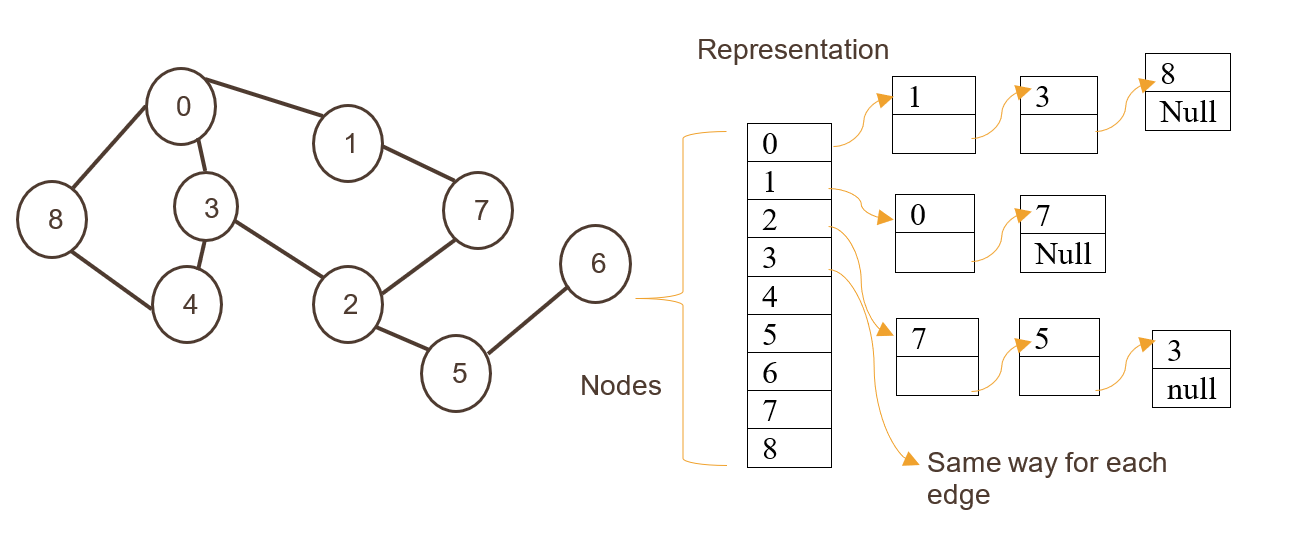
Здесь узлы хранятся как индекс одномерного массива, за которым следуют ребра, хранящиеся в виде списка.

2. Матрица смежности

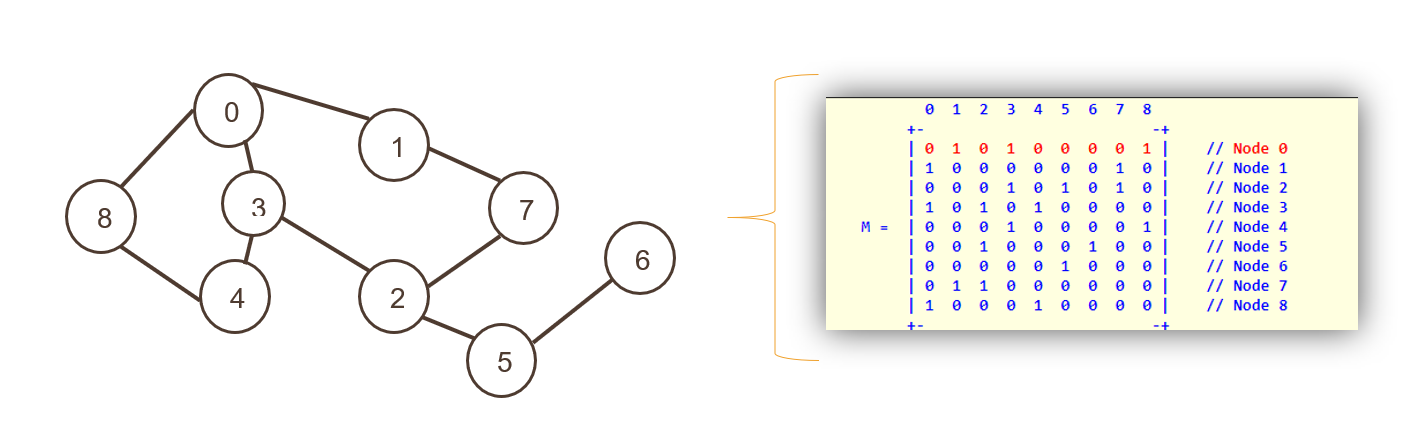
Здесь узлы представлены как индекс двумерного массива, за которым следуют ребра, представленные как ненулевые значения соседней матрицы.

И строки, и столбцы демонстрируют узлы; вся матрица заполняется либо «0», либо «1», представляющими истину или ложь. Ноль означает, что пути нет, а 1 — путь.

Обход графа

Обход графа — это метод, используемый для поиска узлов в графе. Обход графа используется для определения порядка расположения узлов. Он также ищет ребра без создания цикла, что означает, что все узлы и ребра можно искать без создания цикла.

Есть две структуры обхода графа.

1. DFS (поиск в глубину): метод углубленного поиска

Поиск DFS начинается с первого узла и идет все глубже и глубже, пока не будет найден целевой узел. Если целевой ключ не найден, путь поиска изменяется на путь, исследование которого было остановлено во время первоначального поиска, и та же процедура повторяется для этой ветви.

Связующее дерево создается из результата этого поиска. Этот метод дерева без циклов. Общее количество узлов в структуре данных стека используется для реализации обхода DFS.

Шаги, предпринятые для реализации поиска DFS:

Шаг 1. Размер стека необходимо определить в зависимости от общего количества узлов.

Шаг 2 – Выберите начальный узел для пересечения; его нужно поместить в стек, посетив этот узел.

Шаг 3. Теперь посетите соседний узел, который не посещался ранее, и поместите его в стек.

Шаг 4. Повторяйте шаг 3 до тех пор, пока не останется непосещенного соседнего узла.

Шаг 5 — Используйте возврат и один узел, когда нет других узлов, которые нужно посетить.

Шаг 6 — Очистите стек, повторив шаги 3, 4 и 5.

Шаг 7. Когда стек пуст, окончательное остовное дерево формируется путем исключения неиспользуемых ребер.

Приложения DFS:

• Решение головоломок только с одним решением.
• Чтобы проверить, является ли граф двудольным.
• Топологическая сортировка для планирования работы и многое другое.

2. BFS (поиск в ширину): поиск реализован с использованием метода очередей.

Поиск в ширину перемещает граф по ширине и использует очередь для перехода от одного узла к другому после обнаружения конца пути.

Шаги, предпринятые для реализации поиска BFS,

Шаг 1. В зависимости от количества узлов определяется очередь.

Шаг 2 – Начните с любого узла обхода. Посетите этот узел и добавьте его в очередь.

Шаг 3 — Теперь проверьте непосещаемый соседний узел, который находится перед очередью, и добавьте его в очередь, а не в начало.

Шаг 4. Теперь начните удалять узел, у которого нет ребер, которые нужно посетить, и который не находится в очереди.

Шаг 5 – Очистите очередь, повторив шаги 4 и 5.

Шаг 6 — Удалите неиспользуемые ребра и сформируйте остовное дерево только после того, как очередь опустеет.

Приложения BFS:

• Одноранговые сети. Как и в Bittorrent, он используется для поиска всех соседних узлов.
• Сканеры в поисковой системе.
• Сайты социальных сетей и многое другое.

Реальные приложения графа в структуре данных

Графики используются во многих повседневных приложениях, таких как представление сети (дороги, картирование оптоволокна, проектирование печатных плат и т. д.). Пример: в сети данных Facebook узлы представляют пользователя, его/ее фотографию или комментарий, а ребра представляют фотографии, комментарии к фотографии.

Граф в структуре данных имеет обширные приложения. Некоторые из примечательных:

• API-интерфейсы Social Graph — это основной способ передачи данных в платформу социальных сетей Facebook и за ее пределы. Это API на основе HTTP, который используется для программного запроса данных, загрузки фотографий и видео, создания новых историй и многих других задач. Он состоит из узлов, ребер и полей; для запроса используются определенные узлы объекта. Ребра для группы объектов, подчиненных одному объекту и полям, используются для получения данных о каждом объекте в группе.
• API Yelp GraphQL — это система рекомендаций, используемая для получения конкретных данных с платформы Yelp. Здесь порядок используется для поиска ребер, после чего запрашивается конкретный узел для получения точного результата. Это ускоряет процесс поиска.

На платформе Yelp узлы представляют бизнес, содержащие идентификатор, имя, is_closed и многие другие свойства графа.

• Алгоритмы оптимизации пути . Они используются для поиска наилучшего соединения, которое соответствует критериям скорости, безопасности, топлива и т. д. В этом алгоритме используется BFS. Лучшим примером является платформа Google Maps (карты, Routes API).
• Flight Networks — в полетных сетях это используется для поиска оптимизированного пути, который соответствует структуре данных графа . Это также помогает модели и эффективно оптимизирует процедуры в аэропорту.

Читайте также: Преимущества визуализации данных

Заключение

В этой статье мы сначала обсудили определение Graph и Graph в структуре данных, а затем узнали о типах графов и их свойствах. Позже мы узнали о часто используемых методах хранения графиков, а затем о важных методах поиска тем, используемых в Graphs, Graph Traversal. Наконец, мы обсудили реальные приложения структуры данных графа.

Эта статья предоставила информацию о графиках в структуре данных ; знание этого жизненно важно для фундаментального понимания баз данных Graph, реализации алгоритмов поиска, программирования и многого другого. Это нужно узнавать у отраслевого эксперта.

Почему стоит выбрать курс с upGrad ?

Мы рекомендуем вам выбрать программу Executive PG в области науки о данных , предлагаемую IIIT Bangalore, размещенную на upGrad, потому что здесь вы можете получить свои вопросы 1-1 с преподавателями курса. Он фокусируется не только на теоретическом обучении, но и придает большое значение практическим знаниям, которые необходимы для подготовки учащихся к работе с реальными проектами и предоставления вам первого в Индии сертификата NASSCOM, который поможет вам получить высокооплачиваемую работу в науке о данных.

Процитированные работы

Факультет математики/CS – Домашняя страница , www.mathcs.emory.edu/~cheung/Courses/171/Syllabus/11-Graph/data-stru.html.

«Математическое понимание». Определение направленного графа — Math Insight , mathinsight.org/definition/directed_graph.

Сингх, Амритпал. «Структура графических данных». Medium , Medium, 29 марта 2020 г., medium.com/@singhamritpal49/graph-data-structure-49427c81b3b3.

Соло. «Реальные приложения графических структур данных, которые вы должны знать». Графические данные и разработка GraphQL API — Leap Graph , jumpgraph.com/graph-data-structures-applications.