什么是算法博弈论？ 举例说明

1999 年，当 Nisan 和 Ronen 将他们的想法贡献给一篇论文时，世界见证了一个新的算法机制设计概念。 它试图否定无政府状态的代价，在这种情况下，自利总是导致系统退化。

他们的论文证明，多个自利方可以建立一个均衡的生产系统。 因此，我们不会着眼于退化的经济，而是着眼于社会福利和收入最大化。

算法博弈论（AGT）是基于对算法机制设计（AMD）的理解。

虽然 AMD 描述了自利可以导致一个好的系统，但 AGT 旨在分析和设计一个描述自利参与者行为的战略设置。

在我们了解 AGT 在战略环境中如何运作之前，让我们先看看博弈论是如何运作的！

让我们借助一个例子来理解博弈论

在一个完美的世界里，每一步都是经过精心计算的，博弈论不会像今天这样有意义。

计算聪明、理性的公民下一步行动的想法既令人兴奋又令人恐惧。

博弈论规定，在任何给定的社会情况下，竞争方都可以通过评估可能性的有效性和估计竞争对手的净移动来做出理性决策。

虽然这看起来像是一场赌博，但理论家们已经恢复了一种可以解释的策略，从而根除人们认为这是一场赌博的信念。

最常见的例子是囚徒困境。

学习：每个开发人员都应该尝试的前 8 个项目

囚徒困境解释

前提很简单——当警察抓到两名罪犯并询问他们的罪行时，他们都不会打破他们的沉默。

因此，DA 决定通过在他们面前提出三个条件来简化这一点，因为他们坐在相邻的位置。

• 条件一：如果两人都不供认罪行，则入狱六年。
• 条件2：如果其中一只老鼠出卖另一只老鼠，举报人可以自由漫游，而另一只老鼠进入十年。
• 条件三：如果双方都认罪，则入狱一年。

在听取了条件后，他们立即被带到一个单独的房间做出决定。

我们可以像这样以矩阵的形式传输这些数据；

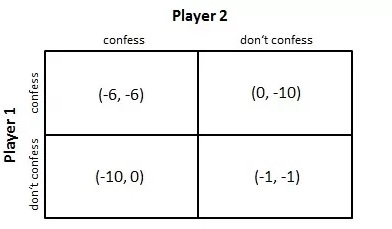
资源

这个问题的解决方案很简单；

每个囚犯都会考虑说出罪行的真相。 两人都不能严格说对方会保持沉默。 所以，屈服于可能性，他们俩都决定认罪，只入狱一年。

博弈论是掌握它的有力武器。 通过了解数字的性质和社会设置位置，我们甚至可以破译最复杂的情​​况。

算法博弈论

现在，考虑博弈论和计算机科学的维恩图。 想象一下，为什么要绘制实现答案的概率图表的准确性水平会急剧提高。

这就是算法博弈论（AGT）所做的！

它试图通过在计算机算法和博弈论之间取得完美平衡来解决现代问题。

用更简单的话来说，算法博弈论试图定义执行任务之间的社会经济平衡。 它还使用了纳什均衡的原理； 它指出，一旦参与者找到适合他们的策略，他们将不希望偏离它，直到它不再对他们有利。

让我们举一个小例子来了解算法博弈论的工作原理。

当我们玩 Kho-Kho、Ice & Water、Chain-Cut 等游戏时，让我们回到学校。这些游戏中的每一个都有精美的设计和可玩的机制。

例如，让我们考虑一下冰与水；

• 有几名球员和一名接球手。 捕手应该把每个人都变成冰。
• 其他玩家有能力在触碰某人时将其变回水。
• 有自由区，玩家可以休息 30 秒。

现在，如果你仔细看，你会发现这些规则中的每一个都构成了游戏的机制并定义了它的设计。

• 玩家可以玩这个游戏，只要他们觉得有趣。 在这里，纳什均衡描述了只要玩家发现他们的策略有效并且游戏有趣，他们就会玩。
• 玩家的口粮是不被抓住。 她通过了解设置来执行该配给。 她实施了一种目标至上的方法，在这种方法中，她通过不被抓住来赢得比赛。 这通常被称为机制设计或反向博弈论。
• 现在，如果每个玩家只考虑一个动机——“不被抓住”——而不考虑它的第二部分——“拯救其他玩家”，那么这个概念被称为无政府状态的代价。 它解释了任何系统的效率将如何由于玩家的自私行为而降低。

现在，从上面提到的三个概念中出现了更多的概念。 虽然它们都与博弈论完全或适度相关，但它们为算法博弈论创造了功能基础。

结帐： 42个令人兴奋的Python项目想法和初学者主题

现在，问题出现了：“我们如何用算法来表示战略环境？”

现在让我们看看如何使用 Python 定义战略环境并了解 Nashpy 在给定情况下的实现。

想象一下，你正在和你的一个朋友玩剪刀石头布游戏。 你们每个人都有以下三个选项之一；

• 岩石
• 纸
• 剪刀

赢得比赛的标准是

• 石头压碎剪刀
• 剪刀剪纸
• 纸盖岩石

这意味着，如果两名球员都表现出色，那就是重头戏。

我们可以用 3×3 矩阵的形式表示，其中 Aij 是；

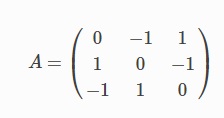
资源

注意：这里，i 和 j 是两个玩家的回合。

这里，

• 零表示你们两个都玩同一个对象（摇滚乐；或纸纸）
• 一个代表你们中的一个胜过另一个（就像石头剪刀布一样）
• 减一代表你们中的任何一个输了，因为另一个胜过你（就像石头纸一样）

现在，为了在 Nashpy 上表示这一点，您将编写一个看起来像这样的代码；

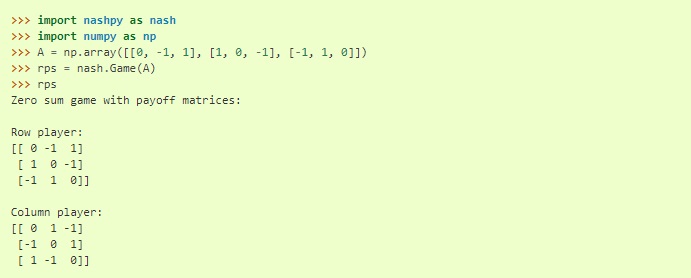
资源

最后的想法

算法博弈论是当今世界的一个完美原则，竞争源于利己，胜利是利己的成就。

因此，作为现代管理者、教师、CXO 或商人，如果您了解算法博弈论的主导地位，那么请允许我更改《哈利·波特》中西弗勒斯·斯内普的名言；

“算法博弈论可以教你如何限制名声、酿造荣耀，甚至阻止损失。”

了解算法博弈论可以帮助您比以往更果断地处理数字。 在当前时代，我们决定最后的细节以制定可持续计划，AGT 被证明是一个转型方面。

我们已经知道数据科学可以将企业转变为利润丰厚的领域，但 AGT 有能力提高门槛。

假设您仍然对博弈论以及数据科学如何成为当今最赚钱和最具竞争力的职业持怀疑态度。

如果您想了解数据科学，请查看 IIIT-B 和 upGrad 的数据科学 PG 文凭，该文凭专为在职专业人士而设，提供 10 多个案例研究和项目、实用的实践研讨会、与行业专家的指导、1-与行业导师面对面交流，400 多个小时的学习和顶级公司的工作协助。