Qu'est-ce que la théorie algorithmique des jeux ? Expliqué avec des exemples

En 1999, lorsque Nisan et Ronen ont apporté leurs idées à un article, le monde a été témoin d'un nouveau concept de conception de mécanisme algorithmique. Il tente de nier le prix de l'anarchie, où l'intérêt personnel se traduit toujours par un système dégradé.

Leur article a prouvé que plusieurs parties intéressées pouvaient établir un système productif à l'équilibre. Ainsi, au lieu de regarder une économie en dégradation, nous nous pencherions sur le bien-être social et la maximisation des revenus.

La théorie algorithmique des jeux (AGT) est basée sur la compréhension de la conception de mécanismes algorithmiques (AMD) .

Alors qu'AMD décrit que l'intérêt personnel pourrait conduire à un bon système, AGT vise à analyser et à concevoir une configuration stratégique qui décrit les actions des participants intéressés.

Avant d'examiner comment l'AGT fonctionne dans l'environnement stratégique, regardons comment fonctionne la théorie des jeux !

Comprenons la théorie des jeux à l'aide d'un exemple

Dans un monde parfait, où chaque mouvement est un effort calculé, la théorie des jeux n'aurait pas autant de sens qu'aujourd'hui.

L'idée de calculer le prochain mouvement de citoyens intelligents et rationnels est à la fois passionnante et effrayante.

La théorie des jeux stipule que dans toute situation sociale donnée, les parties en compétition peuvent prendre des décisions rationnelles en évaluant la validité des possibilités et en estimant le mouvement net du concurrent.

Bien que cela puisse ressembler à un pari, les théoriciens ont rétabli une stratégie explicable qui déracine la croyance qu'il s'agit d'un pari.

L'exemple le plus souvent mentionné est le dilemme du prisonnier.

Apprendre : Les 8 meilleurs projets que chaque développeur devrait essayer sans échec

Le dilemme du prisonnier expliqué

La prémisse est simple - lorsque la police a attrapé deux condamnés et les a interrogés sur le crime, aucun des deux n'a rompu leur silence.

Ainsi, le DA a décidé de simplifier cela en établissant trois conditions devant eux, car ils sont assis de manière adjacente.

• Condition 1 : Si aucun d'eux n'avoue le crime, ils vont en prison pour six ans.
• Condition 2 : Si l'un dénonce l'autre, le lanceur d'alerte peut se déplacer librement tandis que l'autre reste pendant dix ans.
• Condition 3 : Si les deux avouent, ils vont en prison pour un an.

Immédiatement après avoir écouté les conditions, ils sont emmenés dans une pièce séparée pour prendre leurs décisions.

Nous pouvons transférer ces données sous la forme d'une matrice, en tant que telle ;

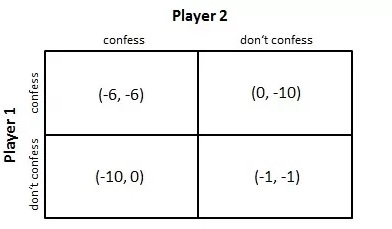
La source

La solution à ce problème est simple;

Chaque prisonnier envisagera de dire la vérité sur le crime. Aucun des deux ne peut strictement dire que l'autre restera silencieux. Alors, cédant à la probabilité, tous deux décident d'avouer le crime et n'iront en prison que pour un an.

La théorie des jeux est une arme puissante entre les mains de celui qui la manie. Nous pouvons déchiffrer même les situations les plus complexes en comprenant la nature des nombres et le placement social.

Théorie algorithmique des jeux

Maintenant, considérons un diagramme de Venn de la théorie des jeux et de l'informatique. Imaginez une augmentation drastique du niveau de précision pourquoi tracer la probabilité d'obtenir des réponses.

Et c'est ce que fait la théorie algorithmique des jeux (AGT) !

Il tente de résoudre les problèmes d'aujourd'hui en trouvant un équilibre parfait entre les algorithmes informatiques et la théorie des jeux.

En termes plus simples, la théorie algorithmique des jeux tente de définir l'équilibre socio-économique entre l'exécution d'une tâche. Il utilise également les principes de l'équilibre de Nash ; il stipule qu'une fois que les participants ont trouvé une stratégie qui fonctionne pour eux, ils ne souhaiteront pas s'en écarter jusqu'à ce qu'elle cesse de fonctionner à leur avantage.

Prenons un petit exemple pour comprendre le fonctionnement de la théorie algorithmique des jeux.

Revenons à l'école lorsque nous avons joué à des jeux comme Kho-Kho, Ice & Water, Chain-Cut, etc. Chacun de ces jeux a un beau design et un mécanisme à jouer.

Considérons Ice & Water, par exemple;

• Il y a plusieurs joueurs et un receveur. Le receveur est censé transformer tout le monde en glace.
• Les autres joueurs ont le pouvoir de retourner quelqu'un à l'eau en le touchant.
• Il existe des zones libres où les joueurs peuvent se reposer pendant 30 secondes.

Maintenant, si vous regardez attentivement, vous verrez que chacune de ces règles constitue le mécanisme du jeu et définit sa conception.

• Les joueurs peuvent jouer à ce jeu aussi longtemps qu'ils le trouvent intéressant. Ici, The Nash Equilibria décrit que tant que les joueurs trouvent que leur stratégie fonctionne et que le jeu est intéressant, ils doivent jouer.
• La ration d'un joueur est de ne pas se faire prendre. Et elle agit sur cette ration en comprenant la configuration. Elle met en œuvre une approche objective d'abord, où elle gagne le jeu en ne se faisant pas prendre. Et ceci est connu sous le nom de conception de mécanismes ou théorie des jeux inversés.
• Maintenant, dans le cas où chaque joueur ne considère qu'un seul motif – « ne pas se faire prendre » – et ne considère pas la deuxième partie – « sauver les autres joueurs », alors ce concept s'appelle le prix de l'anarchie. Il explique comment l'efficacité de tout système se dégradera en raison des comportements égoïstes des joueurs.

Maintenant, une pléthore de concepts supplémentaires émergent des trois concepts mentionnés ci-dessus. Bien qu'ils soient tous entièrement ou modérément liés à la théorie des jeux, ils créent une base fonctionnelle pour la théorie algorithmique des jeux.

Checkout : 42 idées et sujets de projets Python passionnants pour les débutants

Maintenant, la question se pose : « Comment représenter un environnement stratégique en termes d'Algorithmes ?

Voyons maintenant comment nous pouvons utiliser Python pour définir un environnement stratégique et comprendre l'implémentation de Nashpy pour une situation donnée.

Imaginez que vous jouez à une partie de pierre-papier-ciseaux avec un de vos amis. Chacun de vous a l'une des trois options ;

• Roche
• Papier
• Les ciseaux

Et la rubrique pour gagner le jeu est

• La pierre écrase les ciseaux
• Les ciseaux coupent les papiers
• Le papier recouvre la roche

Et cela signifie que si les deux joueurs présentent du rock, cela représente des reprises.

Nous pouvons représenter cela sous la forme d'une matrice 3×3 où Aij est ;

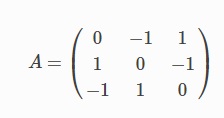
La source

Remarque : Ici, i et j sont les tours joués par les deux joueurs.

Ici,

• Zéro signifie que vous avez tous les deux joué le même objet (rock-rock ; ou papier-papier)
• L'un représente que l'un de vous l'a emporté sur l'autre (comme des ciseaux à pierre)
• Moins un représente que l'un de vous a perdu parce que l'autre vous a surpassé (comme du papier de roche)

Maintenant, pour représenter ceci sur Nashpy, vous allez écrire un code qui ressemble à ceci ;

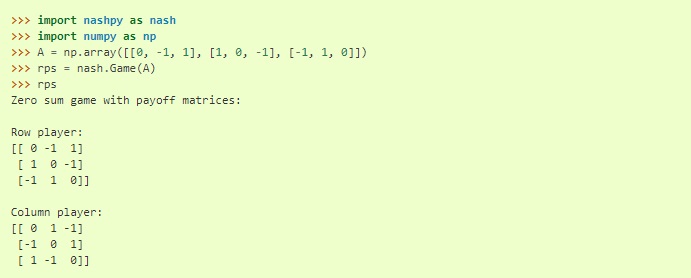
La source

Dernières pensées

La théorie algorithmique des jeux est un principe parfait dans le monde actuel où la concurrence découle de l'intérêt personnel, et la victoire est l'accomplissement de l'intérêt personnel.

Donc, en tant que managers, enseignants, CXO ou hommes d'affaires modernes, si vous comprenez la domination de la théorie algorithmique des jeux, alors permettez-moi de modifier la citation de Severus Rogue de Harry Potter ;

"La théorie algorithmique des jeux peut vous apprendre à embouteiller la renommée, à infuser la gloire, et même à stopper les pertes."

Comprendre la théorie algorithmique des jeux peut vous aider à gérer les nombres de manière plus décisive que jamais. À l'ère actuelle, où nous décidons les choses dans les moindres détails pour développer un plan durable, AGT s'avère être un aspect transformationnel.

Nous savons déjà que la science des données peut transformer les entreprises en une arène lucrative, mais AGT a le pouvoir de relever le seuil.

Supposons que vous soyez toujours sceptique quant à la théorie des jeux et à la façon dont la science des données est la profession la plus lucrative et la plus compétitive aujourd'hui.

Si vous êtes curieux d'en savoir plus sur la science des données, consultez le diplôme PG de IIIT-B & upGrad en science des données qui est créé pour les professionnels en activité et propose plus de 10 études de cas et projets, des ateliers pratiques, un mentorat avec des experts de l'industrie, 1- on-1 avec des mentors de l'industrie, plus de 400 heures d'apprentissage et d'aide à l'emploi avec les meilleures entreprises.