您應該了解的機器學習中的 6 種回歸模型

介紹

線性回歸和邏輯回歸是兩種類型的回歸分析技術，用於使用機器學習解決回歸問題。 它們是最突出的回歸技術。 但是，機器學習中有許多類型的回歸分析技術，它們的使用根據所涉及數據的性質而有所不同。

本文將解釋機器學習中不同類型的回歸，以及在什麼條件下可以使用它們。 如果你是機器學習的新手，這篇文章肯定會幫助你理解回歸建模的概念。

什麼是回歸分析？

回歸分析是一種預測建模技術，用於分析數據集中目標或因變量與自變量之間的關係。 當目標變量和自變量之間顯示出線性或非線性關係，並且目標變量包含連續值時，就會使用不同類型的回歸分析技術。 回歸技術主要用於確定預測變量的強度、預測趨勢、時間序列以及因果關係。

回歸分析是使用數據建模解決機器學習中回歸問題的主要技術。 它涉及確定最佳擬合線，這是一條穿過所有數據點的線，使得線與每個數據點的距離最小化。

回歸分析技術的類型

回歸分析技術有很多種，每種方法的使用取決於因素的數量。 這些因素包括目標變量的類型、回歸線的形狀和自變量的數量。

以下是不同的回歸技術：

1. 線性回歸
2. 邏輯回歸
3. 嶺回歸
4. 套索回歸
5. 多項式回歸
6. 貝葉斯線性回歸

下面詳細解釋機器學習技術中不同類型的回歸：

1. 線性回歸

線性回歸是機器學習中最基本的回歸類型之一。 線性回歸模型由相互線性相關的預測變量和因變量組成。 如果數據涉及多個自變量，則線性回歸稱為多元線性回歸模型。

下面給出的方程用於表示線性回歸模型：

y=mx+c+e

其中 m 是直線的斜率，c 是截距，e 表示模型中的誤差。

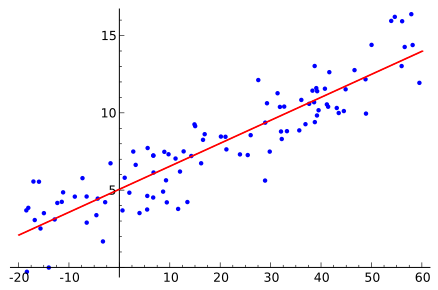
資源

最佳擬合線是通過改變 m 和 c 的值來確定的。 預測誤差是觀測值與預測值之間的差值。 m 和 c 的值以給出最小預測誤差的方式選擇。 需要注意的是，簡單的線性回歸模型容易受到異常值的影響。 因此，不應在大數據的情況下使用它。

2. 邏輯回歸

邏輯回歸是回歸分析技術的一種，當因變量是離散的時使用。 示例：0 或 1，真或假等。這意味著目標變量只能有兩個值，而 sigmoid 曲線表示目標變量和自變量之間的關係。

Logit 函數在 Logistic 回歸中用於衡量目標變量與自變量之間的關係。 下面是表示邏輯回歸的方程。

logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3….+bkXk

其中 p 是特徵出現的概率。

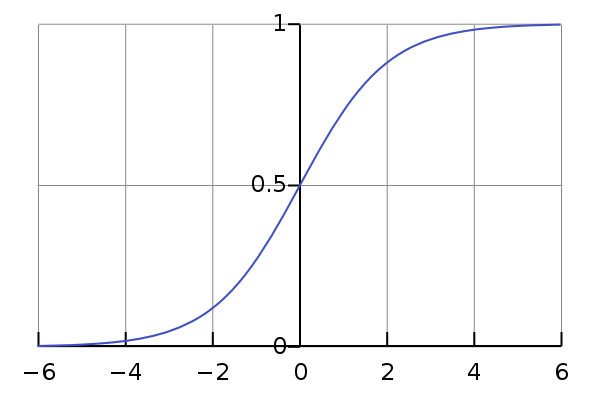
資源

對於選擇邏輯回歸，作為回歸分析技術，應該注意，數據量很大，目標變量中出現的值幾乎相等。 此外，不應存在多重共線性，這意味著數據集中的自變量之間不應存在相關性。

3. 嶺回歸

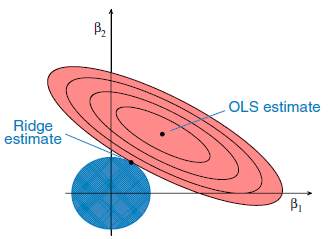
資源

這是機器學習中的另一種回歸類型，通常在自變量之間存在高度相關性時使用。 這是因為，在多共線數據的情況下，最小二乘估計會給出無偏值。 但是，如果共線性非常高，可能會有一些偏差值。 因此，在嶺回歸方程中引入了一個偏置矩陣。 這是一種強大的回歸方法，模型不易過度擬合。

下面是用於表示嶺回歸的方程，其中引入 λ (lambda) 解決了多重共線性問題：

β = (X^{T}X + λ*I)^{-1}X^{T}y

查看：機器學習的 5 個突破性應用

4. 套索回歸

套索回歸是機器學習中的一種回歸類型，它與特徵選擇一起執行正則化。 它禁止回歸係數的絕對大小。 結果，係數值接近於零，這在嶺回歸的情況下不會發生。

因此，Lasso Regression 中使用了特徵選擇，它允許從數據集中選擇一組特徵來構建模型。 在 Lasso Regression 的情況下，僅使用所需的特徵，而其他特徵為零。 這有助於避免模型中的過度擬合。 如果自變量高度共線，那麼 Lasso 回歸只選擇一個變量，並使其他變量縮小到零。

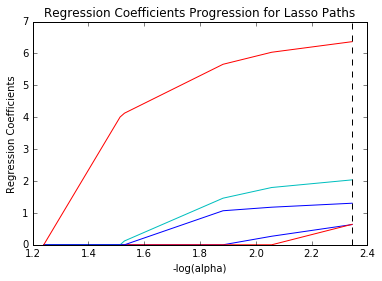
資源

下面是代表 Lasso 回歸方法的方程：

N^{-1}Σ^{N}_{i=1}f(x_{i}, y_{I}, α, β)

5. 多項式回歸

多項式回歸是機器學習中的另一種回歸分析技術，它與多元線性回歸相同，只是稍作修改。 在多項式回歸中，自變量和因變量之間的關係，即 X 和 Y，用 n 次表示。

它是作為估計量的線性模型。 最小均方法也用於多項式回歸。 多項式回歸中穿過所有數據點的最佳擬合線不是直線，而是曲線，這取決於 X 的冪或 n 的值。

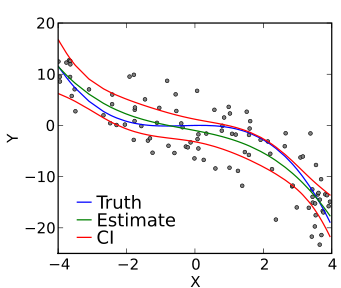
資源

在嘗試將均方誤差降至最低並獲得最佳擬合線時，該模型可能容易過度擬合。 建議對曲線進行分析，因為較高的多項式可能會在外推時給出奇怪的結果。

下面的等式代表多項式回歸：

l = β0+ β0x1+ε

閱讀：機器學習項目理念

6.貝葉斯線性回歸

貝葉斯回歸是機器學習中的一種回歸類型，它使用貝葉斯定理找出回歸係數的值。 在這種回歸方法中，確定特徵的後驗分佈而不是尋找最小二乘。 貝葉斯線性回歸類似於線性回歸和嶺回歸，但比簡單的線性回歸更穩定。

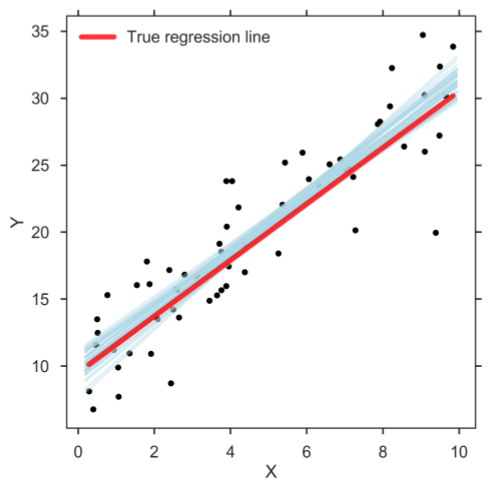
資源

從世界頂級大學在線學習AI 和 ML 課程- 碩士、高級管理人員研究生課程和 ML 和 AI 高級證書課程，以加快您的職業生涯。

結論

除了上述回歸方法外，機器學習中還有很多其他類型的回歸，包括彈性網絡回歸、JackKnife 回歸、逐步回歸和生態回歸。

這些不同類型的回歸分析技術可用於構建模型，具體取決於可用數據的類型或提供最大準確度的數據。 您可以更多地探索這些技術，也可以通過我們網站上的監督學習課程進行學習。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和 AI 執行 PG 計劃，該計劃專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT -B 校友身份，5 個以上實用的實踐頂點項目和頂級公司的工作協助。