6 Arten von Regressionsmodellen im maschinellen Lernen, die Sie kennen sollten

Einführung

Lineare Regression und logistische Regression sind zwei Arten von Regressionsanalysetechniken , die verwendet werden, um das Regressionsproblem mithilfe von maschinellem Lernen zu lösen. Sie sind die bekanntesten Techniken der Regression. Es gibt jedoch viele Arten von Regressionsanalysetechniken beim maschinellen Lernen, und ihre Verwendung variiert je nach Art der betroffenen Daten.

In diesem Artikel werden die verschiedenen Arten der Regression beim maschinellen Lernen erläutert und unter welchen Bedingungen sie jeweils verwendet werden können. Wenn Sie mit maschinellem Lernen noch nicht vertraut sind, wird Ihnen dieser Artikel sicherlich dabei helfen, das Konzept der Regressionsmodellierung zu verstehen.

Was ist Regressionsanalyse?

Die Regressionsanalyse ist eine prädiktive Modellierungstechnik, die die Beziehung zwischen dem Ziel oder der abhängigen Variablen und der unabhängigen Variablen in einem Datensatz analysiert. Die verschiedenen Arten von Regressionsanalysetechniken werden verwendet, wenn die Zielvariablen und die unabhängigen Variablen eine lineare oder nichtlineare Beziehung zueinander aufweisen und die Zielvariable kontinuierliche Werte enthält. Die Regressionstechnik wird hauptsächlich verwendet, um die Prädiktorstärke, den Prognosetrend, Zeitreihen und im Fall von Ursache-Wirkungs-Beziehungen zu bestimmen.

Die Regressionsanalyse ist die primäre Technik zur Lösung der Regressionsprobleme beim maschinellen Lernen mithilfe von Datenmodellierung. Es beinhaltet die Bestimmung der am besten passenden Linie, die eine Linie ist, die alle Datenpunkte so durchläuft, dass der Abstand der Linie von jedem Datenpunkt minimiert wird.

Arten von Regressionsanalysetechniken

Es gibt viele Arten von Regressionsanalysetechniken , und die Verwendung jeder Methode hängt von der Anzahl der Faktoren ab. Zu diesen Faktoren gehören die Art der Zielvariablen, die Form der Regressionslinie und die Anzahl der unabhängigen Variablen.

Nachfolgend sind die verschiedenen Regressionstechniken aufgeführt:

1. Lineare Regression
2. Logistische Regression
3. Ridge-Regression
4. Lasso-Regression
5. Polynomiale Regression
6. Bayessche lineare Regression

Die verschiedenen Arten der Regression in maschinellen Lernverfahren werden im Folgenden im Detail erläutert:

1. Lineare Regression

Die lineare Regression ist eine der grundlegendsten Regressionsarten beim maschinellen Lernen . Das lineare Regressionsmodell besteht aus einer Prädiktorvariablen und einer abhängigen Variablen, die linear zueinander in Beziehung stehen. Falls die Daten mehr als eine unabhängige Variable umfassen, wird die lineare Regression als multiple lineare Regressionsmodelle bezeichnet.

Die unten angegebene Gleichung wird verwendet, um das lineare Regressionsmodell zu bezeichnen:

y=mx+c+e

Dabei ist m die Steigung der Geraden, c ein Schnittpunkt und e der Fehler im Modell.

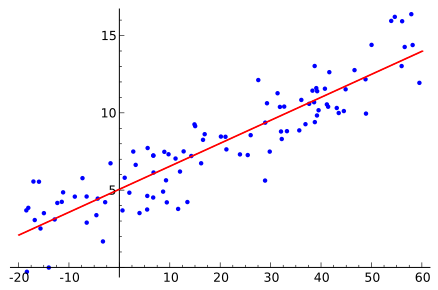
Quelle

Die am besten passende Linie wird bestimmt, indem die Werte von m und c variiert werden. Der Prädiktorfehler ist die Differenz zwischen den beobachteten Werten und dem vorhergesagten Wert. Die Werte von m und c werden so gewählt, dass sie den minimalen Prädiktorfehler ergeben. Es ist wichtig zu beachten, dass ein einfaches lineares Regressionsmodell anfällig für Ausreißer ist. Daher sollte es nicht bei großen Datenmengen verwendet werden.

2. Logistische Regression

Die logistische Regression ist eine der Arten von Regressionsanalysetechniken, die verwendet wird, wenn die abhängige Variable diskret ist. Beispiel: 0 oder 1, wahr oder falsch usw. Das bedeutet, dass die Zielvariable nur zwei Werte haben kann und eine Sigmoidkurve den Zusammenhang zwischen der Zielvariablen und der unabhängigen Variablen bezeichnet.

Die Logit-Funktion wird in der logistischen Regression verwendet, um die Beziehung zwischen der Zielvariablen und unabhängigen Variablen zu messen. Unten ist die Gleichung, die die logistische Regression bezeichnet.

logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3….+bkXk

wobei p die Wahrscheinlichkeit des Auftretens des Merkmals ist.

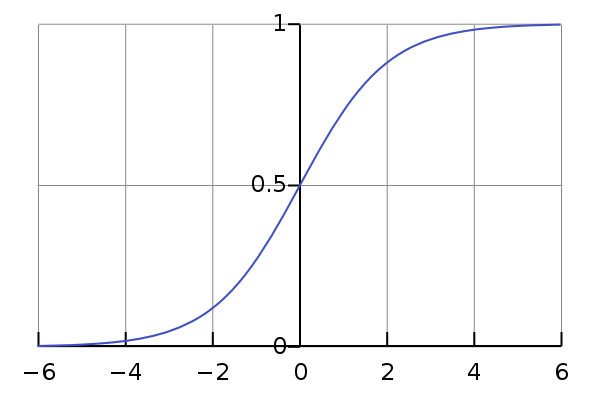
Quelle

Bei der Auswahl der logistischen Regression als Regressionsanalytiker-Technik sollte beachtet werden, dass die Datenmenge groß ist, mit dem fast gleichen Auftreten von Werten in Zielvariablen. Außerdem sollte es keine Multikollinearität geben, was bedeutet, dass es keine Korrelation zwischen unabhängigen Variablen im Datensatz geben sollte.

3. Ridge-Regression

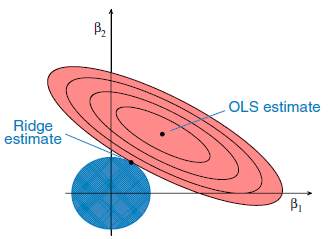
Quelle

Dies ist eine weitere Art der Regression beim maschinellen Lernen , die normalerweise verwendet wird, wenn eine hohe Korrelation zwischen den unabhängigen Variablen besteht. Dies liegt daran, dass bei multikollinearen Daten die Schätzungen der kleinsten Quadrate unverzerrte Werte liefern. Falls die Kollinearität jedoch sehr hoch ist, kann es zu einem gewissen Bias-Wert kommen. Daher wird eine Bias-Matrix in die Gleichung der Ridge-Regression eingeführt. Dies ist eine leistungsstarke Regressionsmethode, bei der das Modell weniger anfällig für Überanpassung ist.

Unten ist die Gleichung, die verwendet wird, um die Ridge-Regression zu bezeichnen, wobei die Einführung von λ (Lambda) das Problem der Multikollinearität löst:

β = (X^{T}X + λ*I)^{-1}X^{T}y

Schauen Sie sich an: 5 bahnbrechende Anwendungen des maschinellen Lernens

4. Lasso-Regression

Die Lasso-Regression ist eine der Regressionsarten beim maschinellen Lernen , die eine Regularisierung zusammen mit der Merkmalsauswahl durchführt. Es verbietet die absolute Größe des Regressionskoeffizienten. Dadurch nähert sich der Koeffizientenwert Null an, was bei der Ridge-Regression nicht der Fall ist.

Aus diesem Grund wird die Merkmalsauswahl in der Lasso-Regression verwendet, die es ermöglicht, einen Satz von Merkmalen aus dem Datensatz auszuwählen, um das Modell zu erstellen. Bei der Lasso-Regression werden nur die erforderlichen Merkmale verwendet und die anderen auf Null gesetzt. Dies hilft bei der Vermeidung der Überanpassung im Modell. Falls die unabhängigen Variablen stark kollinear sind, wählt die Lasso-Regression nur eine Variable aus und lässt andere Variablen auf Null schrumpfen.

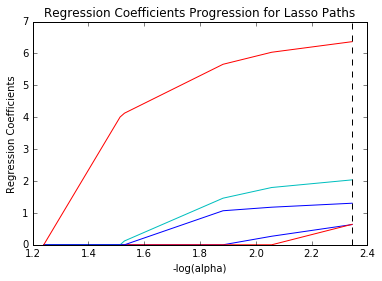
Quelle

Unten ist die Gleichung, die die Lasso-Regressionsmethode darstellt:

N^{-1}Σ^{N}_{i=1}f(x_{i}, y_{I}, α, β)

5. Polynomische Regression

Die polynomiale Regression ist eine weitere Art von Regressionsanalysetechniken beim maschinellen Lernen, die mit einer kleinen Modifikation der multiplen linearen Regression entspricht. Bei der polynomialen Regression wird die Beziehung zwischen unabhängigen und abhängigen Variablen, also X und Y, mit dem n-ten Grad bezeichnet.

Es ist ein lineares Modell als Schätzer. Die Least-Mean-Squared-Methode wird auch in der polynomialen Regression verwendet. Die am besten passende Linie in der polynomialen Regression, die durch alle Datenpunkte verläuft, ist keine gerade Linie, sondern eine gekrümmte Linie, die von der Potenz von X oder dem Wert von n abhängt.

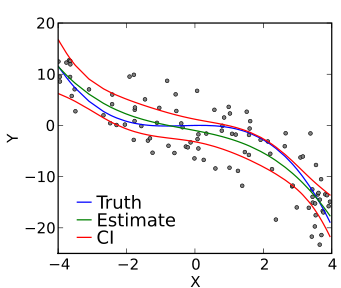
Quelle

Bei dem Versuch, den mittleren quadratischen Fehler auf ein Minimum zu reduzieren und die beste Anpassungslinie zu erhalten, kann das Modell anfällig für Überanpassung sein. Es wird empfohlen, die Kurve gegen Ende zu analysieren, da die höheren Polynome bei der Extrapolation seltsame Ergebnisse liefern können.

Die folgende Gleichung stellt die polynomiale Regression dar:

l = β0+ β0x1+ε

Lesen Sie: Projektideen für maschinelles Lernen

6. Bayessche lineare Regression

Bayes'sche Regression ist eine der Regressionsarten beim maschinellen Lernen , die das Bayes-Theorem verwendet, um den Wert von Regressionskoeffizienten zu ermitteln. Bei dieser Regressionsmethode wird die spätere Verteilung der Merkmale bestimmt, anstatt die kleinsten Quadrate zu finden. Die Bayes'sche lineare Regression ist wie die lineare Regression und die Ridge-Regression, aber stabiler als die einfache lineare Regression.

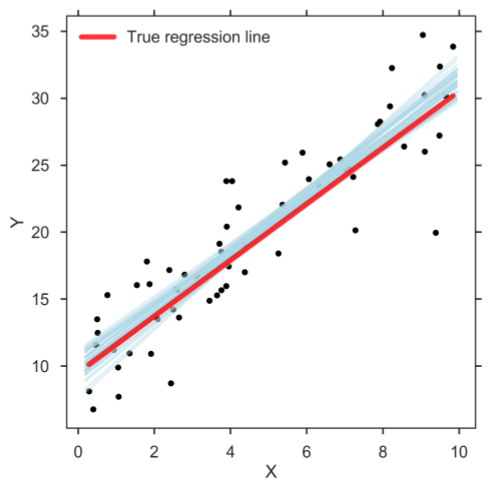
Quelle

Lernen Sie KI- und ML-Kurse online von den besten Universitäten der Welt – Masters, Executive Post Graduate Programs und Advanced Certificate Program in ML & KI, um Ihre Karriere zu beschleunigen.

Fazit

Zusätzlich zu den oben genannten Regressionsmethoden gibt es viele andere Arten der Regression beim maschinellen Lernen , einschließlich Elastic Net Regression, JackKnife Regression, Stepwise Regression und Ecological Regression.

Diese verschiedenen Arten von Regressionsanalysetechniken können zum Erstellen des Modells verwendet werden, abhängig von der Art der verfügbaren Daten oder derjenigen, die die maximale Genauigkeit bietet. Auf unserer Website können Sie diese Techniken genauer untersuchen oder den Kurs des überwachten Lernens durchlaufen .

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das Executive PG-Programm von IIIT-B & upGrad für maschinelles Lernen und KI an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben, IIIT, bietet -B Alumni-Status, mehr als 5 praktische Schlusssteinprojekte und Arbeitsunterstützung bei Top-Unternehmen.