知っておくべき機械学習の6種類の回帰モデル

序章

線形回帰とロジスティック回帰は、機械学習を使用して回帰問題を解決するために使用される2種類の回帰分析手法です。 それらは回帰の最も顕著な技術です。 ただし、機械学習には多くの種類の回帰分析手法があり、それらの使用法は関連するデータの性質によって異なります。

この記事では、機械学習におけるさまざまなタイプの回帰と、それぞれを使用できる条件について説明します。 機械学習を初めて使用する場合、この記事は回帰モデリングの概念を理解するのに役立ちます。

回帰分析とは何ですか？

回帰分析は、データセット内のターゲット変数または従属変数と独立変数の間の関係を分析する予測モデリング手法です。 ターゲット変数と独立変数が互いに線形または非線形の関係を示し、ターゲット変数に連続値が含まれている場合は、さまざまなタイプの回帰分析手法が使用されます。 回帰手法は、主に予測子の強度、予測の傾向、時系列を決定するために使用され、原因と結果の関係の場合に使用されます。

回帰分析は、データモデリングを使用して機械学習の回帰問題を解決するための主要な手法です。 これには、各データポイントからのラインの距離が最小になるように、すべてのデータポイントを通過するラインである最適なラインを決定することが含まれます。

回帰分析手法の種類

回帰分析の手法には多くの種類があり、それぞれの方法の使用は要因の数によって異なります。 これらの要因には、ターゲット変数のタイプ、回帰直線の形状、および独立変数の数が含まれます。

以下は、さまざまな回帰手法です。

1. 線形回帰
2. ロジスティック回帰
3. リッジ回帰
4. ラッソ回帰
5. 多項式回帰
6. ベイズ線形回帰

機械学習手法におけるさまざまなタイプの回帰について、以下で詳しく説明します。

1.線形回帰

線形回帰は、機械学習における最も基本的なタイプの回帰の1つです。 線形回帰モデルは、相互に線形に関連する予測変数と従属変数で構成されます。 データに複数の独立変数が含まれる場合、線形回帰は重回帰モデルと呼ばれます。

以下の方程式は、線形回帰モデルを表すために使用されます。

y = mx + c + e

ここで、mは直線の傾き、cは切片、eはモデルの誤差を表します。

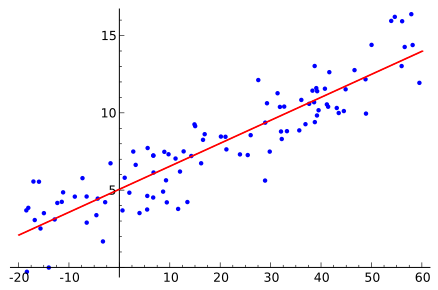
ソース

最適な線は、mとcの値を変えることによって決定されます。 予測誤差は、観測値と予測値の差です。 mとcの値は、予測誤差が最小になるように選択されます。 単純な線形回帰モデルは外れ値の影響を受けやすいことに注意することが重要です。 したがって、大きなサイズのデータ​​の場合は使用しないでください。

2.ロジスティック回帰

ロジスティック回帰は、従属変数が離散的である場合に使用される回帰分析手法の一種です。 例：0または1、trueまたはfalseなど。これは、ターゲット変数が持つことができる値が2つだけであることを意味し、シグモイド曲線はターゲット変数と独立変数の間の関係を示します。

ロジット関数は、ロジスティック回帰で使用され、ターゲット変数と独立変数の間の関係を測定します。 以下は、ロジスティック回帰を表す方程式です。

logit（p）= ln（p /（1-p））= b0 + b1X1 + b2X2+b3X3…。+bkXk

ここで、pは特徴の発生確率です。

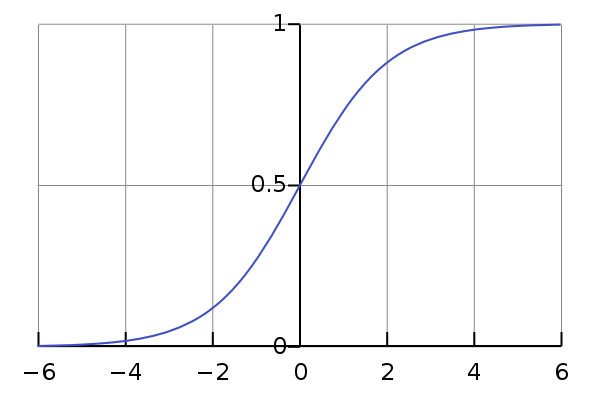
ソース

ロジスティック回帰を選択する場合、回帰アナリストの手法として、データのサイズが大きく、ターゲット変数に含まれる値がほぼ同じになることに注意してください。 また、多重共線性があってはなりません。つまり、データセット内の独立変数間に相関関係があってはなりません。

3.リッジ回帰

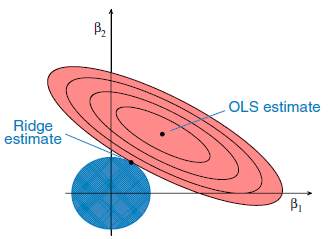
ソース

これは、機械学習の回帰のもう1つのタイプであり、独立変数間に高い相関関係がある場合に通常使用されます。 これは、複数の共線データの場合、最小二乗推定が偏りのない値を与えるためです。 ただし、共線性が非常に高い場合は、バイアス値が存在する可能性があります。 したがって、バイアス行列はリッジ回帰の方程式に導入されます。 これは、モデルが過剰適合の影響を受けにくい強力な回帰法です。

以下は、リッジ回帰を表すために使用される方程式です。ここで、λ（ラムダ）の導入により、多重共線性の問題が解決されます。

β=（X ^ {T} X+λ*I）^ {-1} X ^ {T} y

チェックアウト：機械学習の5つの画期的なアプリケーション

4.ラッソ回帰

ラッソ回帰は、特徴選択とともに正則化を実行する機械学習の回帰のタイプの1つです。 回帰係数の絶対サイズを禁止します。 その結果、係数値はゼロに近づきます。これは、リッジ回帰の場合には発生しません。

このため、特徴選択はLasso Regressionで使用され、データセットから特徴のセットを選択してモデルを構築できます。 ラッソ回帰の場合、必要な機能のみが使用され、他の機能はゼロになります。 これは、モデルの過剰適合を回避するのに役立ちます。 独立変数が高度に共線的である場合、ラッソ回帰は1つの変数のみを選択し、他の変数をゼロに縮小します。

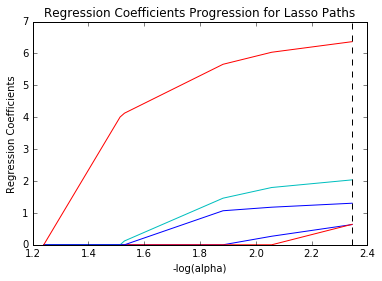
ソース

以下は、ラッソ回帰法を表す方程式です。

N^{-1}Σ^{N}_ {i = 1} f（x_ {i}、y_ {I}、α、β）

5.多項式回帰

多項式回帰は、機械学習における回帰分析手法のもう1つのタイプであり、少し変更を加えた重回帰と同じです。 多項式回帰では、独立変数と従属変数の関係、つまりXとYは、n次で表されます。

推定量としての線形モデルです。 最小平均二乗法は、多項式回帰でも使用されます。 すべてのデータポイントを通過する多項式回帰の最適な線は、直線ではなく、Xの累乗またはnの値に依存する曲線です。

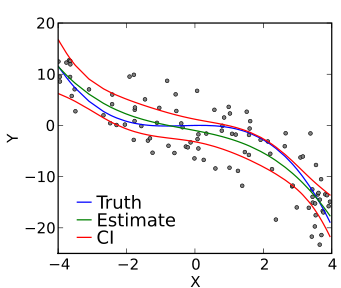
ソース

平均二乗誤差を最小限に抑え、最適な線を取得しようとすると、モデルが過剰適合しやすくなります。 より高い多項式は外挿で奇妙な結果をもたらす可能性があるため、曲線を最後に向かって分析することをお勧めします。

以下の方程式は、多項式回帰を表しています。

l=β0+β0x1+ε

読む：機械学習プロジェクトのアイデア

6.ベイズ線形回帰

ベイズ回帰は、ベイズの定理を使用して回帰係数の値を見つける機械学習の回帰のタイプの1つです。 この回帰方法では、最小二乗を見つける代わりに、特徴の事後分布が決定されます。 ベイジアン線形回帰は、線形回帰とリッジ回帰の両方に似ていますが、単純な線形回帰よりも安定しています。

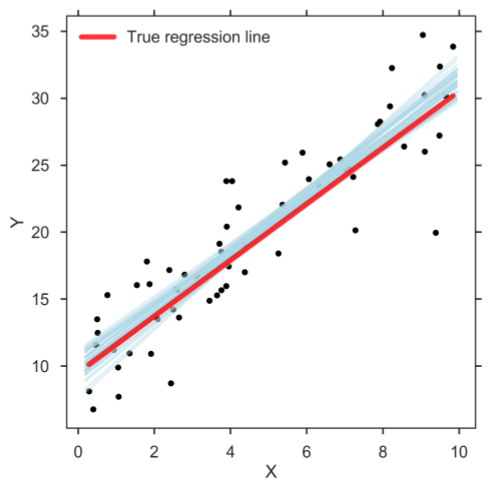
ソース

世界のトップ大学（修士、エグゼクティブ大学院プログラム、ML＆AIの高度な証明書プログラム）からオンラインでAI＆MLコースを学び、キャリアを早急に進めましょう。

結論

上記の回帰方法に加えて、機械学習には、エラスティックネット回帰、ジャックナイフ回帰、ステップワイズ回帰、エコロジカル回帰など、他の多くのタイプの回帰があります。

これらのさまざまなタイプの回帰分析手法を使用して、使用可能なデータの種類または最大の精度を提供するデータに応じてモデルを構築できます。 これらのテクニックをさらに詳しく調べたり、当社のWebサイトで教師あり学習のコースを受講したりできます。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。このプログラムは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIITを提供しています。 -B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との雇用支援。