您应该了解的机器学习中的 6 种回归模型

介绍

线性回归和逻辑回归是两种类型的回归分析技术，用于使用机器学习解决回归问题。 它们是最突出的回归技术。 但是，机器学习中有许多类型的回归分析技术，它们的使用根据所涉及数据的性质而有所不同。

本文将解释机器学习中不同类型的回归，以及在什么条件下可以使用它们。 如果你是机器学习的新手，这篇文章肯定会帮助你理解回归建模的概念。

什么是回归分析？

回归分析是一种预测建模技术，用于分析数据集中目标或因变量与自变量之间的关系。 当目标变量和自变量之间显示出线性或非线性关系，并且目标变量包含连续值时，就会使用不同类型的回归分析技术。 回归技术主要用于确定预测变量的强度、预测趋势、时间序列以及因果关系。

回归分析是使用数据建模解决机器学习中回归问题的主要技术。 它涉及确定最佳拟合线，这是一条穿过所有数据点的线，使得线与每个数据点的距离最小化。

回归分析技术的类型

回归分析技术有很多种，每种方法的使用取决于因素的数量。 这些因素包括目标变量的类型、回归线的形状和自变量的数量。

以下是不同的回归技术：

1. 线性回归
2. 逻辑回归
3. 岭回归
4. 套索回归
5. 多项式回归
6. 贝叶斯线性回归

下面详细解释机器学习技术中不同类型的回归：

1. 线性回归

线性回归是机器学习中最基本的回归类型之一。 线性回归模型由相互线性相关的预测变量和因变量组成。 如果数据涉及多个自变量，则线性回归称为多元线性回归模型。

下面给出的方程用于表示线性回归模型：

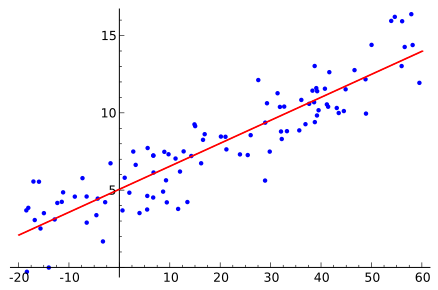
y=mx+c+e

其中 m 是直线的斜率，c 是截距，e 表示模型中的误差。

资源

最佳拟合线是通过改变 m 和 c 的值来确定的。 预测误差是观测值与预测值之间的差值。 m 和 c 的值以给出最小预测误差的方式选择。 需要注意的是，简单的线性回归模型容易受到异常值的影响。 因此，不应在大数据的情况下使用它。

2. 逻辑回归

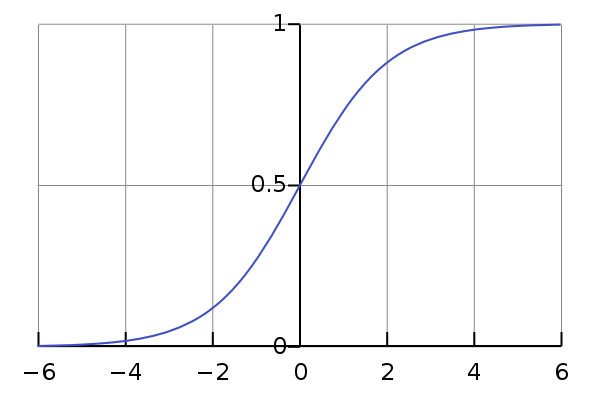
逻辑回归是回归分析技术的一种，当因变量是离散的时使用。 示例：0 或 1，真或假等。这意味着目标变量只能有两个值，而 sigmoid 曲线表示目标变量和自变量之间的关系。

Logit 函数在 Logistic 回归中用于衡量目标变量与自变量之间的关系。 下面是表示逻辑回归的方程。

logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3….+bkXk

其中 p 是特征出现的概率。

资源

对于选择逻辑回归，作为回归分析技术，应该注意，数据量很大，目标变量中出现的值几乎相等。 此外，不应存在多重共线性，这意味着数据集中的自变量之间不应存在相关性。

3. 岭回归

资源

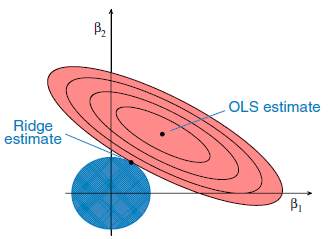
这是机器学习中的另一种回归类型，通常在自变量之间存在高度相关性时使用。 这是因为，在多共线数据的情况下，最小二乘估计会给出无偏值。 但是，如果共线性非常高，可能会有一些偏差值。 因此，在岭回归方程中引入了一个偏置矩阵。 这是一种强大的回归方法，模型不易过度拟合。

下面是用于表示岭回归的方程，其中引入 λ (lambda) 解决了多重共线性问题：

β = (X^{T}X + λ*I)^{-1}X^{T}y

查看：机器学习的 5 个突破性应用

4. 套索回归

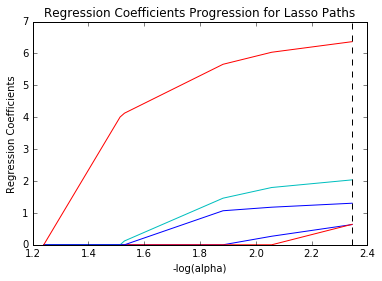
套索回归是机器学习中的一种回归类型，它与特征选择一起执行正则化。 它禁止回归系数的绝对大小。 结果，系数值接近于零，这在岭回归的情况下不会发生。

因此，Lasso Regression 中使用了特征选择，它允许从数据集中选择一组特征来构建模型。 在 Lasso Regression 的情况下，仅使用所需的特征，而其他特征为零。 这有助于避免模型中的过度拟合。 如果自变量高度共线，那么 Lasso 回归只选择一个变量，并使其他变量缩小到零。

资源

下面是代表 Lasso 回归方法的方程：

N^{-1}Σ^{N}_{i=1}f(x_{i}, y_{I}, α, β)

5. 多项式回归

多项式回归是机器学习中的另一种回归分析技术，它与多元线性回归相同，只是稍作修改。 在多项式回归中，自变量和因变量之间的关系，即 X 和 Y，用 n 次表示。

它是作为估计量的线性模型。 最小均方法也用于多项式回归。 多项式回归中穿过所有数据点的最佳拟合线不是直线，而是曲线，这取决于 X 的幂或 n 的值。

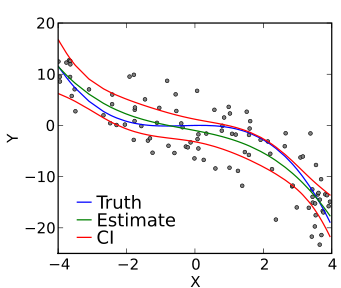
资源

在尝试将均方误差降至最低并获得最佳拟合线时，该模型可能容易过度拟合。 建议对曲线进行分析，因为较高的多项式可能会在外推时给出奇怪的结果。

下面的等式代表多项式回归：

l = β0+ β0x1+ε

阅读：机器学习项目理念

6.贝叶斯线性回归

贝叶斯回归是机器学习中的一种回归类型，它使用贝叶斯定理找出回归系数的值。 在这种回归方法中，确定特征的后验分布而不是寻找最小二乘。 贝叶斯线性回归类似于线性回归和岭回归，但比简单的线性回归更稳定。

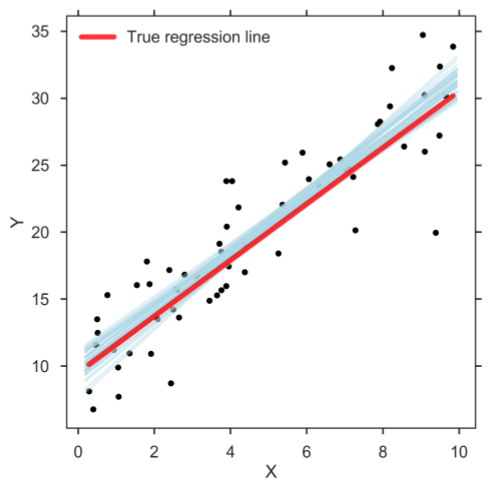
资源

从世界顶级大学在线学习AI 和 ML 课程- 硕士、高级管理人员研究生课程和 ML 和 AI 高级证书课程，以加快您的职业生涯。

结论

除了上述回归方法外，机器学习中还有很多其他类型的回归，包括弹性网络回归、JackKnife 回归、逐步回归和生态回归。

这些不同类型的回归分析技术可用于构建模型，具体取决于可用数据的类型或提供最大准确度的数据。 您可以更多地探索这些技术，也可以通过我们网站上的监督学习课程进行学习。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和 AI 执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT -B 校友身份，5 个以上实用的实践顶点项目和顶级公司的工作协助。