Makine Öğreniminde Bilmeniz Gereken 6 Tip Regresyon Modeli

Tanıtım

Doğrusal regresyon ve lojistik regresyon, makine öğrenimi kullanarak regresyon problemini çözmek için kullanılan iki tür regresyon analizi tekniğidir. Bunlar en belirgin regresyon teknikleridir. Ancak, makine öğreniminde birçok türde regresyon analizi tekniği vardır ve bunların kullanımı, ilgili verilerin doğasına göre değişir.

Bu makale, makine öğrenimindeki farklı regresyon türlerini ve her birinin hangi koşullar altında kullanılabileceğini açıklayacaktır. Makine öğreniminde yeniyseniz, bu makale kesinlikle regresyon modelleme kavramını anlamanıza yardımcı olacaktır.

Regresyon Analizi Nedir?

Regresyon analizi, bir veri setindeki hedef veya bağımlı değişken ile bağımsız değişken arasındaki ilişkiyi analiz eden tahmine dayalı bir modelleme tekniğidir. Hedef ve bağımsız değişkenler birbirleri arasında doğrusal veya doğrusal olmayan bir ilişki gösterdiğinde ve hedef değişken sürekli değerler içerdiğinde farklı tipte regresyon analizi teknikleri kullanılır. Regresyon tekniği esas olarak tahmin gücünü, tahmin eğilimini, zaman serisini ve neden-sonuç ilişkisi durumunda belirlemek için kullanılır.

Regresyon analizi, veri modelleme kullanarak makine öğrenimindeki regresyon problemlerini çözmek için birincil tekniktir. Tüm veri noktalarından geçen ve çizginin her bir veri noktasından uzaklığı en aza indirilecek şekilde geçen bir çizgi olan en uygun çizginin belirlenmesini içerir.

Regresyon Analizi Tekniklerinin Türleri

Birçok türde regresyon analizi tekniği vardır ve her yöntemin kullanımı faktör sayısına bağlıdır. Bu faktörler, hedef değişkenin tipini, regresyon çizgisinin şeklini ve bağımsız değişkenlerin sayısını içerir.

Aşağıda farklı regresyon teknikleri verilmiştir:

1. Doğrusal Regresyon
2. Lojistik regresyon
3. Sırt Regresyonu
4. Kement Regresyonu
5. Polinom Regresyon
6. Bayes Doğrusal Regresyon

Makine öğrenimi tekniklerindeki farklı regresyon türleri aşağıda ayrıntılı olarak açıklanmıştır:

1. Doğrusal Regresyon

Doğrusal regresyon, makine öğrenimindeki en temel regresyon türlerinden biridir . Doğrusal regresyon modeli, birbiriyle doğrusal olarak ilişkili bir yordayıcı değişken ve bir bağımlı değişkenden oluşur. Verinin birden fazla bağımsız değişken içermesi durumunda, doğrusal regresyon, çoklu doğrusal regresyon modelleri olarak adlandırılır.

Aşağıda verilen denklem, doğrusal regresyon modelini belirtmek için kullanılır:

y=mx+c+e

burada m doğrunun eğimidir, c bir kesme noktasıdır ve e modeldeki hatayı temsil eder.

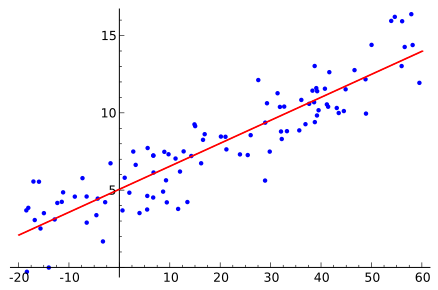
Kaynak

En uygun çizgi, m ve c değerleri değiştirilerek belirlenir. Tahmin hatası, gözlenen değerler ile tahmin edilen değer arasındaki farktır. m ve c değerleri minimum tahmin hatası verecek şekilde seçilir. Basit bir doğrusal regresyon modelinin aykırı değerlere duyarlı olduğunu belirtmek önemlidir. Bu nedenle büyük veri olması durumunda kullanılmamalıdır.

2. Lojistik Regresyon

Lojistik regresyon, bağımlı değişken kesikli olduğunda kullanılan regresyon analizi tekniklerinden biridir. Örnek: 0 veya 1, doğru veya yanlış, vb. Bu, hedef değişkenin yalnızca iki değere sahip olabileceği anlamına gelir ve bir sigmoid eğri, hedef değişken ile bağımsız değişken arasındaki ilişkiyi belirtir.

Logit fonksiyonu, Lojistik Regresyonda hedef değişken ile bağımsız değişkenler arasındaki ilişkiyi ölçmek için kullanılır. Lojistik regresyonu gösteren denklem aşağıdadır.

logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3….+bkXk

p, özelliğin ortaya çıkma olasılığıdır.

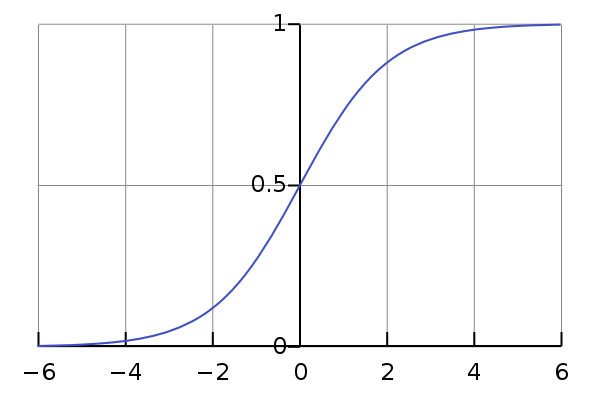
Kaynak

Lojistik regresyonu seçmek için, regresyon analisti tekniği olarak, not edilmelidir, hedef değişkenlerde gelecek değerlerin neredeyse eşit oluşumu ile veri boyutu büyüktür. Ayrıca veri setindeki bağımsız değişkenler arasında herhangi bir korelasyon olmaması gerektiği anlamına gelen çoklu bağlantı olmamalıdır.

3. Sırt Regresyonu

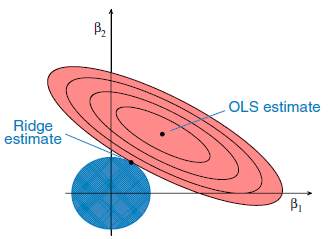
Kaynak

Bu, genellikle bağımsız değişkenler arasında yüksek bir korelasyon olduğunda kullanılan, makine öğrenimindeki regresyon türlerinden bir diğeridir . Bunun nedeni, çoklu doğrusal veri durumunda, en küçük kareler tahminlerinin yansız değerler vermesidir. Ancak, doğrusallığın çok yüksek olması durumunda, bir miktar yanlılık değeri olabilir. Bu nedenle, Ridge Regresyon denklemine bir yanlılık matrisi eklenmiştir. Bu, modelin fazla uydurmaya daha az duyarlı olduğu güçlü bir regresyon yöntemidir.

Aşağıda, λ'nın (lambda) tanıtılmasının çoklu doğrusallık problemini çözdüğü Ridge Regresyonunu belirtmek için kullanılan denklem verilmiştir:

β = (X^{T}X + λ*I)^{-1}X^{T}y

Kontrol edin: Makine Öğreniminin 5 Çığır Açan Uygulaması

4. Kement Regresyonu

Kement Regresyon, özellik seçimi ile birlikte düzenlileştirme gerçekleştiren makine öğrenimindeki regresyon türlerinden biridir . Regresyon katsayısının mutlak boyutunu yasaklar. Sonuç olarak, katsayı değeri sıfıra yaklaşır, bu Ridge Regresyon durumunda olmaz.

Bu nedenle, model oluşturmak için veri kümesinden bir dizi özellik seçilmesine izin veren Kement Regresyonunda özellik seçimi kullanılır. Kement Regresyon durumunda sadece gerekli özellikler kullanılır ve diğerleri sıfırlanır. Bu, modeldeki fazla takmadan kaçınmaya yardımcı olur. Bağımsız değişkenlerin yüksek oranda eşdoğrusal olması durumunda, Kement regresyonu yalnızca bir değişken seçer ve diğer değişkenlerin sıfıra küçülmesini sağlar.

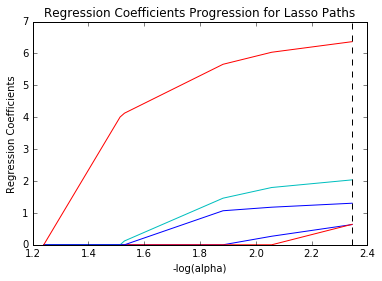
Kaynak

Kement Regresyon yöntemini temsil eden denklem aşağıdadır:

N^{-1}Σ^{N}_{i=1}f(x_{i}, y_{I}, α, β)

5. Polinom Regresyon

Polinom Regresyon, küçük bir değişiklikle Çoklu Doğrusal Regresyon ile aynı olan, makine öğrenimindeki regresyon analizi tekniklerinden bir diğeridir . Polinom Regresyonda bağımsız ve bağımlı değişkenler, yani X ve Y arasındaki ilişki n'inci derece ile gösterilir.

Tahmin edici olarak doğrusal bir modeldir. En Küçük Ortalama Kareler Yöntemi, Polinom Regresyonda da kullanılmaktadır. Polinom Regresyonda tüm veri noktalarından geçen en uygun çizgi, düz bir çizgi değil, X'in gücüne veya n'nin değerine bağlı olan eğri bir çizgidir.

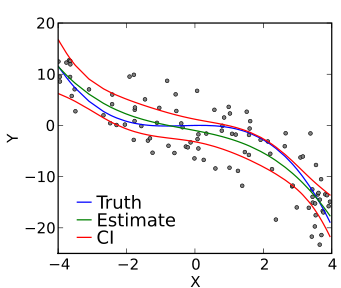
Kaynak

Ortalama Kare Hatasını en aza indirmeye ve en iyi uyum çizgisini elde etmeye çalışırken, model fazla uydurmaya meyilli olabilir. Daha yüksek Polinomlar ekstrapolasyonda garip sonuçlar verebileceğinden, eğrinin sona doğru analiz edilmesi önerilir.

Aşağıdaki denklem Polinom Regresyonunu temsil eder:

l = β0+ β0x1+ε

Okuyun: Makine Öğrenimi Proje Fikirleri

6. Bayes Doğrusal Regresyon

Bayesian Regresyon, regresyon katsayılarının değerini bulmak için Bayes teoremini kullanan makine öğrenimindeki regresyon türlerinden biridir . Bu regresyon yönteminde, en küçük kareleri bulmak yerine özniteliklerin sonsal dağılımı belirlenir. Bayesian Lineer Regresyon, hem Lineer Regresyon hem de Ridge Regresyon gibidir, ancak basit Lineer Regresyondan daha kararlıdır.

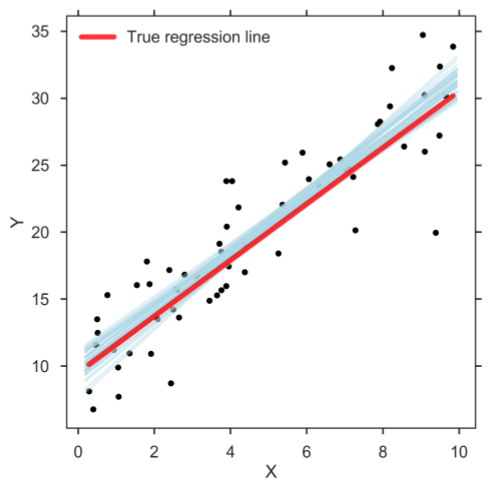
Kaynak

Kariyerinizi hızlandırmak için Dünyanın en iyi Üniversiteleri - Yüksek Lisanslar, Yönetici Yüksek Lisans Programları ve Makine Öğrenimi ve Yapay Zekada İleri Düzey Sertifika Programından çevrimiçi olarak AI ve ML Kursları öğrenin.

Çözüm

Yukarıdaki regresyon yöntemlerine ek olarak, Elastic Net Regresyon, JackKnife Regresyon, Kademeli Regresyon ve Ekolojik Regresyon dahil olmak üzere makine öğreniminde birçok başka regresyon türü vardır.

Bu farklı tipteki regresyon analizi teknikleri, mevcut veri türüne veya maksimum doğruluğu verene bağlı olarak modeli oluşturmak için kullanılabilir. Bu teknikleri daha fazla keşfedebilir veya web sitemizde denetimli öğrenme kursunu inceleyebilirsiniz .

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka alanında Yönetici PG Programına göz atın. -B Mezunu statüsü, 5'ten fazla pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.