邏輯回歸中的梯度下降[為初學者解釋]

在本文中，我們將討論邏輯回歸中非常流行的梯度下降算法。 我們將研究什麼是邏輯回歸，然後逐漸轉向邏輯回歸方程、成本函數，最後是梯度下降算法。

什麼是邏輯回歸？

邏輯回歸只是一種用於預測離散類別的分類算法，例如預測郵件是“垃圾郵件”還是“非垃圾郵件”； 預測給定數字是“9”還是“非 9”等。現在，通過查看名稱，您一定會想，為什麼將其命名為 Regression？

原因是，邏輯回歸的想法是通過調整回歸問題中使用的基本線性回歸算法的一些元素而發展起來的。

邏輯回歸也可以應用於多類（多於兩個類）分類問題。 雖然，建議僅將此算法用於二元分類問題。

Sigmoid 函數

分類問題不是線性函數問題。 輸出僅限於某些離散值，例如二進制分類問題的 0 和 1。 線性函數預測我們的輸出值大於 1 或小於 0 是沒有意義的。所以我們需要一個合適的函數來表示我們的輸出值。

Sigmoid 函數解決了我們的問題。 也稱為 Logistic 函數，它是一個 S 形函數，將任何實數值數映射到 (0,1) 區間，因此在將任何隨機函數轉換為基於分類的函數時非常有用。 Sigmoid 函數如下所示：

Sigmoid 函數

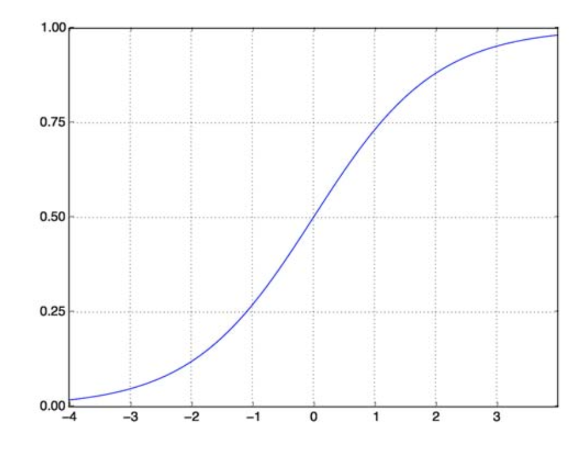
資源

現在參數化向量和輸入向量 X 的 sigmoid 函數的數學形式為：

(z) = 11+exp(-z) 其中 z = TX

(z) 將給我們輸出為 1 的概率。眾所周知，概率值的範圍從 0 到 1。現在，這不是我們想要的基於離散（僅 0 和 1）分類問題的輸出. 所以現在我們可以將預測概率與 0.5 進行比較。 如果概率 > 0.5，我們有 y=1。 類似地，如果概率 < 0.5，我們有 y=0。

成本函數

現在我們有了離散預測，是時候檢查我們的預測是否確實正確。 為此，我們有一個成本函數。 成本函數僅僅是整個數據集的預測中所有錯誤的總和。 當然，我們不能使用線性回歸中使用的成本函數。 所以邏輯回歸的新成本函數是：

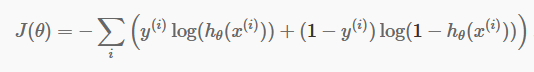資源

不要害怕等式。 這很簡單。 對於每次迭代i ，它都會計算我們在預測中產生的誤差，然後將所有誤差相加來定義我們的成本函數 J()。

括號內的兩項實際上是針對兩種情況：y=0 和 y=1。 當 y=0 時，第一項消失，我們只剩下第二項。 同樣，當 y=1 時，第二項消失，我們只剩下第一項。

梯度下降算法

我們已經成功計算了我們的成本函數。 但是我們需要最小化損失來做出一個好的預測算法。 為此，我們有梯度下降算法。

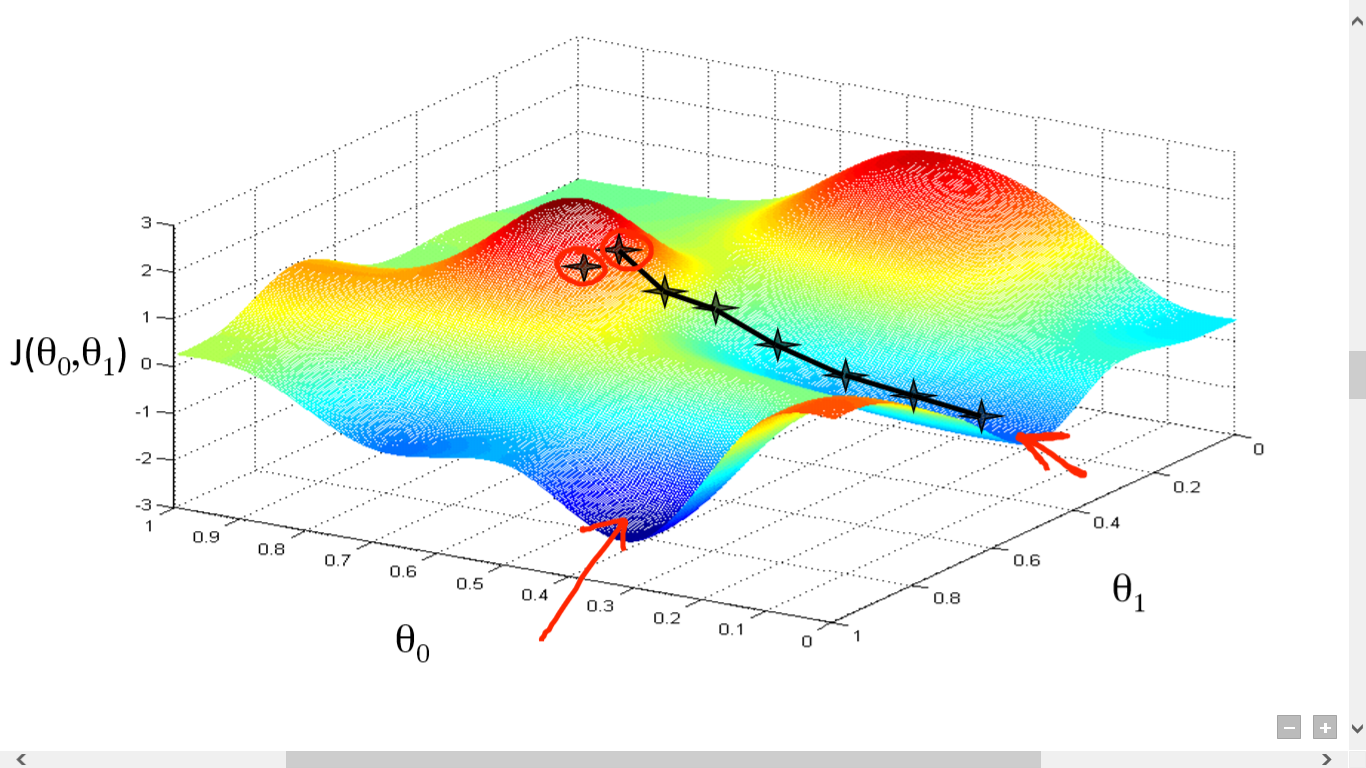資源

在這裡，我們在 J() 和 之間繪製了一個圖表。 我們的目標是找到這個函數的最深點（全局最小值）。 現在最深點是 J() 最小的地方。

找到最深點需要兩件事：

• 導數——尋找下一步的方向。
• （學習率）——下一步的幅度

這個想法是你首先從函數中選擇任何隨機點。 然後你需要計算 J()wrt 的導數。 這將指向局部最小值的方向。 現在將結果梯度與學習率相乘。 學習率沒有固定值，要根據問題來決定。

現在，您需要從中減去結果以獲得新的 .

這個更新應該同時為每個 (i) 完成。

重複執行這些步驟，直到達到局部或全局最小值。 通過達到全局最小值，您在預測中實現了盡可能低的損失。

取衍生品很簡單。 只要你在高中必須完成的基本微積分就足夠了。 主要問題在於學習率（）。 採用良好的學習率很重要，而且通常很困難。

如果您採用非常小的學習率，每一步都會太小，因此您將花費大量時間來達到局部最小值。

現在，如果你傾向於採用一個巨大的學習率值，你將超過最小值並且永遠不會再次收斂。 完美的學習率沒有特定的規則。

您需要對其進行調整以準備最佳模型。

梯度下降的方程是：

重複直到收斂：

所以我們可以將梯度下降算法總結為：

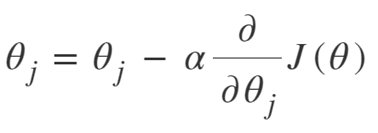
1. 從隨機開始
2. 循環直到收斂：
   1. 計算梯度
   2. 更新
3. 返回

隨機梯度下降算法

現在，梯度下降算法是最小化成本函數的一種很好的算法，特別是對於中小型數據。 但是當我們需要處理更大的數據集時，梯度下降算法的計算速度會很慢。 原因很簡單：它需要計算梯度，並同時更新每個參數的值，每個訓練樣本也是如此。

所以想想所有這些計算！ 它很大，因此需要稍微修改一下梯度下降算法，即——隨機梯度下降算法（SGD）。

SGD 與 Normal Gradient Descent 的唯一區別在於，在 SGD 中，我們不會一次處理整個訓練實例。 在 SGD 中，我們在每次迭代中僅計算單個隨機示例的成本函數的梯度。

現在，這樣做可以大大減少計算所需的時間，尤其是對於大型數據集。 SGD 採用的路徑非常隨意且嘈雜（儘管嘈雜的路徑可能使我們有機會達到全局最小值）。

但這沒關係，因為我們不必擔心所走的路。

我們只需要在更快的時間內達到最小的損失。

所以我們可以將梯度下降算法總結為：

1. 循環直到收斂：
   1. 選擇單個數據點“ i”
   2. 在該單點上計算梯度
   3. 更新
2. 返回

小批量梯度下降算法

Mini-Batch Gradient Descent 是對 Gradient Descent 算法的另一個輕微修改。 它介於正常梯度下降和隨機梯度下降之間。

Mini-Batch Gradient Descent 只是取整個數據集的一小部分，然後最小化它的損失。

這個過程比上述兩種梯度下降算法都更有效。 現在批量大小當然可以是你想要的任何東西。

但研究人員表明，最好將其保持在 1 到 100 之間，其中 32 是最佳批量大小。

因此，在大多數框架中，batch size = 32 保持默認。

1. 循環直到收斂：
   1. 選擇一批“ b ”個數據點
   2. 計算該批次的梯度
   3. 更新
2. 返回

結論

現在你對邏輯回歸有了理論上的理解。 您已經學習瞭如何以數學方式表示邏輯函數。 您知道如何使用成本函數來衡量預測誤差。

您還知道如何使用梯度下降算法將這種損失降至最低。

最後，您知道應該為您的問題選擇哪種梯度下降算法變體。 upGrad 提供機器學習和人工智能的PG 文憑和機器學習和人工智能的理學碩士，可以指導您建立職業生涯。 這些課程將解釋機器學習的必要性以及收集該領域知識的進一步步驟，涵蓋從梯度下降算法到神經網絡的各種概念。