Spadek gradientu w regresji logistycznej [wyjaśnienie dla początkujących]

W tym artykule omówimy bardzo popularny algorytm opadania gradientu w regresji logistycznej. Przyjrzymy się, czym jest regresja logistyczna, a następnie stopniowo przejdziemy do równania regresji logistycznej, jego funkcji kosztu i wreszcie algorytmu gradientu opadania.

Co to jest regresja logistyczna?

Regresja logistyczna to po prostu algorytm klasyfikacji używany do przewidywania odrębnych kategorii, takich jak przewidywanie, czy wiadomość jest „spamem”, czy „nie spamem”; przewidywanie, czy dana cyfra to „9” czy „nie 9” itd. Teraz, patrząc na nazwę, musisz pomyśleć, dlaczego nazywa się ona Regresja?

Powodem jest to, że idea regresji logistycznej została rozwinięta poprzez ulepszenie kilku elementów podstawowego algorytmu regresji liniowej używanego w problemach regresji.

Regresję logistyczną można również zastosować do problemów klasyfikacji wieloklasowej (więcej niż dwie klasy). Chociaż zaleca się używanie tego algorytmu tylko w przypadku problemów z klasyfikacją binarną.

Funkcja sigmoidalna

Problemy klasyfikacji nie są problemami funkcji liniowych. Wyjście jest ograniczone do pewnych wartości dyskretnych, np. 0 i 1 dla problemu klasyfikacji binarnej. Nie ma sensu, aby funkcja liniowa przewidywała nasze wartości wyjściowe jako większe niż 1 lub mniejsze niż 0. Potrzebujemy więc odpowiedniej funkcji do reprezentowania naszych wartości wyjściowych.

Funkcja sigmoidalna rozwiązuje nasz problem. Znana również jako funkcja logistyczna, jest to funkcja w kształcie litery S odwzorowująca dowolną liczbę wartości rzeczywistej na przedział (0,1), co czyni ją bardzo użyteczną w przekształcaniu dowolnej funkcji losowej w funkcję opartą na klasyfikacji. Funkcja sigmoidalna wygląda tak:

Funkcja sigmoidalna

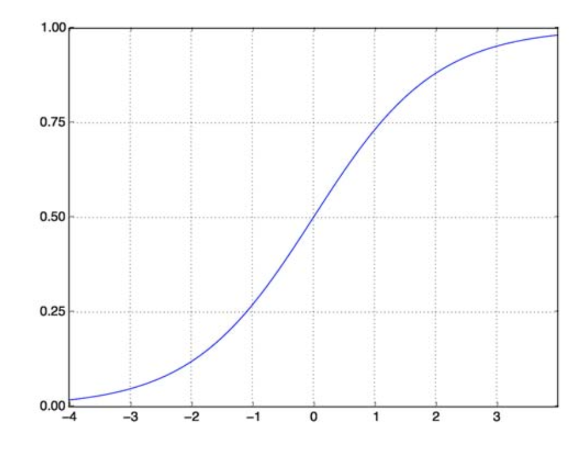
źródło

Teraz matematyczna postać funkcji sigmoidalnej dla sparametryzowanego wektora i wektora wejściowego X to:

(z) = 11+exp(-z) gdzie z = TX

(z) da nam prawdopodobieństwo, że wynik będzie równy 1. Jak wszyscy wiemy, wartość prawdopodobieństwa mieści się w zakresie od 0 do 1. To nie jest wynik, którego chcemy dla naszego problemu klasyfikacji opartej na dyskretnych (tylko 0 i 1) . Więc teraz możemy porównać przewidywane prawdopodobieństwo z 0,5. Jeśli prawdopodobieństwo > 0,5, mamy y=1. Podobnie, jeśli prawdopodobieństwo jest < 0,5, mamy y=0.

Funkcja kosztów

Teraz, gdy mamy już nasze dyskretne przewidywania, nadszedł czas, aby sprawdzić, czy nasze przewidywania są rzeczywiście poprawne, czy nie. Aby to zrobić, mamy funkcję kosztów. Funkcja kosztu jest jedynie sumą wszystkich błędów popełnionych w prognozach w całym zbiorze danych. Oczywiście nie możemy użyć funkcji kosztu używanej w regresji liniowej. Tak więc nowa funkcja kosztów dla regresji logistycznej to:

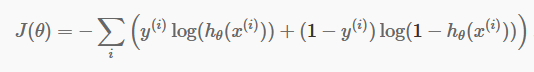źródło

Nie bój się równania. To bardzo proste. Dla każdej iteracji i oblicza się błąd, który popełniliśmy w naszej prognozie, a następnie sumuje wszystkie błędy, aby zdefiniować naszą funkcję kosztu J().

Dwa terminy w nawiasie odnoszą się w rzeczywistości do dwóch przypadków: y=0 i y=1. Kiedy y=0, pierwszy składnik znika i zostaje tylko drugi składnik. Podobnie, gdy y=1, drugi składnik znika i zostaje tylko pierwszy składnik.

Algorytm opadania gradientu

Pomyślnie obliczyliśmy naszą funkcję kosztów. Ale musimy zminimalizować straty, aby stworzyć dobry algorytm przewidywania. Aby to zrobić, mamy algorytm opadania gradientu.

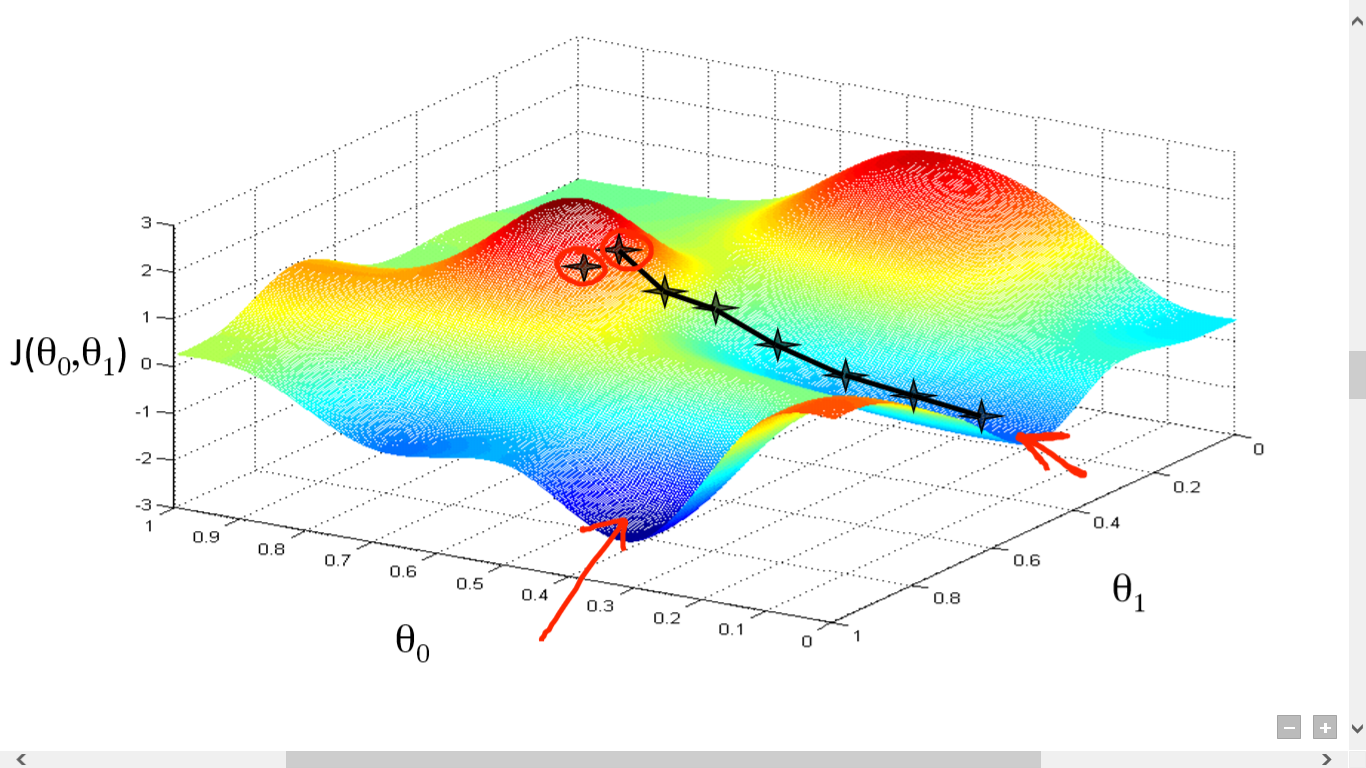źródło

Tutaj narysowaliśmy wykres między J() i . Naszym celem jest znalezienie najgłębszego punktu (globalnego minimum) tej funkcji. Teraz najgłębszym punktem jest miejsce, w którym J() jest minimum.

Aby znaleźć najgłębszy punkt, potrzebne są dwie rzeczy:

• Pochodna – aby znaleźć kierunek następnego kroku.
• (Learning Rate) – wielkość kolejnego kroku

Pomysł polega na tym, aby najpierw wybrać dowolny losowy punkt z funkcji. Następnie musisz obliczyć pochodną J()wrt . Wskaże to kierunek lokalnego minimum. Teraz pomnóż wynikowy gradient przez współczynnik uczenia się. Współczynnik uczenia się nie ma ustalonej wartości i należy go ustalać na podstawie problemów.

Teraz musisz odjąć wynik od, aby uzyskać nowy .

Ta aktualizacja powinna być wykonywana jednocześnie dla każdego (i) .

Wykonuj te kroki wielokrotnie, aż osiągniesz lokalne lub globalne minimum. Osiągając globalne minimum, osiągnąłeś najniższą możliwą stratę w swojej prognozie.

Przyjmowanie instrumentów pochodnych jest proste. Wystarczy podstawowy rachunek, który musiałeś zrobić w liceum. Główny problem dotyczy wskaźnika uczenia się ( ). Dobry wskaźnik uczenia się jest ważny i często trudny.

Jeśli przyjmiesz bardzo małą szybkość uczenia się, każdy krok będzie za mały, a co za tym idzie, dotarcie do lokalnego minimum zajmie Ci dużo czasu.

Teraz, jeśli masz tendencję do przyjmowania ogromnej wartości współczynnika uczenia się, przekroczysz minimum i nigdy więcej nie osiągniesz zbieżności. Nie ma określonej zasady idealnej szybkości uczenia się.

Musisz go podrasować, aby przygotować najlepszy model.

Równanie Gradient Descent to:

Powtarzaj aż do zbieżności:

Możemy więc podsumować algorytm opadania gradientu jako:

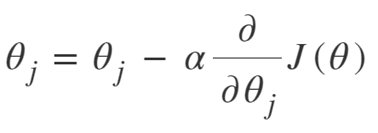
1. Zacznij od losowo
2. Pętla do zbieżności:
   1. Oblicz gradient
   2. Aktualizacja
3. Powrót

Stochastyczny algorytm opadania gradientu

Gradient Descent Algorithm to doskonały algorytm do minimalizowania funkcji kosztu, szczególnie w przypadku małych i średnich danych. Ale kiedy musimy poradzić sobie z większymi zestawami danych, algorytm gradientu opadania okazuje się powolny w obliczeniach. Powód jest prosty: musi obliczyć gradient i jednocześnie zaktualizować wartości dla każdego parametru, a także dla każdego przykładu treningowego.

Pomyśl więc o tych wszystkich obliczeniach! Jest ogromny, stąd potrzeba nieco zmodyfikowanego algorytmu gradientu gradientu, czyli Stochastic Gradient Descent Algorithm (SGD).

Jedyna różnica między SGD a Normal Gradient Descent polega na tym, że w SGD nie zajmujemy się całą instancją treningową na raz. W SGD obliczamy gradient funkcji kosztu tylko dla jednego losowego przykładu w każdej iteracji.

Teraz w ten sposób skraca się czas potrzebny na obliczenia o ogromny margines, zwłaszcza w przypadku dużych zestawów danych. Ścieżka obrana przez SGD jest bardzo chaotyczna i hałaśliwa (chociaż hałaśliwa ścieżka może dać nam szansę na osiągnięcie globalnych minimów).

Ale to jest w porządku, ponieważ nie musimy się martwić obraną ścieżką.

Musimy tylko szybciej osiągnąć minimalną stratę.

Możemy więc podsumować algorytm opadania gradientu jako:

1. Pętla do zbieżności:
   1. Wybierz pojedynczy punkt danych „ i”
   2. Oblicz gradient w tym pojedynczym punkcie
   3. Aktualizacja
2. Powrót

Algorytm opadania gradientu mini-partii

Mini-partia Gradient Descent to kolejna niewielka modyfikacja algorytmu Gradient Descent Algorithm. Znajduje się nieco pomiędzy normalnym spadkiem gradientu a stochastycznym spadkiem gradientu.

Mini-partia Gradient Descent po prostu pobiera mniejszą partię całego zestawu danych, a następnie minimalizuje na niej straty.

Ten proces jest bardziej wydajny niż oba powyższe algorytmy opadania gradientu. Teraz rozmiar partii może być oczywiście dowolny.

Ale naukowcy wykazali, że lepiej jest trzymać go w przedziale od 1 do 100, przy czym 32 to najlepsza wielkość partii.

W związku z tym rozmiar partii = 32 jest utrzymywany domyślnie w większości platform.

1. Pętla do zbieżności:
   1. Wybierz partię „ b ” punktów danych
   2. Oblicz gradient w tej partii
   3. Aktualizacja
2. Powrót

Wniosek

Teraz masz teoretyczne zrozumienie regresji logistycznej. Nauczyłeś się matematycznie przedstawiać funkcję logistyczną. Wiesz, jak zmierzyć przewidywany błąd za pomocą funkcji kosztu.

Wiesz również, w jaki sposób możesz zminimalizować tę stratę, korzystając z algorytmu Gradient Descent.

Na koniec wiesz, którą odmianę algorytmu gradientu opadania powinieneś wybrać dla swojego problemu. upGrad zapewnia dyplom PG w dziedzinie uczenia maszynowego i sztucznej inteligencji oraz tytuł magistra w dziedzinie uczenia maszynowego i sztucznej inteligencji , które mogą poprowadzić Cię w kierunku budowania kariery. Kursy te wyjaśnią potrzebę uczenia maszynowego i dalszych kroków w celu gromadzenia wiedzy w tej dziedzinie, obejmującej różne koncepcje, od algorytmów gradientu po sieci neuronowe.