Gradient Descent ในการถดถอยโลจิสติก [อธิบายสำหรับผู้เริ่มต้น]

ในบทความนี้ เราจะพูดถึงอัลกอริทึม Gradient Descent ที่ได้รับความนิยมอย่างมากในการถดถอยโลจิสติก เราจะพิจารณาว่า Logistic Regression คืออะไร จากนั้นค่อยๆ ย้ายไปยังสมการสำหรับการถดถอยโลจิสติก ฟังก์ชันต้นทุน และสุดท้ายอัลกอริทึม Gradient Descent

การถดถอยโลจิสติกคืออะไร?

Logistic Regression เป็นเพียงอัลกอริธึมการจัดหมวดหมู่ที่ใช้ในการทำนายหมวดหมู่ที่ไม่ต่อเนื่อง เช่น การคาดคะเนว่าเมลเป็น 'สแปม' หรือ 'ไม่ใช่สแปม'; ทำนายว่าตัวเลขที่ระบุเป็น '9' หรือ 'ไม่ใช่ 9' เป็นต้น เมื่อดูจากชื่อแล้ว คุณต้องคิดว่า ทำไมถึงตั้งชื่อว่า Regression?

เหตุผลก็คือ แนวคิดของการถดถอยโลจิสติกได้รับการพัฒนาโดยการปรับแต่งองค์ประกอบสองสามประการของอัลกอริธึมการถดถอยเชิงเส้นพื้นฐานที่ใช้ในปัญหาการถดถอย

การถดถอยโลจิสติกยังสามารถนำไปใช้กับปัญหาการจำแนกประเภทหลายคลาส (มากกว่าสองคลาส) แม้ว่าจะแนะนำให้ใช้อัลกอริธึมนี้สำหรับปัญหาการจำแนกไบนารีเท่านั้น

ฟังก์ชันซิกมอยด์

ปัญหาการจำแนกประเภทไม่ใช่ปัญหาของฟังก์ชันเชิงเส้น เอาต์พุตจำกัดเฉพาะค่าที่ไม่ต่อเนื่องบางค่า เช่น 0 และ 1 สำหรับปัญหาการจำแนกประเภทไบนารี มันไม่สมเหตุสมผลเลยที่ฟังก์ชันเชิงเส้นจะคาดการณ์ค่าเอาต์พุตของเราว่ามากกว่า 1 หรือน้อยกว่า 0 ดังนั้นเราจึงจำเป็นต้องมีฟังก์ชันที่เหมาะสมเพื่อแสดงค่าเอาต์พุตของเรา

Sigmoid Function ช่วยแก้ปัญหาของเราได้ หรือที่เรียกว่า Logistic Function เป็นฟังก์ชันรูปตัว S ที่จับคู่ตัวเลขค่าจริงใดๆ กับช่วง (0,1) ซึ่งทำให้มีประโยชน์มากในการแปลงฟังก์ชันสุ่มใดๆ ให้เป็นฟังก์ชันตามการจำแนกประเภท ฟังก์ชันซิกมอยด์มีลักษณะดังนี้:

ฟังก์ชันซิกมอยด์

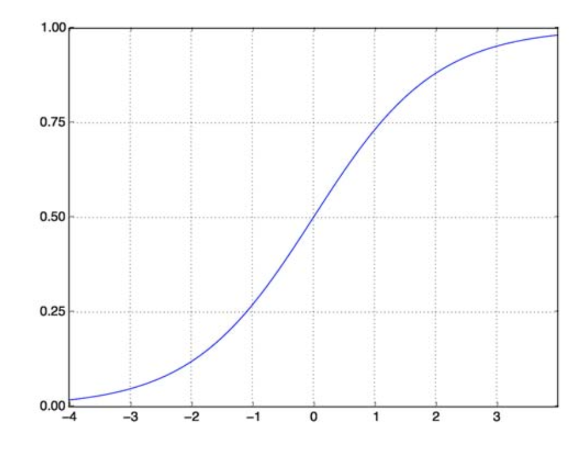
แหล่งที่มา

ตอนนี้รูปแบบทางคณิตศาสตร์ของฟังก์ชัน sigmoid สำหรับเวกเตอร์พารามิเตอร์และเวกเตอร์อินพุต X คือ:

(z) = 11+exp(-z) โดยที่ z = TX

(z) จะให้ความน่าจะเป็นที่ผลลัพธ์เป็น 1 อย่างที่เราทราบกันดีว่าค่าความน่าจะเป็นมีตั้งแต่ 0 ถึง 1 ทีนี้ นี่ไม่ใช่ผลลัพธ์ที่เราต้องการสำหรับปัญหาการจำแนกประเภทแบบแยกส่วน (0 และ 1 เท่านั้น) . ตอนนี้เราสามารถเปรียบเทียบความน่าจะเป็นที่คาดการณ์ไว้กับ 0.5 หากความน่าจะเป็น > 0.5 เรามี y=1 ในทำนองเดียวกัน หากความน่าจะเป็น < 0.5 เราก็ได้ y=0

ฟังก์ชันต้นทุน

ตอนนี้เรามีการคาดคะเนแบบแยกส่วนแล้ว ก็ถึงเวลาตรวจสอบว่าการคาดคะเนของเรานั้นถูกต้องหรือไม่ ในการทำเช่นนั้น เรามีฟังก์ชันต้นทุน ฟังก์ชันต้นทุนเป็นเพียงผลรวมของข้อผิดพลาดทั้งหมดที่เกิดขึ้นในการคาดคะเนทั่วทั้งชุดข้อมูล แน่นอน เราไม่สามารถใช้ฟังก์ชันต้นทุนที่ใช้ในการถดถอยเชิงเส้นได้ ดังนั้น ฟังก์ชันต้นทุนใหม่สำหรับการถดถอยโลจิสติกคือ:

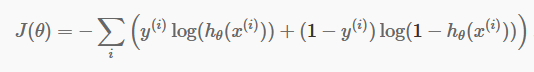แหล่งที่มา

อย่ากลัวสมการ มันง่ายมาก สำหรับการวนซ้ำแต่ละครั้ง i เป็นการคำนวณข้อผิดพลาดที่เราทำในการทำนายของเรา จากนั้นจึงรวมข้อผิดพลาดทั้งหมดเข้าด้วยกันเพื่อกำหนดฟังก์ชันต้นทุน J()

สองคำในวงเล็บนั้นจริงๆ แล้วสำหรับสองกรณี: y=0 และ y=1 เมื่อ y=0 เทอมแรกหายไป และเราเหลือเทอมที่สองเท่านั้น ในทำนองเดียวกัน เมื่อ y=1 เทอมที่สองหายไป และเราเหลือเพียงเทอมแรกเท่านั้น

อัลกอริทึมการไล่ระดับสี

เราคำนวณฟังก์ชันต้นทุนเรียบร้อยแล้ว แต่เราจำเป็นต้องลดการสูญเสียเพื่อสร้างอัลกอริธึมการทำนายที่ดี ในการทำเช่นนั้น เรามีอัลกอริธึม Gradient Descent

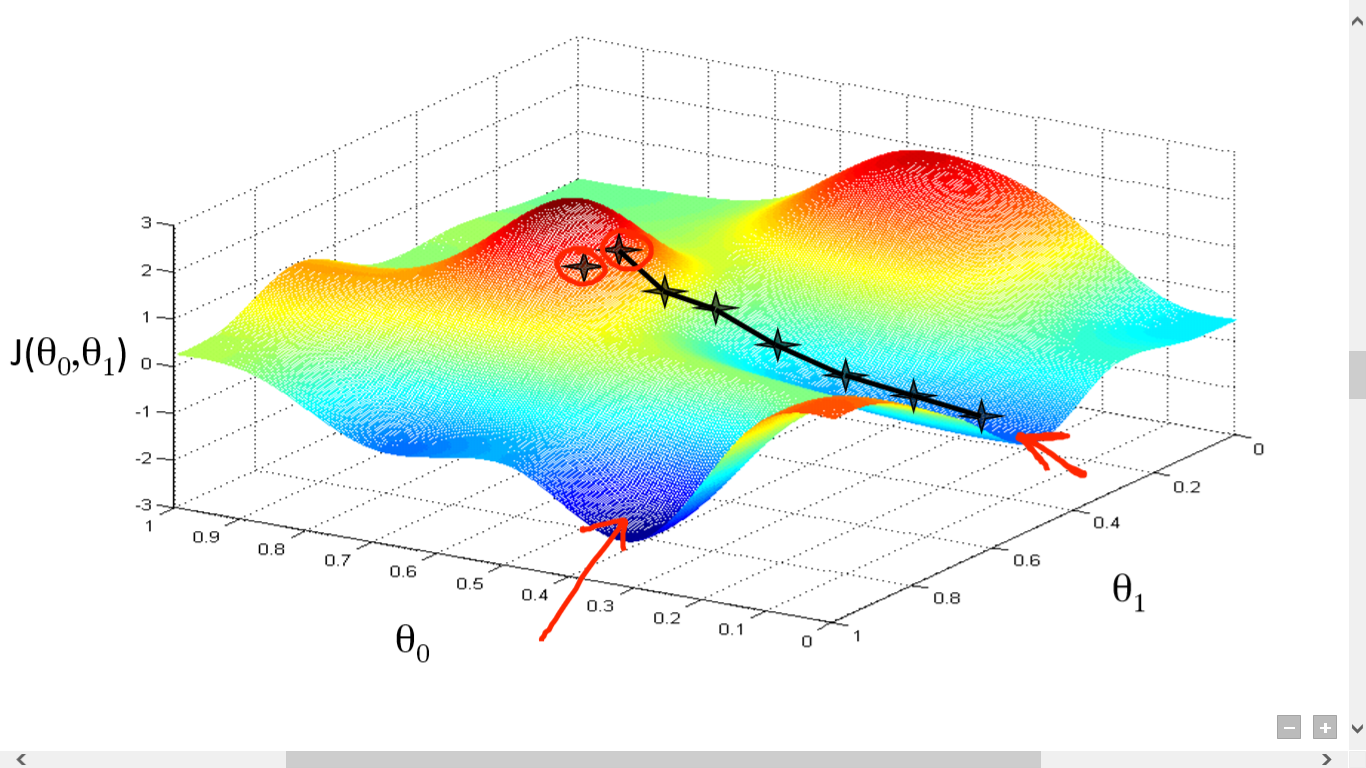แหล่งที่มา

ที่นี่เราได้พล็อตกราฟระหว่าง J()และ วัตถุประสงค์ของเราคือการหาจุดที่ลึกที่สุด (ต่ำสุดทั่วโลก) ของฟังก์ชันนี้ ตอนนี้จุดที่ลึกที่สุดคือจุดที่ J() เป็นค่าต่ำสุด

ต้องใช้สองสิ่งในการหาจุดที่ลึกที่สุด:

• Derivative – เพื่อค้นหาทิศทางของขั้นตอนต่อไป
• (อัตราการเรียนรู้) – ขนาดของขั้นตอนต่อไป

แนวคิดคือขั้นแรกให้คุณเลือกจุดสุ่มจากฟังก์ชัน จากนั้นคุณต้องคำนวณอนุพันธ์ของ J()wrt ซึ่งจะชี้ไปที่ทิศทางของท้องถิ่นขั้นต่ำ ตอนนี้คูณการไล่ระดับผลลัพธ์นั้นด้วยอัตราการเรียนรู้ อัตราการเรียนรู้ไม่มีค่าคงที่ และจะตัดสินจากปัญหา

ตอนนี้ คุณต้องลบผลลัพธ์เพื่อให้ได้ค่าใหม่

การอัปเดตนี้ควรทำพร้อมกันสำหรับทุกๆ (i )

ทำตามขั้นตอนเหล่านี้ซ้ำๆ จนกว่าจะถึงค่าขั้นต่ำระดับท้องถิ่นหรือระดับสากล เมื่อไปถึงระดับต่ำสุดทั่วโลก ถือว่าคุณขาดทุนน้อยที่สุดในการคาดการณ์ของคุณ

การหาอนุพันธ์เป็นเรื่องง่าย แค่แคลคูลัสพื้นฐานที่คุณต้องทำในโรงเรียนมัธยมปลายก็เพียงพอแล้ว ปัญหาหลักอยู่ที่อัตราการเรียนรู้ ( ) การเรียนให้ได้ดีเป็นสิ่งสำคัญและมักจะยาก

หากคุณใช้อัตราการเรียนรู้ที่น้อยมาก แต่ละขั้นตอนจะเล็กเกินไป และด้วยเหตุนี้ คุณจะใช้เวลานานมากในการเข้าถึงขั้นต่ำในท้องถิ่น

ตอนนี้ หากคุณมีแนวโน้มที่จะใช้ค่าอัตราการเรียนรู้จำนวนมาก คุณจะเกินค่าขั้นต่ำและจะไม่มาบรรจบกันอีกเลย ไม่มีกฎเกณฑ์เฉพาะสำหรับอัตราการเรียนรู้ที่สมบูรณ์แบบ

คุณต้องปรับแต่งเพื่อเตรียมโมเดลที่ดีที่สุด

สมการของ Gradient Descent คือ:

ทำซ้ำจนกระทั่งบรรจบกัน:

ดังนั้นเราสามารถสรุปอัลกอริธึม Gradient Descent ได้ดังนี้:

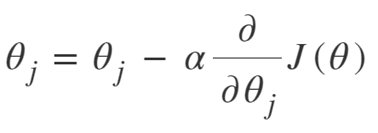
1. เริ่มด้วยการสุ่ม
2. วนซ้ำจนกว่าจะบรรจบกัน:
   1. การคำนวณไล่ระดับ
   2. อัปเดต
3. กลับ

อัลกอริทึมการไล่ระดับสีสุ่ม

ตอนนี้ Gradient Descent Algorithm เป็นอัลกอริธึมที่ดีในการย่อฟังก์ชันต้นทุนให้น้อยที่สุด โดยเฉพาะอย่างยิ่งสำหรับข้อมูลขนาดเล็กถึงขนาดกลาง แต่เมื่อเราต้องจัดการกับชุดข้อมูลที่ใหญ่ขึ้น อัลกอริธึม Gradient Descent จะคำนวณได้ช้า เหตุผลง่ายๆ คือ จำเป็นต้องคำนวณการไล่ระดับสี และอัปเดตค่าพร้อมกันสำหรับทุกพารามิเตอร์ และนั่นก็เช่นกันสำหรับตัวอย่างการฝึกทุกครั้ง

คิดเกี่ยวกับการคำนวณทั้งหมดเหล่านั้น! มันมีขนาดใหญ่มาก และด้วยเหตุนี้จึงมีความจำเป็นสำหรับอัลกอริธึม Gradient Descent ที่ได้รับการดัดแปลงเล็กน้อย กล่าวคือ – Stochastic Gradient Descent Algorithm (SGD)

ความแตกต่างเพียงอย่างเดียวที่ SGD มีกับ Normal Gradient Descent คือ ใน SGD เราไม่จัดการกับอินสแตนซ์การฝึกอบรมทั้งหมดในคราวเดียว ใน SGD เราคำนวณการไล่ระดับของฟังก์ชันต้นทุนสำหรับตัวอย่างสุ่มเพียงตัวอย่างเดียวในการวนซ้ำแต่ละครั้ง

การทำเช่นนี้จะลดเวลาที่ใช้ในการคำนวณลงอย่างมากโดยเฉพาะสำหรับชุดข้อมูลขนาดใหญ่ เส้นทางที่ SGD ดำเนินไปนั้นเป็นเส้นทางที่ไม่แน่นอนและมีเสียงดัง (แม้ว่าเส้นทางที่มีเสียงดังอาจทำให้เรามีโอกาสไปถึงจุดต่ำสุดของโลก)

แต่ไม่เป็นไรเพราะเราไม่ต้องกังวลกับเส้นทางที่เดิน

เราต้องสูญเสียน้อยที่สุดในเวลาที่เร็วขึ้นเท่านั้น

ดังนั้นเราสามารถสรุปอัลกอริธึม Gradient Descent ได้ดังนี้:

1. วนซ้ำจนกว่าจะบรรจบกัน:
   1. เลือกจุดข้อมูลเดียว ' i'
   2. คำนวณไล่ระดับบนจุดเดียวนั้น
   3. อัปเดต
2. กลับ

อัลกอริธึมการไล่ระดับการไล่สีแบบมินิแบทช์

Mini-Batch Gradient Descent เป็นการปรับเปลี่ยนเล็กน้อยของอัลกอริธึม Gradient Descent มันค่อนข้างอยู่ระหว่างการไล่ระดับสีปกติและการไล่ระดับสีสุ่ม

Mini-Batch Gradient Descent คือการนำชุดข้อมูลทั้งหมดที่มีขนาดเล็กลง แล้วลดการสูญเสียในชุดข้อมูลให้น้อยที่สุด

กระบวนการนี้มีประสิทธิภาพมากกว่าอัลกอริธึม Gradient Descent ทั้งสองด้านบน ตอนนี้ขนาดแบทช์สามารถเป็นอะไรก็ได้ที่คุณต้องการ

แต่นักวิจัยได้แสดงให้เห็นว่าจะดีกว่าถ้าคุณเก็บไว้ภายใน 1 ถึง 100 โดยที่ 32 เป็นขนาดแบทช์ที่ดีที่สุด

ดังนั้นขนาดชุดงาน = 32 จะถูกเก็บไว้เป็นค่าเริ่มต้นในกรอบงานส่วนใหญ่

1. วนซ้ำจนกว่าจะบรรจบกัน:
   1. เลือกชุดข้อมูล ' b ' จุดข้อมูล
   2. คำนวณการไล่ระดับสีในชุดนั้น
   3. อัปเดต
2. กลับ

บทสรุป

ตอนนี้คุณมีความเข้าใจเชิงทฤษฎีเกี่ยวกับการถดถอยโลจิสติกแล้ว คุณได้เรียนรู้วิธีแสดงฟังก์ชันลอจิสติกส์ทางคณิตศาสตร์แล้ว คุณทราบวิธีการวัดข้อผิดพลาดที่คาดการณ์ไว้โดยใช้ฟังก์ชันต้นทุน

คุณยังทราบวิธีลดการสูญเสียนี้โดยใช้อัลกอริธึม Gradient Descent

สุดท้าย คุณรู้ว่ารูปแบบใดของ Gradient Descent Algorithm ที่คุณควรเลือกสำหรับปัญหาของคุณ upGrad มอบ ประกาศนียบัตร PG ในการเรียนรู้ของเครื่องและ AI และ วิทยาศาสตรมหาบัณฑิตสาขาการเรียนรู้ด้วยเครื่องและ AI ที่อาจแนะนำคุณสู่การสร้างอาชีพ หลักสูตรเหล่านี้จะอธิบายความจำเป็นในการเรียนรู้ของเครื่องและขั้นตอนเพิ่มเติมในการรวบรวมความรู้ในโดเมนนี้ ซึ่งครอบคลุมแนวคิดที่หลากหลายตั้งแต่ อัลกอริทึมการไล่ระดับสีแบบไล่ระดับ ไปจนถึง Neural Networks