逻辑回归中的梯度下降[为初学者解释]

在本文中，我们将讨论逻辑回归中非常流行的梯度下降算法。 我们将研究什么是逻辑回归，然后逐步转向逻辑回归方程、成本函数，最后是梯度下降算法。

什么是逻辑回归？

逻辑回归只是一种用于预测离散类别的分类算法，例如预测邮件是“垃圾邮件”还是“非垃圾邮件”； 预测给定数字是“9”还是“非 9”等。现在，通过查看名称，您一定会想，为什么将其命名为 Regression？

原因是，逻辑回归的想法是通过调整回归问题中使用的基本线性回归算法的一些元素而发展起来的。

逻辑回归也可以应用于多类（多于两个类）分类问题。 虽然，建议仅将此算法用于二元分类问题。

Sigmoid 函数

分类问题不是线性函数问题。 输出仅限于某些离散值，例如二进制分类问题的 0 和 1。 线性函数预测我们的输出值大于 1 或小于 0 是没有意义的。所以我们需要一个合适的函数来表示我们的输出值。

Sigmoid 函数解决了我们的问题。 也称为 Logistic 函数，它是一个 S 形函数，将任何实数值数映射到 (0,1) 区间，因此在将任何随机函数转换为基于分类的函数时非常有用。 Sigmoid 函数如下所示：

Sigmoid 函数

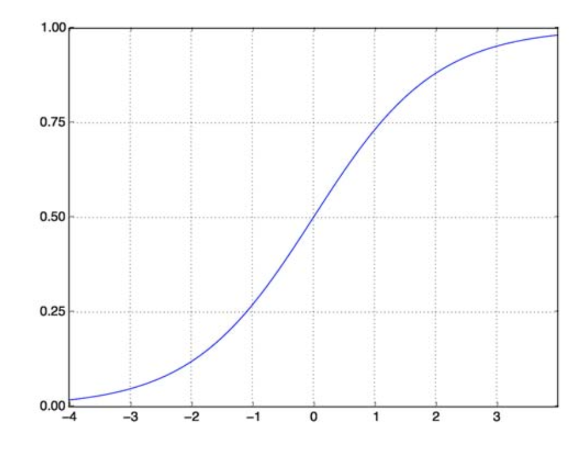
资源

现在参数化向量和输入向量 X 的 sigmoid 函数的数学形式是：

(z) = 11+exp(-z) 其中 z = TX

(z) 将给出输出为 1 的概率。众所周知，概率值的范围从 0 到 1。现在，对于基于离散（仅 0 和 1）的分类问题，这不是我们想要的输出. 所以现在我们可以将预测概率与 0.5 进行比较。 如果概率 > 0.5，我们有 y=1。 类似地，如果概率 < 0.5，我们有 y=0。

成本函数

现在我们有了离散预测，是时候检查我们的预测是否确实正确。 为此，我们有一个成本函数。 成本函数仅仅是整个数据集的预测中所有错误的总和。 当然，我们不能使用线性回归中使用的成本函数。 所以逻辑回归的新成本函数是：

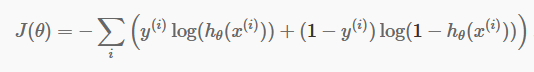资源

不要害怕等式。 这很简单。 对于每次迭代i ，它都会计算我们在预测中产生的误差，然后将所有误差相加来定义我们的成本函数 J()。

括号内的两项实际上是针对两种情况：y=0 和 y=1。 当 y=0 时，第一项消失，我们只剩下第二项。 同样，当 y=1 时，第二项消失，我们只剩下第一项。

梯度下降算法

我们已经成功计算了我们的成本函数。 但是我们需要最小化损失来做出一个好的预测算法。 为此，我们有梯度下降算法。

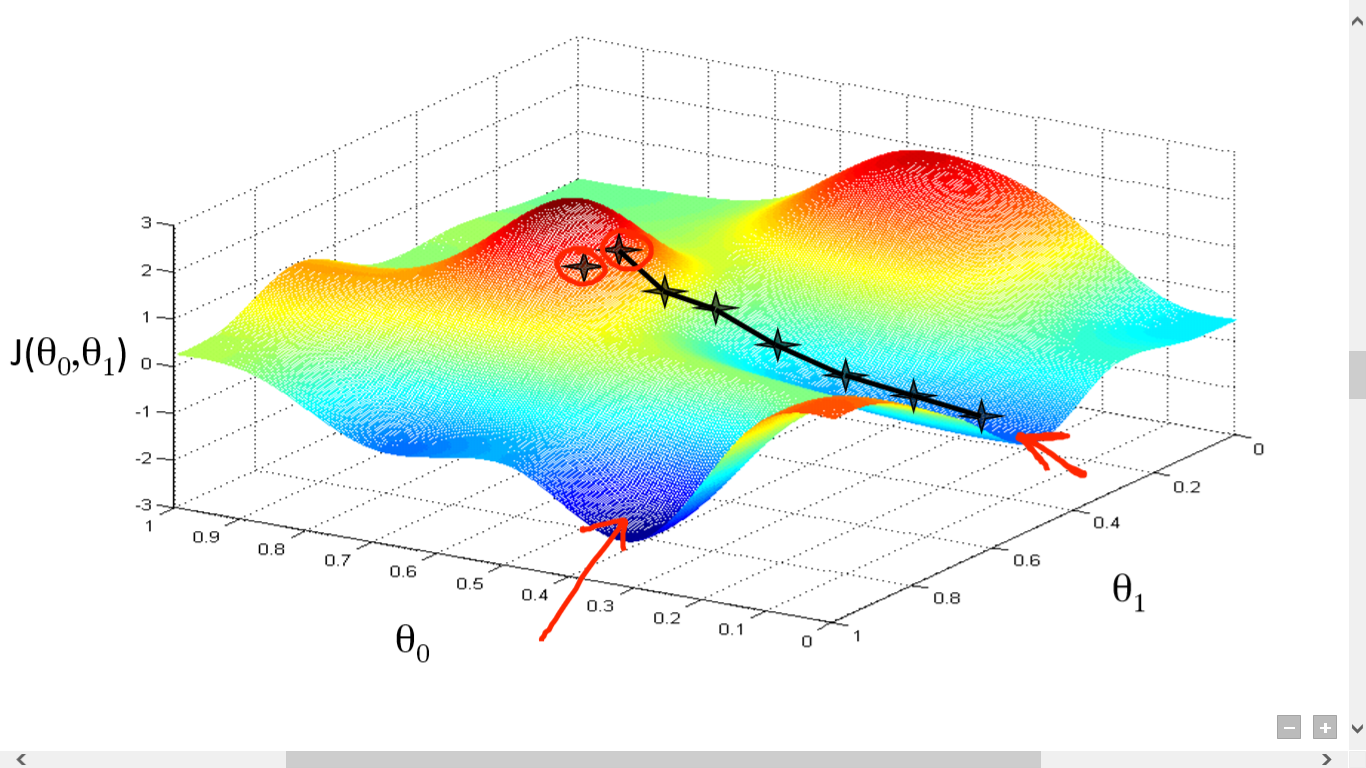资源

在这里，我们在 J() 和 之间绘制了一个图表。 我们的目标是找到这个函数的最深点（全局最小值）。 现在最深点是 J() 最小的地方。

找到最深点需要两件事：

• 导数——寻找下一步的方向。
• （学习率）——下一步的幅度

这个想法是你首先从函数中选择任何随机点。 然后你需要计算 J()wrt 的导数。 这将指向局部最小值的方向。 现在将结果梯度与学习率相乘。 学习率没有固定值，要根据问题来决定。

现在，您需要从中减去结果以获得新的 .

这个更新应该同时为每个 (i) 完成。

重复执行这些步骤，直到达到局部或全局最小值。 通过达到全局最小值，您在预测中实现了尽可能低的损失。

取衍生品很简单。 只要你在高中必须完成的基本微积分就足够了。 主要问题在于学习率（）。 采用良好的学习率很重要，而且通常很困难。

如果您采用非常小的学习率，每一步都会太小，因此您将花费大量时间来达到局部最小值。

现在，如果你倾向于采用一个巨大的学习率值，你将超过最小值并且永远不会再次收敛。 完美的学习率没有特定的规则。

您需要对其进行调整以准备最佳模型。

梯度下降的方程是：

重复直到收敛：

所以我们可以将梯度下降算法总结为：

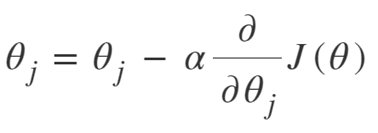
1. 从随机开始
2. 循环直到收敛：
   1. 计算梯度
   2. 更新
3. 返回

随机梯度下降算法

现在，梯度下降算法是最小化成本函数的一种很好的算法，特别是对于中小型数据。 但是当我们需要处理更大的数据集时，梯度下降算法的计算速度会很慢。 原因很简单：它需要计算梯度，并同时更新每个参数的值，每个训练样本也是如此。

所以想想所有这些计算！ 它很大，因此需要稍微修改一下梯度下降算法，即——随机梯度下降算法（SGD）。

SGD 与 Normal Gradient Descent 的唯一区别在于，在 SGD 中，我们不会一次处理整个训练实例。 在 SGD 中，我们在每次迭代中仅计算单个随机示例的成本函数的梯度。

现在，这样做可以大大减少计算所需的时间，尤其是对于大型数据集。 SGD 采用的路径非常随意且嘈杂（尽管嘈杂的路径可能使我们有机会达到全局最小值）。

但这没关系，因为我们不必担心所走的路。

我们只需要在更快的时间内达到最小的损失。

所以我们可以将梯度下降算法总结为：

1. 循环直到收敛：
   1. 选择单个数据点“ i”
   2. 在该单点上计算梯度
   3. 更新
2. 返回

小批量梯度下降算法

Mini-Batch Gradient Descent 是对 Gradient Descent 算法的另一个轻微修改。 它介于正常梯度下降和随机梯度下降之间。

Mini-Batch Gradient Descent 只是取整个数据集的一小部分，然后最小化它的损失。

这个过程比上述两种梯度下降算法都更有效。 现在批量大小当然可以是你想要的任何东西。

但研究人员表明，最好将其保持在 1 到 100 之间，其中 32 是最佳批量大小。

因此，在大多数框架中，batch size = 32 保持默认。

1. 循环直到收敛：
   1. 选择一批“ b ”个数据点
   2. 计算该批次的梯度
   3. 更新
2. 返回

结论

现在你对逻辑回归有了理论上的理解。 您已经学习了如何以数学方式表示逻辑函数。 您知道如何使用成本函数来衡量预测误差。

您还知道如何使用梯度下降算法将这种损失降至最低。

最后，您知道应该为您的问题选择哪种梯度下降算法变体。 upGrad 提供机器学习和人工智能的PG 文凭和机器学习和人工智能的理学硕士，可以指导您建立职业生涯。 这些课程将解释机器学习的必要性以及收集该领域知识的进一步步骤，涵盖从梯度下降算法到神经网络的各种概念。