هبوط الانحدار في الانحدار اللوجستي [شرح للمبتدئين]

في هذه المقالة ، سنناقش خوارزمية نزول التدرج المشهورة جدًا في الانحدار اللوجستي. سننظر في ماهية الانحدار اللوجستي ، ثم ننتقل تدريجياً إلى معادلة الانحدار اللوجستي ، ووظيفة التكلفة ، وأخيراً خوارزمية الانحدار التدريجي.

ما هو الانحدار اللوجستي؟

الانحدار اللوجستي هو ببساطة خوارزمية تصنيف تُستخدم للتنبؤ بالفئات المنفصلة ، مثل التنبؤ بما إذا كان البريد "بريدًا عشوائيًا" أم "ليس بريدًا عشوائيًا" ؛ توقع ما إذا كان رقم معين هو "9" أم "ليس 9" وما إلى ذلك. الآن ، من خلال النظر إلى الاسم ، يجب أن تفكر ، لماذا يسمى الانحدار؟

والسبب هو أن فكرة الانحدار اللوجستي تم تطويرها من خلال تعديل بعض عناصر خوارزمية الانحدار الخطي الأساسية المستخدمة في مشاكل الانحدار.

يمكن أيضًا تطبيق الانحدار اللوجستي على مشاكل التصنيف متعدد الفئات (أكثر من فئتين). على الرغم من أنه يوصى باستخدام هذه الخوارزمية لمشاكل التصنيف الثنائي فقط.

وظيفة السيني

مشاكل التصنيف ليست مشاكل دالة خطية. الإخراج يقتصر على قيم منفصلة معينة ، على سبيل المثال ، 0 و 1 لمشكلة تصنيف ثنائي. ليس من المنطقي أن تتنبأ دالة خطية بقيم مخرجاتنا على أنها أكبر من 1 ، أو أقل من 0. لذلك نحن بحاجة إلى دالة مناسبة لتمثيل قيم المخرجات.

وظيفة السيني تحل مشكلتنا. تُعرف أيضًا باسم الوظيفة اللوجيستية ، وهي دالة على شكل حرف S ترسم أي رقم قيمة حقيقية إلى فاصل زمني (0،1) ، مما يجعلها مفيدة جدًا في تحويل أي وظيفة عشوائية إلى وظيفة قائمة على التصنيف. تبدو الوظيفة السينية كما يلي:

وظيفة السيني

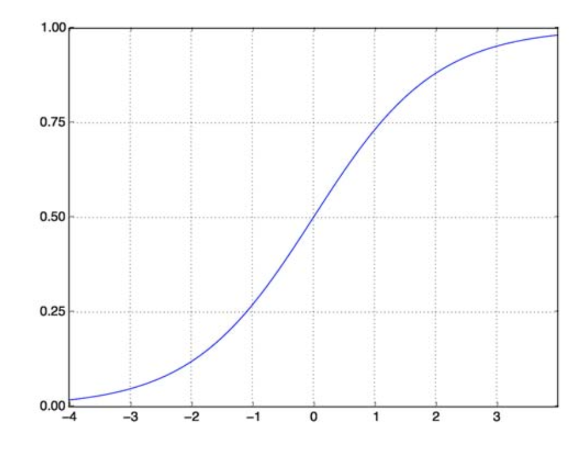
مصدر

الآن الشكل الرياضي للدالة السينية للمتجه المحدد ومتجه الإدخال X هو:

(ض) = 11 + exp (-z) حيث z = TX

(ض) ستعطينا احتمال أن يكون الناتج 1. كما نعلم جميعًا ، تتراوح قيمة الاحتمال من 0 إلى 1. الآن ، هذا ليس الناتج الذي نريده لمشكلة التصنيف المنفصلة (0 و 1 فقط) . يمكننا الآن مقارنة الاحتمال المتوقع بـ 0.5. إذا كان الاحتمال> 0.5 ، لدينا y = 1. وبالمثل ، إذا كان الاحتمال <0.5 ، لدينا y = 0.

دالة التكلفه

الآن وقد أصبح لدينا تنبؤاتنا المنفصلة ، فقد حان الوقت للتحقق مما إذا كانت تنبؤاتنا صحيحة أم لا. للقيام بذلك ، لدينا وظيفة التكلفة. دالة التكلفة هي مجرد تجميع لجميع الأخطاء التي حدثت في التنبؤات عبر مجموعة البيانات بأكملها. بالطبع ، لا يمكننا استخدام دالة التكلفة المستخدمة في الانحدار الخطي. لذا فإن دالة التكلفة الجديدة للانحدار اللوجستي هي:

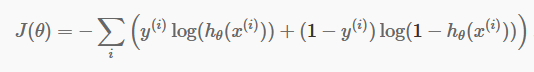مصدر

لا تخافوا من المعادلة. أنها بسيطة جدا. لكل تكرار i ، يتم حساب الخطأ الذي ارتكبناه في تنبؤنا ، ثم نجمع جميع الأخطاء لتحديد دالة التكلفة J ().

المصطلحان الموجودان داخل القوس هما في الواقع للحالتين: y = 0 و y = 1. عندما y = 0 ، يختفي الحد الأول ويتبقى لنا الحد الثاني فقط. وبالمثل ، عندما y = 1 ، يختفي الحد الثاني ، ويتبقى لنا الحد الأول فقط.

خوارزمية نزول التدرج

لقد نجحنا في حساب دالة التكلفة الخاصة بنا. لكننا بحاجة لتقليل الخسارة لعمل خوارزمية تنبؤ جيدة. للقيام بذلك ، لدينا خوارزمية النسب المتدرج.

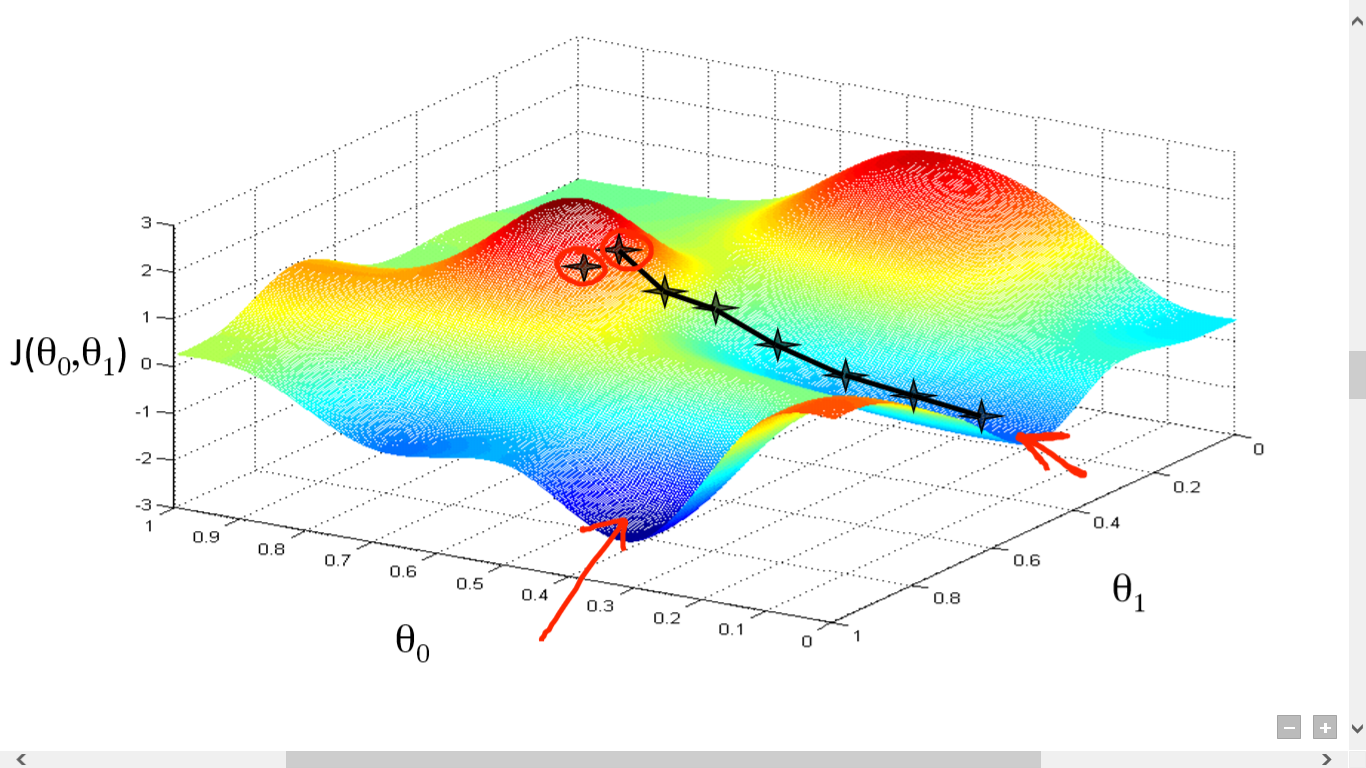مصدر

هنا قمنا برسم رسم بياني بين J () و. هدفنا هو إيجاد أعمق نقطة (الحد الأدنى العالمي) لهذه الوظيفة. الآن أعمق نقطة هي حيث J () هي الحد الأدنى.

مطلوب شيئين للعثور على أعمق نقطة:

• مشتق - لإيجاد اتجاه الخطوة التالية.
• (معدل التعلم) - حجم الخطوة التالية

الفكرة هي أولاً تحديد أي نقطة عشوائية من الوظيفة. ثم تحتاج إلى حساب مشتق J () wrt. سيشير هذا إلى اتجاه الحد الأدنى المحلي. الآن اضرب هذا التدرج الناتج في معدل التعلم. معدل التعلم ليس له قيمة ثابتة ، ويتم تحديده بناءً على المشكلات.

الآن ، تحتاج إلى طرح النتيجة من للحصول على الجديد.

يجب إجراء هذا التحديث في نفس الوقت لكل (i) .

كرر هذه الخطوات بشكل متكرر حتى تصل إلى الحد الأدنى المحلي أو العالمي. من خلال الوصول إلى الحد الأدنى العالمي ، تكون قد حققت أقل خسارة ممكنة في توقعك.

أخذ المشتقات بسيط. يكفي فقط حساب التفاضل والتكامل الأساسي الذي يجب أن تكون قد قمت به في مدرستك الثانوية. القضية الرئيسية هي مع معدل التعلم (). يعتبر الحصول على معدل تعليمي جيد أمرًا مهمًا وصعبًا في كثير من الأحيان.

إذا كنت تأخذ معدل تعلم صغيرًا جدًا ، فستكون كل خطوة صغيرة جدًا ، وبالتالي ستستغرق الكثير من الوقت للوصول إلى الحد الأدنى المحلي.

الآن ، إذا كنت تميل إلى الحصول على قيمة كبيرة لمعدل التعلم ، فسوف تتجاوز الحد الأدنى ولن تتقارب مرة أخرى أبدًا. لا توجد قاعدة محددة لمعدل التعلم المثالي.

تحتاج إلى تعديله لإعداد أفضل نموذج.

معادلة الانحدار هي:

كرر حتى التقارب:

لذلك يمكننا تلخيص خوارزمية النسب المتدرج على النحو التالي:

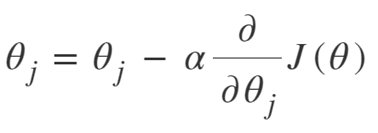
1. ابدأ بعشوائية
2. التكرار حتى التقارب:
   1. حساب التدرج
   2. تحديث
3. إرجاع

خوارزمية نزول التدرج العشوائي

الآن ، تعد خوارزمية Gradient Descent خوارزمية دقيقة لتقليل دالة التكلفة ، خاصة للبيانات الصغيرة إلى المتوسطة. ولكن عندما نحتاج إلى التعامل مع مجموعات بيانات أكبر ، يتبين أن خوارزمية هبوط التدرج تكون بطيئة في الحساب. السبب بسيط: يحتاج إلى حساب التدرج ، وتحديث القيم في وقت واحد لكل معلمة ، وهذا أيضًا لكل مثال تدريب.

لذا فكر في كل تلك الحسابات! إنه ضخم ، وبالتالي كانت هناك حاجة إلى خوارزمية نزول متدرج معدلة قليلاً ، وهي - خوارزمية نزول التدرج العشوائي (SGD).

الفارق الوحيد بين SGD و Normal Gradient Descent هو أننا في SGD لا نتعامل مع مثيل التدريب بأكمله في وقت واحد. في SGD ، نحسب تدرج دالة التكلفة لمثال عشوائي واحد فقط في كل تكرار.

الآن ، يؤدي القيام بذلك إلى تقليل الوقت الذي تستغرقه العمليات الحسابية بهامش ضخم خاصة لمجموعات البيانات الكبيرة. المسار الذي سلكته SGD عشوائي للغاية وصاخب (على الرغم من أن المسار الصاخب قد يمنحنا فرصة للوصول إلى الحد الأدنى العالمي).

لكن هذا جيد ، حيث لا داعي للقلق بشأن المسار الذي نسلكه.

نحن بحاجة فقط للوصول إلى الحد الأدنى من الخسائر في وقت أسرع.

لذلك يمكننا تلخيص خوارزمية النسب المتدرج على النحو التالي:

1. التكرار حتى التقارب:
   1. اختر نقطة بيانات واحدة " i"
   2. حساب التدرج فوق تلك النقطة المفردة
   3. تحديث
2. إرجاع

خوارزمية نزول الدفعة الصغيرة

نزول الدفعة الصغيرة هو تعديل طفيف آخر لخوارزمية نزول التدرج. يقع إلى حد ما بين نزول متدرج عادي ونسب متدرج عشوائي.

يأخذ Mini-Batch Gradient Descent فقط مجموعة أصغر من مجموعة البيانات بأكملها ، ثم يقلل الخسارة عليها.

هذه العملية أكثر كفاءة من خوارزميات النسب المتدرج المذكورتين أعلاه. الآن يمكن أن يكون حجم الدفعة بالطبع أي شيء تريده.

لكن الباحثين أظهروا أنه من الأفضل أن تحتفظ بها في حدود 1 إلى 100 ، مع كون 32 هو أفضل حجم للدفعة.

ومن ثم يتم الاحتفاظ بحجم الدُفعة = 32 افتراضيًا في معظم الأطر.

1. التكرار حتى التقارب:
   1. اختر مجموعة من نقاط البيانات " ب "
   2. حساب التدرج على تلك الدفعة
   3. تحديث
2. إرجاع

خاتمة

الآن لديك الفهم النظري للانحدار اللوجستي. لقد تعلمت كيفية تمثيل الوظيفة اللوجستية رياضيًا. أنت تعرف كيفية قياس الخطأ المتوقع باستخدام دالة التكلفة.

أنت تعرف أيضًا كيف يمكنك تقليل هذه الخسارة باستخدام خوارزمية Gradient Descent.

أخيرًا ، تعرف أي شكل من أشكال خوارزمية نزول التدرج يجب أن تختاره لمشكلتك. تقدم upGrad دبلوم PG في التعلم الآلي والذكاء الاصطناعي وماجستير العلوم في التعلم الآلي والذكاء الاصطناعي الذي قد يوجهك نحو بناء مستقبل مهني. ستشرح هذه الدورات الحاجة إلى التعلم الآلي والخطوات الإضافية لجمع المعرفة في هذا المجال التي تغطي مفاهيم متنوعة تتراوح من خوارزميات النسب المتدرج إلى الشبكات العصبية.