Descente de gradient dans la régression logistique [expliquée pour les débutants]

Dans cet article, nous discuterons du très populaire algorithme de descente de gradient dans la régression logistique. Nous examinerons ce qu'est la régression logistique, puis passerons progressivement à l'équation de la régression logistique, à sa fonction de coût et enfin à l'algorithme de descente de gradient.

Qu'est-ce que la régression logistique ?

La régression logistique est simplement un algorithme de classification utilisé pour prédire des catégories discrètes, comme prédire si un e-mail est un "spam" ou "pas un spam" ; prédire si un chiffre donné est un '9' ou 'pas 9' etc. Maintenant, en regardant le nom, vous devez vous demander pourquoi est-il nommé Régression ?

La raison en est que l'idée de la régression logistique a été développée en modifiant quelques éléments de l'algorithme de régression linéaire de base utilisé dans les problèmes de régression.

La régression logistique peut également être appliquée aux problèmes de classification multi-classes (plus de deux classes). Cependant, il est recommandé d'utiliser cet algorithme uniquement pour les problèmes de classification binaire.

Fonction sigmoïde

Les problèmes de classification ne sont pas des problèmes de fonction linéaire. La sortie est limitée à certaines valeurs discrètes, par exemple 0 et 1 pour un problème de classification binaire. Cela n'a pas de sens pour une fonction linéaire de prédire nos valeurs de sortie comme étant supérieures à 1 ou inférieures à 0. Nous avons donc besoin d'une fonction appropriée pour représenter nos valeurs de sortie.

La fonction sigmoïde résout notre problème. Également connue sous le nom de fonction logistique, il s'agit d'une fonction en forme de S mappant n'importe quel nombre de valeurs réelles sur un intervalle (0,1), ce qui la rend très utile pour transformer n'importe quelle fonction aléatoire en une fonction basée sur la classification. Une fonction sigmoïde ressemble à ceci :

Fonction sigmoïde

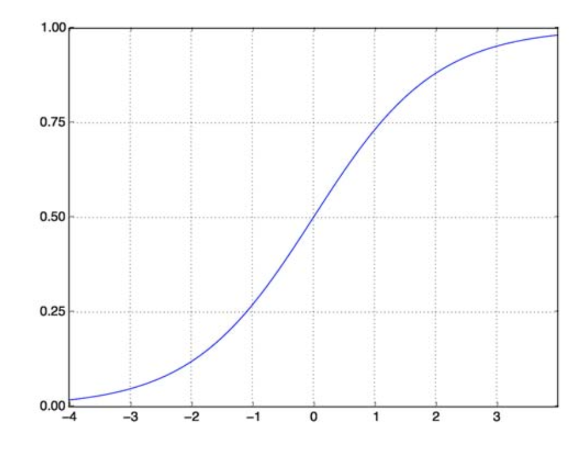
la source

Maintenant, la forme mathématique de la fonction sigmoïde pour le vecteur paramétré et le vecteur d'entrée X est :

(z) = 11+exp(-z) où z = TX

(z) nous donnera la probabilité que la sortie soit 1. Comme nous le savons tous, la valeur de probabilité varie de 0 à 1. Maintenant, ce n'est pas la sortie que nous voulons pour notre problème de classification discret (0 et 1 uniquement) . Nous pouvons donc maintenant comparer la probabilité prédite avec 0,5. Si probabilité > 0,5, on a y=1. De même, si la probabilité est < 0,5, nous avons y=0.

Fonction de coût

Maintenant que nous avons nos prédictions discrètes, il est temps de vérifier si nos prédictions sont effectivement correctes ou non. Pour ce faire, nous avons une fonction de coût. La fonction de coût est simplement la somme de toutes les erreurs commises dans les prédictions sur l'ensemble de l'ensemble de données. Bien sûr, nous ne pouvons pas utiliser la fonction de coût utilisée dans la régression linéaire. Ainsi, la nouvelle fonction de coût pour la régression logistique est :

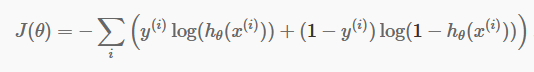la source

N'ayez pas peur de l'équation. C'est très simple. Pour chaque itération i , il calcule l'erreur que nous avons commise dans notre prédiction, puis additionne toutes les erreurs pour définir notre fonction de coût J().

Les deux termes à l'intérieur de la parenthèse sont en fait pour les deux cas : y=0 et y=1. Lorsque y=0, le premier terme s'annule et il ne nous reste plus que le second terme. De même, lorsque y = 1, le second terme s'annule et il ne nous reste plus que le premier terme.

Algorithme de descente de gradient

Nous avons calculé avec succès notre fonction de coût. Mais nous devons minimiser la perte pour faire un bon algorithme de prédiction. Pour ce faire, nous avons l'algorithme de descente de gradient.

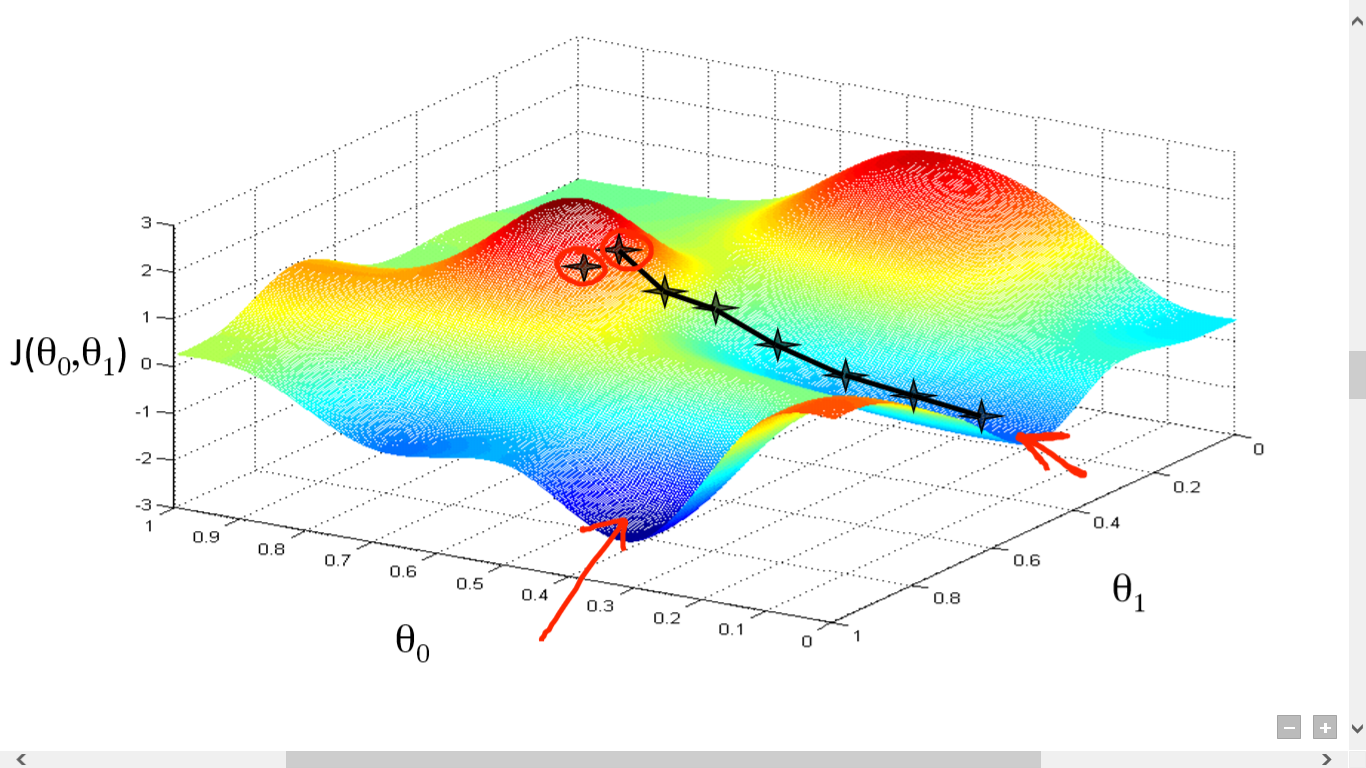la source

Ici, nous avons tracé un graphique entre J() et . Notre objectif est de trouver le point le plus profond (minimum global) de cette fonction. Maintenant, le point le plus profond est celui où le J() est minimum.

Deux choses sont nécessaires pour trouver le point le plus profond :

• Dérivée - pour trouver la direction de l'étape suivante.
• (Taux d'apprentissage) - ampleur de la prochaine étape

L'idée est que vous sélectionnez d'abord n'importe quel point aléatoire de la fonction. Ensuite, vous devez calculer la dérivée de J()wrt . Cela indiquera la direction du minimum local. Multipliez maintenant ce gradient résultant avec le taux d'apprentissage. Le taux d'apprentissage n'a pas de valeur fixe et doit être décidé en fonction des problèmes.

Maintenant, vous devez soustraire le résultat de pour obtenir le nouveau .

Cette mise à jour de doit être effectuée simultanément pour chaque (i) .

Effectuez ces étapes à plusieurs reprises jusqu'à ce que vous atteigniez le minimum local ou global. En atteignant le minimum global, vous avez atteint la perte la plus faible possible dans votre prédiction.

Prendre des dérivées est simple. Juste le calcul de base que vous devez avoir fait dans votre lycée est suffisant. Le problème majeur concerne le taux d'apprentissage ( ). Prendre un bon rythme d'apprentissage est important et souvent difficile.

Si vous prenez un très petit taux d'apprentissage, chaque étape sera trop petite, et donc vous prendrez beaucoup de temps pour atteindre le minimum local.

Maintenant, si vous avez tendance à prendre une valeur de taux d'apprentissage énorme, vous dépasserez le minimum et ne convergerez plus jamais. Il n'y a pas de règle spécifique pour le taux d'apprentissage parfait.

Vous devez le peaufiner pour préparer le meilleur modèle.

L'équation de Gradient Descent est :

Répéter jusqu'à convergence :

Nous pouvons donc résumer l'algorithme de descente de gradient comme suit :

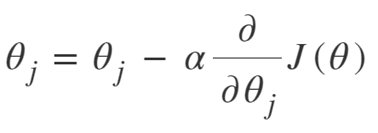
1. Commencez au hasard
2. Boucle jusqu'à convergence :
   1. Calculer le gradient
   2. Mettre à jour
3. Retourner

Algorithme de descente de gradient stochastique

Maintenant, Gradient Descent Algorithm est un algorithme fin pour minimiser la fonction de coût, en particulier pour les données petites à moyennes. Mais lorsque nous devons traiter des ensembles de données plus volumineux, l'algorithme de descente de gradient s'avère lent en termes de calcul. La raison est simple : il doit calculer le gradient et mettre à jour les valeurs simultanément pour chaque paramètre, et cela aussi pour chaque exemple de formation.

Pensez donc à tous ces calculs ! C'est énorme, et donc il y avait un besoin d'un algorithme de descente de gradient légèrement modifié, à savoir - Stochastic Gradient Descent Algorithm (SGD).

La seule différence entre SGD et Normal Gradient Descent est que, dans SGD, nous ne traitons pas l'intégralité de l'instance d'entraînement en une seule fois. Dans SGD, nous calculons le gradient de la fonction de coût pour un seul exemple aléatoire à chaque itération.

Désormais, cela réduit considérablement le temps de calcul, en particulier pour les grands ensembles de données. Le chemin emprunté par SGD est très aléatoire et bruyant (bien qu'un chemin bruyant puisse nous donner une chance d'atteindre les minima globaux).

Mais ce n'est pas grave, puisque nous n'avons pas à nous soucier du chemin parcouru.

Nous avons seulement besoin d'atteindre une perte minimale à un moment plus rapide.

Nous pouvons donc résumer l'algorithme de descente de gradient comme suit :

1. Boucle jusqu'à convergence :
   1. Choisissez un seul point de données ' i'
   2. Calculer le gradient sur ce point unique
   3. Mettre à jour
2. Retourner

Algorithme de descente de gradient en mini-lot

La descente de gradient en mini-lot est une autre légère modification de l'algorithme de descente de gradient. Il se situe quelque peu entre la descente de gradient normale et la descente de gradient stochastique.

Mini-Batch Gradient Descent prend simplement un plus petit lot de l'ensemble de données, puis minimise la perte sur celui-ci.

Ce processus est plus efficace que les deux algorithmes de descente de gradient ci-dessus. Maintenant, la taille du lot peut être bien sûr tout ce que vous voulez.

Mais les chercheurs ont montré qu'il est préférable de le maintenir entre 1 et 100, 32 étant la meilleure taille de lot.

Par conséquent, la taille du lot = 32 est conservée par défaut dans la plupart des frameworks.

1. Boucle jusqu'à convergence :
   1. Choisissez un lot de points de données « b »
   2. Calculer le gradient sur ce lot
   3. Mettre à jour
2. Retourner

Conclusion

Vous avez maintenant la compréhension théorique de la régression logistique. Vous avez appris à représenter mathématiquement la fonction logistique. Vous savez comment mesurer l'erreur prévue à l'aide de la fonction de coût.

Vous savez également comment vous pouvez minimiser cette perte en utilisant l'algorithme de descente de gradient.

Enfin, vous savez quelle variante de l'algorithme de descente de gradient vous devez choisir pour votre problème. upGrad fournit un diplôme PG en apprentissage automatique et IA et une maîtrise ès sciences en apprentissage automatique et IA qui peuvent vous guider vers la construction d'une carrière. Ces cours expliqueront la nécessité de l'apprentissage automatique et d'autres étapes pour rassembler des connaissances dans ce domaine couvrant des concepts variés allant des algorithmes de descente de gradient aux réseaux de neurones.