人工智能中的最小最大算法：組件、屬性、優勢和限制

AI 中的min max 算法，俗稱 minimax，是一種用於決策制定、博弈論和人工智能 (AI) 的回溯算法。 它用於為玩家找到最佳移動，假設對手也在最佳發揮。 國際象棋、井字遊戲、跳棋、圍棋等流行的兩人計算機或在線遊戲都使用此算法。

回溯算法用於找到計算問題的解決方案，使得候選者逐步朝著解決方案構建，一次一步。 未能完成解決方案的候選人將立即被放棄。

它是如何工作的？

在AI 中的 min max 算法中，有兩個玩家，Maximiser 和 Minimiser。 這兩個玩家在玩遊戲時都試圖獲得盡可能高的分數或最大的利益，而對手試圖獲得最低的分數或最小的利益。

每個遊戲板都有一個分配給它的評估分數，因此 Maximiser 將選擇最大值，而 Minimiser 將通過反動作選擇最小值。 如果 Maximiser 佔上風，則棋盤得分為正值，如果 Minimiser 佔上風，則棋盤得分為負值。

這是基於零和遊戲的概念，其中總效用得分在兩個玩家之間分配。 因此，一個玩家得分的增加會導致對手玩家得分的減少，從而使總得分始終為零。 因此，要讓一名球員獲勝，另一名球員必須輸球。

加入來自世界頂級大學的在線機器學習認證和 AI 課程。 獲得 Masters、Executive PGP 或 ACP 以加快您的職業生涯。

分解 AI 中的 min max 算法

在 AI 的 min max 算法中使用深度優先搜索算法探索完整的博弈樹。 它完全下到樹的終端節點，然後回溯到樹。

目標是為玩家找到可能的最佳移動。 這可以通過選擇具有最佳評估分數的節點來完成。 在評估對手的所有潛在動作後，將做出最佳選擇。 該算法會提前查看所有可能的值，直到最後並為玩家做出決定。

資源

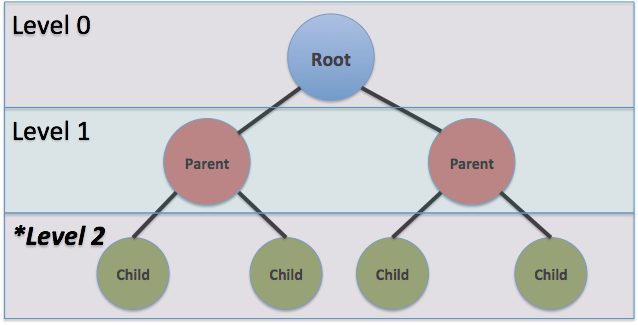
上面的博弈樹是一個嵌套數據結構，用於評估移動。 這裡的根節點是 0 級，它分支到 1 級或父節點，進一步分支到 2 級或子節點。 分支可以持續到多個層次，具有無限層次的潛力。 級別 0 就像棋盤的當前狀態，而級別 1 是棋盤的所有可能狀態，具體取決於下一步。

因此，如果玩家 2 已經移動，我們可以假設根節點是棋盤的當前狀態，等待玩家 1 的移動。 級別 1 節點包含玩家 1 的所有可能移動，級別 2 節點包含基於玩家 1 的每個可能移動的玩家 2 的所有可能移動。

考慮一個示例，其中有四個最終狀態，到達這些狀態的路徑是從樹的根到四個葉子。 四個葉子的值分別是左邊的3、6和右邊的4、7。 輪到 Maximiser/Player 1 採取行動了。 為了運行算法，必須對每一步做出假設。

如果玩家 1 選擇向左走，那麼 Minimiser/玩家 2 必須在 3 和 6 之間選擇最小的，所以他們會選擇 3。而如果玩家 1 選擇向右，玩家 2 將選擇 4，這是最小的4 和 7 這兩個值中的一個。因此，級別 1 現在具有值 3 和 4。

由於輪到玩家 1/Maximiser，他們必須選擇 1 級節點的最大值。 因此，他們會選擇 3。那麼最優選擇是向左走。

AI中的min max算法的步驟可以表述如下：

1. 創建整個遊戲樹。
2. 根據評估函數評估葉節點的分數。
3. 從葉子節點回溯到根節點：

對於 Maximizer，選擇得分最高的節點。

對於 Minimizer，選擇得分最低的節點。

4. 在根節點，選擇具有最大值的節點並選擇相應的移動。

另請閱讀：機器學習項目理念

AI 中 min max 算法的屬性

• 該算法是完整的，意味著在有限的搜索樹中，一定會找到解決方案。
• 如果兩個玩家都在最佳狀態下玩，那是最佳的。
• 由於博弈樹的深度優先搜索 (DFS)，算法的時間複雜度為 O(b m )，其中 b 是分支因子，m 是樹的最大深度。
• 與 DFS 一樣，該算法的空間複雜度為 O(bm)。

優點

• 對搜索空間進行全面評估。
• 人工智能中的決策很容易實現。
• 使用這種算法開發了新的智能機器。

限制

• 由於分支因子巨大，達到目標的過程較慢。
• 評估和搜索所有可能的節點和分支會降低引擎的性能和效率。
• 兩名球員都有太多的選擇需要決定。
• 如果有時間和空間的限制，是不可能探索整棵樹的。

但是使用 Alpha-Beta Pruning，可以改進算法。

結論

本文解釋了AI 中 min-max 算法的所有方面。 首先，介紹了該理論，並提供了使用位置的示例，然後描述了該算法在遊戲中的工作原理。

該算法被分解以解釋如何根據玩家的移動和反移動來做出做出最佳移動的決定。 然後列出算法的屬性。 最後，給出了該算法的優缺點。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和 AI 執行 PG 計劃，該計劃專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT -B 校友身份，5 個以上實用的實踐頂點項目和頂級公司的工作協助。