Алгоритм «минимум-максимум» в ИИ: компоненты, свойства, преимущества и ограничения

Алгоритм минимум-максимум в ИИ, широко известный как минимакс, представляет собой алгоритм обратного отслеживания, используемый в принятии решений, теории игр и искусственном интеллекте (ИИ). Он используется, чтобы найти оптимальный ход для игрока, предполагая, что противник также играет оптимально. Популярные компьютерные или онлайн-игры для двух игроков, такие как шахматы, крестики-нолики, шашки, го и т. д., используют этот алгоритм.

Алгоритм поиска с возвратом используется для поиска решения вычислительных задач таким образом, что кандидат постепенно приближается к решению, шаг за шагом. И кандидат, который не может завершить решение, немедленно отбрасывается.

Как это работает?

В алгоритме «минимум-максимум» в ИИ есть два игрока: «Максимайзер» и «Минимайзер». Оба этих игрока играют в игру, когда один пытается получить максимально возможное количество очков или максимальную выгоду, в то время как противник пытается получить наименьшее количество очков или минимальную выгоду.

Каждое игровое поле имеет присвоенный ему оценочный балл, поэтому максимайзер выберет максимальное значение, а минимайзер выберет минимизированное значение с помощью встречных ходов. Если Максимайзер имеет преимущество, то счет доски будет положительным, а если Минимайзер имеет преимущество, то счет доски будет отрицательным.

Это основано на концепции игры с нулевой суммой, в которой общая оценка полезности делится между двумя игроками. Таким образом, увеличение счета одного игрока приводит к уменьшению счета игрока-противника, в результате чего общий счет всегда равен нулю. Таким образом, чтобы один игрок выиграл, другой должен проиграть.

Присоединяйтесь к онлайн-курсам по сертификации машинного обучения и искусственному интеллекту от лучших университетов мира. Заработайте Masters, Executive PGP или ACP, чтобы ускорить свою карьеру.

Разбираем алгоритм минимум-максимум в ИИ

Полное игровое дерево исследуется с помощью алгоритма поиска в глубину в алгоритме минимум-максимум в ИИ. Он полностью спускается к конечному узлу дерева, а затем возвращается обратно по дереву.

Цель состоит в том, чтобы найти лучший возможный ход для игрока. Это можно сделать, выбрав узел с наилучшей оценочной оценкой. Лучший выбор будет сделан после оценки всех возможных ходов соперника. Алгоритм просматривает все возможные значения до конца и принимает решение за игрока.

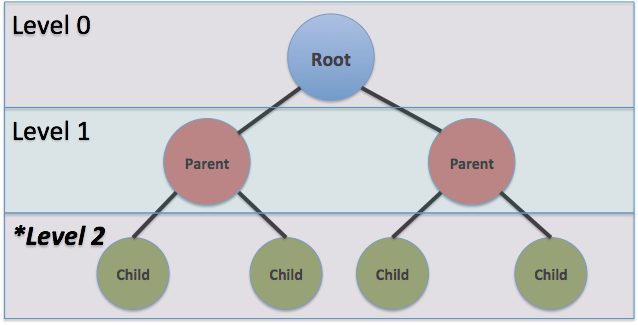
Источник

Приведенное выше дерево игры представляет собой вложенную структуру данных, которая используется для оценки ходов. Здесь корневым узлом является уровень 0, который разветвляется на уровень 1 или родительские узлы, которые далее разветвляются на уровень 2 или дочерние узлы. Ветвление может продолжаться на многие уровни, имея потенциал бесконечных уровней. Уровень 0 подобен текущему состоянию доски, а уровень 1 — это все возможные состояния досок в зависимости от следующего хода.

Таким образом, если Игрок 2 сделал ход, мы можем считать, что корневой узел — это текущее состояние доски, ожидающее хода Игрока 1. Узлы уровня 1 содержат все возможные ходы для игрока 1, а узлы уровня 2 содержат все возможные ходы для игрока 2 на основе каждого возможного хода игрока 1.

Рассмотрим пример, в котором есть четыре конечных состояния, и путь к ним лежит от корня к четырем листьям дерева. Значения четырех листьев: 3, 6 слева и 4, 7 справа. Настала очередь максимизатора/игрока 1 делать ход. Чтобы выполнить алгоритм, необходимо сделать предположения для каждого хода.

Если Игрок 1 решит пойти налево, Минимизатор/Игрок 2 должен выбрать наименьшее из 3 и 6, и поэтому он выберет 3. В то время как, если Игрок 1 выбирает право, Игрок 2 выберет 4, что является минимумом. из двух значений, 4 и 7. Итак, уровень 1 теперь имеет значения 3 и 4.

Поскольку сейчас очередь Игрока 1/Максимайзера, они должны выбрать максимальное количество узлов 1-го уровня. Таким образом, они выберут 3. Тогда оптимальный выбор — пойти налево.

Шаги для алгоритма минимум-максимум в ИИ можно сформулировать следующим образом:

1. Создайте все игровое дерево.
2. Оцените баллы для конечных узлов на основе функции оценки.
3. Возврат от листьев к корневым узлам:

Для Максимайзера выберите узел с максимальным количеством очков.

Для Minimizer выберите узел с минимальным счетом.

4. В корневом узле выберите узел с максимальным значением и выберите соответствующий ход.

Читайте также: Идеи проекта машинного обучения

Свойства алгоритма минимум-максимум в ИИ

• Алгоритм завершен, то есть в конечном дереве поиска решение обязательно будет найдено.
• Оптимально, если оба игрока играют оптимально.
• Из-за поиска в глубину (DFS) для дерева игры временная сложность алгоритма составляет O (b m ), где b — коэффициент ветвления, а m — максимальная глубина дерева.
• Как и DFS, пространственная сложность этого алгоритма равна O(bm).

Преимущества

• Проводится тщательная оценка пространства поиска.
• Принятие решений в ИИ легко возможно.
• С помощью этого алгоритма разрабатываются новые умные машины.

Ограничения

• Из-за огромного фактора ветвления процесс достижения цели идет медленнее.
• Оценка и поиск всех возможных узлов и ветвей ухудшает производительность и эффективность движка.
• У обоих игроков слишком много вариантов для выбора.
• Если есть ограничение по времени и пространству, невозможно исследовать все дерево.

Но с Alpha-Beta Pruning алгоритм можно улучшить.

Заключение

В этой статье объясняются все аспекты алгоритма min-max в ИИ. Сначала дается введение в теорию с примерами ее использования, после чего следует описание того, как алгоритм работает в игре.

Алгоритм разбит, чтобы объяснить, как принимается решение сделать оптимальный ход на основе ходов и встречных ходов игроков. Затем перечислены свойства алгоритма. Наконец, представлены преимущества и недостатки алгоритма.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с программой Executive PG IIIT-B и upGrad по машинному обучению и искусственному интеллекту , которая предназначена для работающих профессионалов и предлагает более 450 часов интенсивного обучения, более 30 тематических исследований и заданий, IIIT -B статус выпускника, 5+ практических практических проектов и помощь в трудоустройстве в ведущих фирмах.