Algorithme Min Max en IA : composants, propriétés, avantages et limites

L' algorithme min max en IA, populairement connu sous le nom de minimax, est un algorithme de retour en arrière utilisé dans la prise de décision, la théorie des jeux et l'intelligence artificielle (IA). Il est utilisé pour trouver le coup optimal pour un joueur, en supposant que l'adversaire joue également de manière optimale. L'ordinateur à deux joueurs ou les jeux en ligne populaires comme les échecs, le tic-tac-toe, les dames, le go, etc. utilisent cet algorithme.

Un algorithme de retour en arrière est utilisé pour trouver une solution aux problèmes de calcul de manière à ce qu'un candidat soit progressivement construit vers une solution, une étape à la fois. Et le candidat qui ne parvient pas à compléter une solution est immédiatement abandonné.

Comment ça marche?

Dans l' algorithme min max de l'IA, il y a deux joueurs, Maximiser et Minimiser. Ces deux joueurs jouent le jeu en essayant d'obtenir le score le plus élevé possible ou le bénéfice maximum tandis que l'adversaire essaie d'obtenir le score le plus bas ou le bénéfice minimum.

Chaque plateau de jeu a un score d'évaluation qui lui est attribué, de sorte que le Maximiseur sélectionnera la valeur maximisée, et le Minimiseur sélectionnera la valeur minimisée avec des mouvements de compteur. Si le Maximiser a le dessus, alors le score du tableau sera une valeur positive, et si le Minimiseur a le dessus, alors le score du tableau sera une valeur négative.

Ceci est basé sur le concept de jeu à somme nulle où le score total d'utilité est divisé entre les deux joueurs. Ainsi, une augmentation du score d'un joueur entraîne une diminution du score du joueur adverse, ce qui rend le score total toujours nul. Donc, pour qu'un joueur gagne, l'autre doit perdre.

Rejoignez les cours Machine Learning Certification & AI en ligne des meilleures universités du monde. Gagnez des Masters, Executive PGP ou ACP pour accélérer votre carrière.

Décomposer l'algorithme min max en IA

L'arborescence complète du jeu est explorée avec un algorithme de recherche en profondeur d'abord dans l'algorithme min max de l'IA. Il descend entièrement jusqu'au nœud terminal de l'arbre, puis revient en arrière dans l'arbre.

Le but est de trouver le meilleur coup possible pour un joueur. Cela peut être fait en choisissant le nœud avec le meilleur score d'évaluation. Le meilleur choix sera fait après avoir évalué tous les coups potentiels de l'adversaire. L'algorithme anticipe toutes les valeurs possibles jusqu'à la fin et prend une décision pour le joueur.

La source

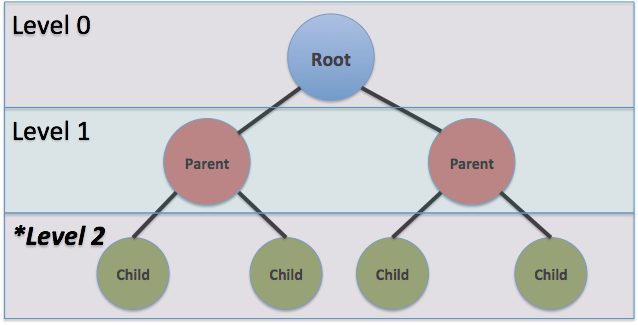
L'arbre de jeu ci-dessus est une structure de données imbriquée qui est utilisée pour évaluer les mouvements. Ici, le nœud racine est le niveau 0, qui se ramifie en niveau 1 ou nœuds parents, qui se ramifient ensuite en niveau 2 ou nœuds enfants. La ramification peut continuer à plusieurs niveaux, ayant le potentiel de niveaux infinis. Le niveau 0 correspond à l'état actuel du plateau, tandis que le niveau 1 correspond à tous les états possibles des plateaux en fonction du prochain coup.

Ainsi, si le joueur 2 a joué un coup, nous pouvons supposer que le nœud racine est l'état actuel du plateau, attendant le coup du joueur 1. Les nœuds de niveau 1 contiennent tous les mouvements possibles pour le joueur 1, et les nœuds de niveau 2 contiennent tous les mouvements possibles pour le joueur 2 en fonction de chaque mouvement possible du joueur 1.

Prenons un exemple où il y a quatre états finaux et le chemin pour les atteindre va de la racine aux quatre feuilles d'un arbre. Les valeurs des quatre feuilles sont 3, 6 à gauche et 4, 7 à droite. C'est au tour du Maximiseur/Joueur 1 de jouer. Pour exécuter l'algorithme, des hypothèses pour chaque mouvement doivent être faites.

Si le joueur 1 choisit d'aller à gauche, le minimiseur/joueur 2 doit choisir le moins entre 3 et 6, et il choisira donc 3. Alors que si le joueur 1 choisit à droite, le joueur 2 choisira 4, ce qui est le minimum. des deux valeurs, 4 et 7. Ainsi, le niveau 1 a maintenant les valeurs 3 et 4.

Puisque c'est au tour du joueur 1/maximiseur, il doit choisir le maximum de nœuds de niveau 1. Ainsi, ils choisiront 3. Ensuite, le choix optimal est d'aller à gauche.

Les étapes de l' algorithme min max dans AI peuvent être énoncées comme suit :

1. Créez l'arbre de jeu complet.
2. Évaluez les scores des nœuds terminaux en fonction de la fonction d'évaluation.
3. Revenir en arrière de la feuille aux nœuds racine :

Pour Maximizer, choisissez le nœud avec le score maximum.

Pour Minimizer, choisissez le nœud avec le score minimum.

4. Au nœud racine, choisissez le nœud avec la valeur maximale et sélectionnez le mouvement respectif.

Lisez aussi : Idées de projets d'apprentissage automatique

Propriétés de l'algorithme min max en IA

• L'algorithme est complet, ce qui signifie que dans un arbre de recherche fini, une solution sera certainement trouvée.
• Il est optimal si les deux joueurs jouent de manière optimale.
• En raison de la recherche en profondeur d'abord (DFS) pour l'arbre de jeu, la complexité temporelle de l'algorithme est O(b m ), où b est le facteur de branchement et m est la profondeur maximale de l'arbre.
• Comme DFS, la complexité spatiale de cet algorithme est O(bm).

Avantages

• Une évaluation approfondie de l'espace de recherche est effectuée.
• La prise de décision en IA est facilement possible.
• De nouvelles machines intelligentes sont développées avec cet algorithme.

Limites

• En raison de l'énorme facteur de ramification, le processus pour atteindre l'objectif est plus lent.
• L'évaluation et la recherche de tous les nœuds et branches possibles dégradent les performances et l'efficacité du moteur.
• Les deux joueurs ont trop de choix pour décider.
• S'il y a une restriction de temps et d'espace, il n'est pas possible d'explorer l'arbre entier.

Mais avec Alpha-Beta Pruning, l'algorithme peut être amélioré.

Conclusion

Cet article explique tous les aspects de l' algorithme min-max en IA. Tout d'abord, une introduction de la théorie est fournie avec des exemples d'utilisation, après quoi il y a une description de la façon dont l'algorithme fonctionne dans un jeu.

L'algorithme est décomposé pour expliquer comment une décision de faire un mouvement optimal est prise en fonction des mouvements et des contre-mouvements des joueurs. Les propriétés de l'algorithme sont ensuite listées. Enfin, les avantages et les inconvénients de l'algorithme sont fournis.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le programme Executive PG d'IIIT-B & upGrad en apprentissage automatique et IA , conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT -B Statut d'anciens élèves, 5+ projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.