人工智能中的最小最大算法：组件、属性、优势和限制

AI 中的min max 算法，俗称 minimax，是一种用于决策制定、博弈论和人工智能 (AI) 的回溯算法。 它用于为玩家找到最佳移动，假设对手也在最佳发挥。 国际象棋、井字游戏、跳棋、围棋等流行的两人计算机或在线游戏都使用此算法。

回溯算法用于找到计算问题的解决方案，使得候选者逐步朝着解决方案构建，一次一步。 未能完成解决方案的候选人将立即被放弃。

它是如何工作的？

在AI 中的 min max 算法中，有两个玩家，Maximiser 和 Minimiser。 这两个玩家在玩游戏时都试图获得尽可能高的分数或最大的利益，而对手试图获得最低的分数或最小的利益。

每个游戏板都有一个分配给它的评估分数，因此 Maximiser 将选择最大值，而 Minimiser 将通过反动作选择最小值。 如果 Maximiser 占上风，则棋盘得分为正值，如果 Minimiser 占上风，则棋盘得分为负值。

这是基于零和游戏的概念，其中总效用得分在两个玩家之间分配。 因此，一个玩家得分的增加会导致对手玩家得分的减少，从而使总得分始终为零。 因此，要让一名球员获胜，另一名球员必须输球。

加入来自世界顶级大学的在线机器学习认证和 AI 课程。 获得 Masters、Executive PGP 或 ACP 以加快您的职业生涯。

分解 AI 中的 min max 算法

在 AI 的 min max 算法中使用深度优先搜索算法探索完整的博弈树。 它完全下到树的终端节点，然后回溯到树。

目标是为玩家找到可能的最佳移动。 这可以通过选择具有最佳评估分数的节点来完成。 在评估对手的所有潜在动作后，将做出最佳选择。 该算法会提前查看所有可能的值，直到最后并为玩家做出决定。

资源

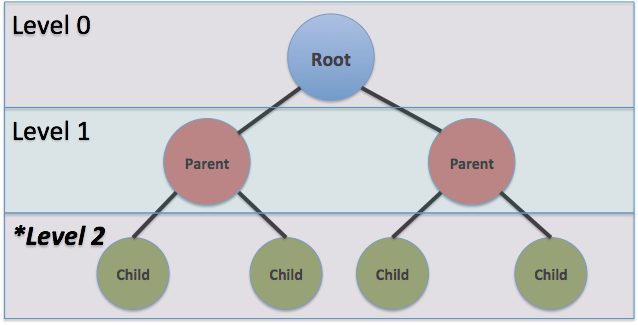
上面的博弈树是一个嵌套数据结构，用于评估移动。 这里的根节点是 0 级，它分支到 1 级或父节点，进一步分支到 2 级或子节点。 分支可以持续到多个层次，具有无限层次的潜力。 级别 0 就像棋盘的当前状态，而级别 1 是棋盘的所有可能状态，具体取决于下一步。

因此，如果玩家 2 已经移动，我们可以假设根节点是棋盘的当前状态，等待玩家 1 的移动。 级别 1 节点包含玩家 1 的所有可能移动，级别 2 节点包含基于玩家 1 的每个可能移动的玩家 2 的所有可能移动。

考虑一个示例，其中有四个最终状态，到达这些状态的路径是从树的根到四个叶子。 四个叶子的值分别是左边的3、6和右边的4、7。 轮到 Maximiser/Player 1 采取行动了。 为了运行算法，必须对每一步做出假设。

如果玩家 1 选择向左走，那么 Minimiser/玩家 2 必须在 3 和 6 之间选择最小的，所以他们会选择 3。而如果玩家 1 选择向右，玩家 2 将选择 4，这是最小的4 和 7 这两个值中的一个。因此，级别 1 现在具有值 3 和 4。

由于轮到玩家 1/Maximiser，他们必须选择 1 级节点的最大值。 因此，他们会选择 3。那么最优选择是向左走。

AI中的min max算法的步骤可以表述如下：

1. 创建整个游戏树。
2. 根据评估函数评估叶节点的分数。
3. 从叶子节点回溯到根节点：

对于 Maximizer，选择得分最高的节点。

对于 Minimizer，选择得分最低的节点。

4. 在根节点，选择具有最大值的节点并选择相应的移动。

另请阅读：机器学习项目理念

AI 中 min max 算法的属性

• 该算法是完整的，意味着在有限的搜索树中，一定会找到解决方案。
• 如果两个玩家都在最佳状态下玩，那是最佳的。
• 由于博弈树的深度优先搜索 (DFS)，算法的时间复杂度为 O(b m )，其中 b 是分支因子，m 是树的最大深度。
• 与 DFS 一样，该算法的空间复杂度为 O(bm)。

优点

• 对搜索空间进行全面评估。
• 人工智能中的决策很容易实现。
• 使用这种算法开发了新的智能机器。

限制

• 由于分支因子巨大，达到目标的过程较慢。
• 评估和搜索所有可能的节点和分支会降低引擎的性能和效率。
• 两名球员都有太多的选择需要决定。
• 如果有时间和空间的限制，是不可能探索整棵树的。

但是使用 Alpha-Beta Pruning，可以改进算法。

结论

本文解释了AI 中 min-max 算法的所有方面。 首先，介绍了该理论，并提供了使用位置的示例，然后描述了该算法在游戏中的工作原理。

该算法被分解以解释如何根据玩家的移动和反移动来做出做出最佳移动的决定。 然后列出算法的属性。 最后，给出了该算法的优缺点。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和 AI 执行 PG 计划，该计划专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT -B 校友身份，5 个以上实用的实践顶点项目和顶级公司的工作协助。