AIの最小最大アルゴリズム：コンポーネント、プロパティ、利点、制限

一般にミニマックスとして知られているAIのミニマックスアルゴリズムは、意思決定、ゲーム理論、人工知能（AI）で使用されるバックトラッキングアルゴリズムです。 対戦相手も最適にプレーしていると仮定して、プレーヤーに最適な動きを見つけるために使用されます。 人気のある2人用コンピューター、またはチェス、三目並べ、チェッカー、囲碁などのオンラインゲームがこのアルゴリズムを使用します。

バックトラッキングアルゴリズムを使用して、計算問題の解決策を見つけ、候補者が一度に1ステップずつ解決策に向かって段階的に構築されるようにします。 そして、解決策を完了できなかった候補者はすぐに放棄されます。

それはどのように機能しますか？

AIの最小最大アルゴリズムには、MaximiserとMinimiserの2つのプレーヤーがあります。 対戦相手が最低のスコアまたは最小の利益を得ようとしている間、これらのプレーヤーは両方とも、可能な限り最高のスコアまたは最大の利益を得ようとするときにゲームをプレイします。

すべてのゲームボードには評価スコアが割り当てられているため、マキシマイザーは最大化された値を選択し、ミニマイザーはカウンターの動きで最小化された値を選択します。 Maximiserが優勢である場合、ボードスコアは正の値になり、Minimiserが優勢である場合、ボードスコアは負の値になります。

これは、合計ユーティリティスコアが2人のプレーヤー間で分割されるゼロサムゲームの概念に基づいています。 したがって、1人のプレーヤーのスコアが増加すると、対戦相手のプレーヤーのスコアが減少し、合計スコアは常にゼロになります。 したがって、一方のプレーヤーが勝つには、もう一方のプレーヤーが負ける必要があります。

世界のトップ大学からオンラインで機械学習認定とAIコースに参加してください。 マスター、エグゼクティブPGP、またはACPを獲得して、キャリアを早急に進めましょう。

AIの最小最大アルゴリズムの内訳

完全なゲームツリーは、AIの最小最大アルゴリズムの深さ優先探索アルゴリズムで探索されます。 ツリーのターミナルノードまで完全に進み、ツリーをバックトラックします。

目標は、プレーヤーにとって可能な限り最良の動きを見つけることです。 これは、評価スコアが最も高いノードを選択することで実行できます。 対戦相手のすべての潜在的な動きを評価した後、最良の選択が行われます。 アルゴリズムは、可能なすべての値を最後まで先読みし、プレーヤーの決定を下します。

ソース

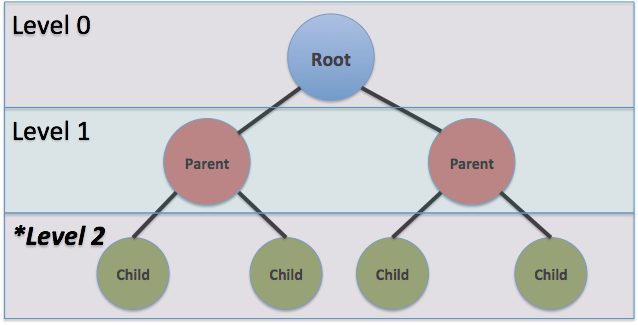
上記のゲームツリーは、動きを評価するために使用されるネストされたデータ構造です。 ここで、ルートノードはレベル0であり、レベル1または親ノードに分岐し、さらにレベル2または子ノードに分岐します。 分岐は多くのレベルに続く可能性があり、無限のレベルの可能性があります。 レベル0はボードの現在の状態に似ていますが、レベル1は、次の動きに応じてボードのすべての可能な状態です。

したがって、プレーヤー2が移動した場合、ルートノードはボードの現在の状態であり、プレーヤー1の移動を待機していると見なすことができます。 レベル1ノードには、プレーヤー1のすべての可能な動きが含まれ、レベル2ノードには、プレーヤー1のそれぞれの可能な動きに基づいて、プレーヤー2のすべての可能な動きが含まれます。

4つの最終状態があり、これらに到達するためのパスが木の根から4枚の葉までである例を考えてみます。 4枚の葉の値は、左側が3、6、右側が4、7です。 Maximiser /Player1が動き出す番です。 アルゴリズムを実行するには、各移動の仮定を行う必要があります。

プレーヤー1が左に行くことを選択した場合、ミニマイザー/プレーヤー2は3から6の間で最小を選択する必要があるため、3を選択します。一方、プレーヤー1が右を選択した場合、プレーヤー2は最小の4を選択します。したがって、レベル1の値は3と4になります。

プレイヤー1/マキシマイザーの番なので、レベル1ノードの最大数を選択する必要があります。 したがって、彼らは3を選択します。次に、最適な選択は左に行くことです。

AIの最小最大アルゴリズムの手順は次のように記述できます。

1. ゲームツリー全体を作成します。
2. 評価関数に基づいて、リーフノードのスコアを評価します。
3. リーフからルートノードへのバックトラック：

Maximizerの場合、スコアが最大のノードを選択します。

Minimizerの場合、スコアが最小のノードを選択します。

4. ルートノードで、最大値のノードを選択し、それぞれの移動を選択します。

また読む：機械学習プロジェクトのアイデア

AIの最小最大アルゴリズムのプロパティ

• アルゴリズムは完全です。つまり、有限の探索木では、解決策が確実に見つかります。
• 両方のプレイヤーが最適にプレイしている場合に最適です。
• ゲームツリーの深さ優先探索（DFS）により、アルゴリズムの時間計算量はO（b m ）です。ここで、bは分岐係数、mはツリーの最大深度です。
• DFSと同様に、このアルゴリズムのスペースの複雑さはO（bm）です。

利点

• サーチスペースの徹底的な評価が実行されます。
• AIでの意思決定は簡単に可能です。
• このアルゴリズムを使用して、新しくスマートなマシンが開発されています。

制限事項

• 分岐係数が大きいため、目標に到達するプロセスは遅くなります。
• 考えられるすべてのノードとブランチを評価および検索すると、エンジンのパフォーマンスと効率が低下します。
• どちらのプレイヤーも選択肢が多すぎて決定できません。
• 時間と空間に制限がある場合、ツリー全体を探索することはできません。

しかし、アルファベータプルーニングを使用すると、アルゴリズムを改善できます。

結論

この記事では、AIの最小-最大アルゴリズムのすべての側面について説明します。 最初に、理論の紹介がそれが使用される場所の例で提供され、その後、アルゴリズムがゲームでどのように機能するかについての説明があります。

アルゴリズムは、プレーヤーの動きとカウンターの動きに基づいて最適な動きをする決定がどのように行われるかを説明するために分解されます。 次に、アルゴリズムのプロパティが一覧表示されます。 最後に、アルゴリズムの長所と短所を示します。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。このプログラムは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIITを提供しています。 -B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との雇用支援。