Implementare Java Merge Sort algoritm? Explicație detaliată și tutorial complet
Publicat: 2021-01-20
Pe Crunchify, am scris până acum 500+ Java and Spring MVC . Nu m-a plictisit niciodată să învăț lucruri noi. Îmi place să învăț lucruri noi în fiecare zi și cred că este la fel și pentru cititorii mei :).
După cum probabil ați văzut înainte Algoritmul de sortare cu bule, algoritmul de sortare de selecție și algoritmul de sortare prin inserție este foarte popular printre diverse interviuri.
În acest tutorial, vom trece peste Merge Sort Algorithm .
Algoritmul de sortare fuzionare este foarte simplu. Împărțiți o matrice în jumătate când ajunge la un singur nivel, apoi sortați-o. Următorul pas este să-l îmbinați în succesiune. Practic, este abordarea divide and conquer .
Iată o explicație simplă despre sortarea de îmbinare despre cum se va împărți și îmbina elementele.
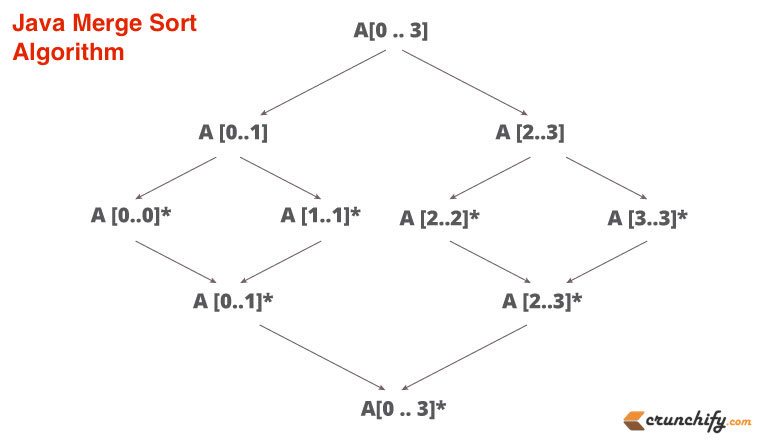
Să răspundem astăzi la toate întrebările de mai jos în acest tutorial:
- Ce este algoritmul de sortare de îmbinare?
- Ce este implementarea fuziunii?
- Mergesort în Java – Tutorial
- merge sort codul java
Vom efectua pașii de mai jos:
- Creați
crunchifyArraycu dimensiunea 10 - Completați 10 numere întregi aleatorii în matrice
- Imprimați matricea inițială
- Efectuați sortarea prin îmbinare
- Imprimați matricea finală după sortarea îmbinării
Iată un cod Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
package crunchify . com . tutorial ; import java . util . * ; /** * @author Crunchify.com Merge Sort Algorithm in Java * */ public class CrunchifyMergeSortAlgorithm { public static Integer [ ] crunchifyArray = new Integer [ 10 ] ; ; public static int iteration = 1 ; // Divide and Merge public static void crunchifyMergeSort ( Integer [ ] crunchifyArray ) { Integer [ ] tempArray = new Integer [ crunchifyArray . length ] ; // recursively perform merge sort crunchifyMergeSort ( crunchifyArray , tempArray , 0 , crunchifyArray . length - 1 ) ; } // Idea is simple: // First divide whole array into 2 part // Divide each array into another 2 part // Once it reaches to only 1 elements in each side tree, just sort it // Merge backward the same way to get complete sorted array private static void crunchifyMergeSort ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int myLeft , int myRight ) { if ( myLeft < myRight ) { int center = ( myLeft + myRight ) / 2 ; crunchifyMergeSort ( crunchifyArray , tempArray , myLeft , center ) ; crunchifyMergeSort ( crunchifyArray , tempArray , center + 1 , myRight ) ; crunchifyMerge ( crunchifyArray , tempArray , myLeft , center + 1 , myRight ) ; } } // Merge Sort Algorithm private static void crunchifyMerge ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int left , int myRight , int rightMost ) { int leftEnd = myRight - 1 ; int k = left ; int num = rightMost - left + 1 ; while ( left < = leftEnd && myRight <= rightMost) if (crunchifyArray[left].compareTo(crunchifyArray[myRight]) <= 0) tempArray[k++] = crunchifyArray[left++]; else tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ; while ( left < = leftEnd ) tempArray [ k ++ ] = crunchifyArray [ left ++ ] ; while ( myRight < = rightMost ) tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ; for ( int i = 0 ; i < num ; i ++ , rightMost -- ) crunchifyArray [ rightMost ] = tempArray [ rightMost ] ; System . out . print ( "Iteration # " + iteration + " ===> " ) ; crunchifyPrint ( ) ; iteration ++ ; } // Get Random Integer in Java public static Integer getRandomIntegers ( ) { Random crunchifyRandom = new Random ( ) ; int myNumber = crunchifyRandom . nextInt ( 150 ) ; return myNumber ; } // Simply Print Arrays public static void crunchifyPrint ( ) { for ( int n : crunchifyArray ) { System . out . print ( " " + n + " " ) ; } System . out . print ( "\n" ) ; } // Main Method public static void main ( String [ ] args ) { for ( int i = 0 ; i < crunchifyArray . length ; i ++ ) { crunchifyArray [ i ] = getRandomIntegers ( ) ; } System . out . print ( "Here is our initial array: " ) ; crunchifyPrint ( ) ; System . out . println ( ) ; // Perform actual sorting crunchifyMergeSort ( crunchifyArray ) ; System . out . println ( ) ; System . out . print ( "Here is an array after Merge Sort: " ) ; crunchifyPrint ( ) ; } } |
Ieșire consola Eclipse:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Here is our initial array : 45 53 10 50 48 8 106 77 44 108 Iteration # 1 ===> 45 53 10 50 48 8 106 77 44 108 Iteration # 2 ===> 10 45 53 50 48 8 106 77 44 108 Iteration # 3 ===> 10 45 53 48 50 8 106 77 44 108 Iteration # 4 ===> 10 45 48 50 53 8 106 77 44 108 Iteration # 5 ===> 10 45 48 50 53 8 106 77 44 108 Iteration # 6 ===> 10 45 48 50 53 8 77 106 44 108 Iteration # 7 ===> 10 45 48 50 53 8 77 106 44 108 Iteration # 8 ===> 10 45 48 50 53 8 44 77 106 108 Iteration # 9 ===> 8 10 44 45 48 50 53 77 106 108 Here is an array after Merge Sort : 8 10 44 45 48 50 53 77 106 108 |
Încercați programul de depanare cu atenție pentru a înțelege două metode crunchifyMergeSort și crunchifyMerge . Anunțați-mă dacă aveți întrebări sau probleme la rularea codului de mai sus.

Notație O mare / Ce este o complexitate a algorilor de sortare fuzionare?
-
n*log(n)
Merge Sort Cel mai bun caz Complexitatea scenariului?
-
O(n)în cazul intrării deja sortate
