Implementacja algorytmu sortowania przez scalanie w języku Java? Szczegółowe wyjaśnienie i kompletny samouczek

Opublikowany: 2021-01-20
Implementacja algorytmu sortowania przez scalanie w języku Java? Szczegółowe wyjaśnienie i kompletny samouczek

W Crunchify napisaliśmy do tej pory ponad 500+ Java and Spring MVC . Uczenie się nowych rzeczy nigdy mnie nie nudziło. Lubię uczyć się nowych rzeczy każdego dnia i wierzę, że to samo dotyczy moich czytelników :).

Jak być może widzieliście wcześniej, algorytmy sortowania bąbelkowego, algorytmy sortowania przez selekcję i algorytmy przez wstawianie są bardzo popularne wśród różnych wywiadów.

W tym samouczku omówimy Merge Sort Algorithm .

Algorytm sortowania przez scalanie jest bardzo prosty. Podziel tablicę na pół, gdy osiągnie tylko jeden poziom, a następnie posortuj ją. Następnym krokiem jest połączenie go w kolejności. Zasadniczo jest to podejście divide and conquer .

Oto proste wyjaśnienie dotyczące sortowania przez scalanie, w jaki sposób podzielić i scalić elementy.

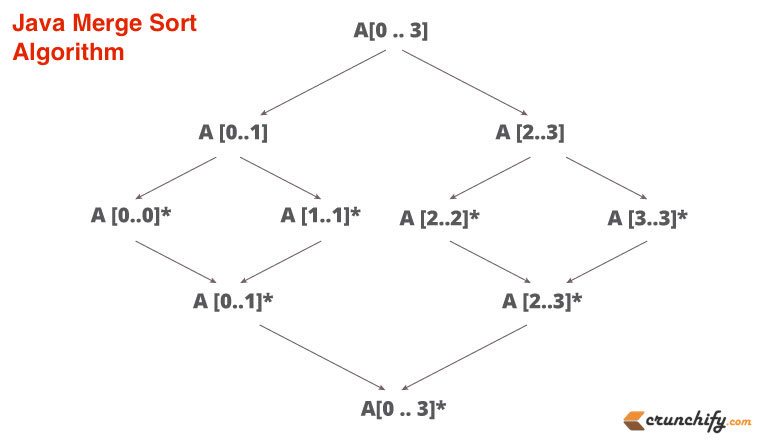
Odpowiedzmy dzisiaj na wszystkie poniższe pytania w tym samouczku:

  • Jaki jest algorytm sortowania przez scalanie?
  • Jak wygląda realizacja fuzji?
  • Mergesort w Javie – samouczek
  • scalanie sortowania kodu java

Wykonamy poniższe kroki:

  1. Utwórz crunchifyArray o rozmiarze 10
  2. Wypełnij 10 losowych liczb całkowitych do tablicy
  3. Wydrukuj początkową tablicę
  4. Wykonaj sortowanie scalające
  5. Wydrukuj ostateczną tablicę po sortowaniu przez scalanie

Oto kod Java:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
package crunchify . com . tutorial ;
 
import java . util . * ;
 
/**
* @author Crunchify.com Merge Sort Algorithm in Java
*
*/
 
public class CrunchifyMergeSortAlgorithm {
public static Integer [ ] crunchifyArray = new Integer [ 10 ] ; ;
public static int iteration = 1 ;
 
// Divide and Merge
public static void crunchifyMergeSort ( Integer [ ] crunchifyArray ) {
Integer [ ] tempArray = new Integer [ crunchifyArray . length ] ;
 
// recursively perform merge sort
crunchifyMergeSort ( crunchifyArray , tempArray , 0 , crunchifyArray . length - 1 ) ;
 
}
 
// Idea is simple:
// First divide whole array into 2 part
// Divide each array into another 2 part
// Once it reaches to only 1 elements in each side tree, just sort it
// Merge backward the same way to get complete sorted array
private static void crunchifyMergeSort ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int myLeft , int myRight ) {
 
if ( myLeft < myRight ) {
int center = ( myLeft + myRight ) / 2 ;
crunchifyMergeSort ( crunchifyArray , tempArray , myLeft , center ) ;
crunchifyMergeSort ( crunchifyArray , tempArray , center + 1 , myRight ) ;
crunchifyMerge ( crunchifyArray , tempArray , myLeft , center + 1 , myRight ) ;
}
}
 
// Merge Sort Algorithm
private static void crunchifyMerge ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int left , int myRight ,
int rightMost ) {
int leftEnd = myRight - 1 ;
int k = left ;
int num = rightMost - left + 1 ;
 
while ( left < = leftEnd && myRight <= rightMost)
if (crunchifyArray[left].compareTo(crunchifyArray[myRight]) <= 0)
tempArray[k++] = crunchifyArray[left++];
else
tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ;
 
while ( left < = leftEnd )
tempArray [ k ++ ] = crunchifyArray [ left ++ ] ;
 
while ( myRight < = rightMost )
tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ;
 
for ( int i = 0 ; i < num ; i ++ , rightMost -- )
crunchifyArray [ rightMost ] = tempArray [ rightMost ] ;
 
System . out . print ( "Iteration # " + iteration + " ===> " ) ;
crunchifyPrint ( ) ;
iteration ++ ;
 
}
 
// Get Random Integer in Java
public static Integer getRandomIntegers ( ) {
 
Random crunchifyRandom = new Random ( ) ;
int myNumber = crunchifyRandom . nextInt ( 150 ) ;
return myNumber ;
}
 
// Simply Print Arrays
public static void crunchifyPrint ( ) {
for ( int n : crunchifyArray ) {
System . out . print ( " " + n + "  " ) ;
}
System . out . print ( "\n" ) ;
}
 
// Main Method
public static void main ( String [ ] args ) {
 
for ( int i = 0 ; i < crunchifyArray . length ; i ++ ) {
crunchifyArray [ i ] = getRandomIntegers ( ) ;
}
 
System . out . print ( "Here is our initial array: " ) ;
crunchifyPrint ( ) ;
System . out . println ( ) ;
 
// Perform actual sorting
crunchifyMergeSort ( crunchifyArray ) ;
 
System . out . println ( ) ;
System . out . print ( "Here is an array after Merge Sort: " ) ;
crunchifyPrint ( ) ;
}
}

Dane wyjściowe konsoli Eclipse:

1
2
3
4
5
6
7
8
9
10
11
12
13
Here is our initial array :    45    53    10    50    48    8    106    77    44    108   
 
Iteration # 1 ===>  45   53   10   50   48   8   106   77   44   108  
Iteration # 2 ===>  10   45   53   50   48   8   106   77   44   108  
Iteration # 3 ===>  10   45   53   48   50   8   106   77   44   108  
Iteration # 4 ===>  10   45   48   50   53   8   106   77   44   108  
Iteration # 5 ===>  10   45   48   50   53   8   106   77   44   108  
Iteration # 6 ===>  10   45   48   50   53   8   77   106   44   108  
Iteration # 7 ===>  10   45   48   50   53   8   77   106   44   108  
Iteration # 8 ===>  10   45   48   50   53   8   44   77   106   108  
Iteration # 9 ===>  8   10   44   45   48   50   53   77   106   108  
 
Here is an array after Merge Sort :    8    10    44    45    48    50    53    77    106    108   

Wypróbuj dokładnie program do debugowania, aby zrozumieć dwie metody crunchifyMergeSort i crunchifyMerge . Daj mi znać, jeśli masz jakiekolwiek pytania lub problemy z uruchomieniem powyższego kodu.

Notacja Big O / Co to jest złożoność algorytmu sortowania przez scalanie?

  • n*log(n)

Złożoność scenariusza scalania sortowania według najlepszego scenariusza?

  • O(n) w przypadku już posortowanych danych wejściowych