• Startseite
  • Artikel
  • Allgemein
  • Implementierung des Java-Merge-Sortieralgorithmus? Ausführliche Erklärung und vollständiges Tutorial

Implementierung des Java-Merge-Sortieralgorithmus? Ausführliche Erklärung und vollständiges Tutorial

Veröffentlicht: 2021-01-20
Implementierung des Java-Merge-Sortieralgorithmus? Ausführliche Erklärung und vollständiges Tutorial

Auf Crunchify haben wir bisher über 500 Tutorials 500+ Java and Spring MVC -Technologie geschrieben. Neues zu lernen hat mich nie gelangweilt. Ich lerne gerne jeden Tag neue Sachen und ich glaube, dass es meinen Lesern genauso geht :).

Wie Sie vielleicht schon gesehen haben, sind der Bubble Sort-Algorithmus, der Selection Sort-Algorithmus und der Insertion Sort-Algorithmus bei verschiedenen Interviews sehr beliebt.

In diesem Tutorial gehen wir auf Merge Sort Algorithm ein.

Der Merge-Sortalgorithmus ist sehr einfach. Teilen Sie ein Array in zwei Hälften, wenn es nur eine Ebene erreicht, und sortieren Sie es dann. Der nächste Schritt besteht darin, sie der Reihe nach zusammenzuführen. Im Grunde ist es ein Teile- divide and conquer -Ansatz.

Hier ist eine einfache Erklärung zum Zusammenführen von Sortieren, wie Elemente geteilt und zusammengeführt werden.

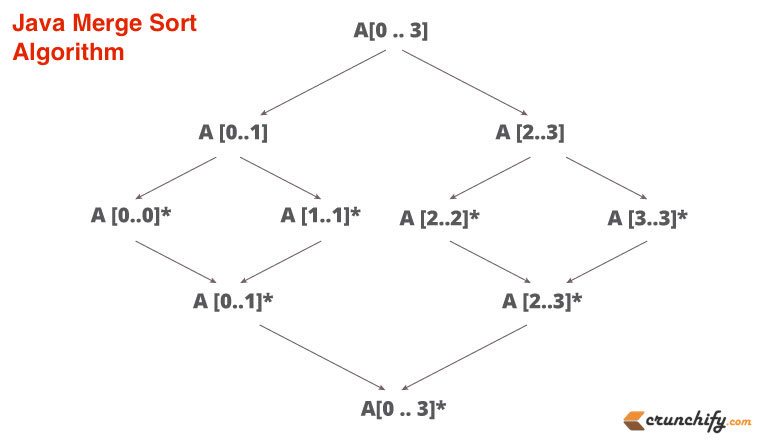
Lassen Sie uns heute in diesem Tutorial alle folgenden Fragen beantworten:

  • Was ist der Merge-Sort-Algorithmus?
  • Was ist die Implementierung von Merge?
  • Mergesort in Java – Tutorial
  • Sortieren von Java-Code zusammenführen

Wir werden die folgenden Schritte ausführen:

  1. Erstellen Sie crunchifyArray mit der Größe 10
  2. Füllen Sie 10 zufällige ganze Zahlen in das Array
  3. Anfangs-Array drucken
  4. Mischsortierung durchführen
  5. Endgültiges Array nach Zusammenführungssortierung drucken

Hier ist ein Java-Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
package crunchify . com . tutorial ;
 
import java . util . * ;
 
/**
* @author Crunchify.com Merge Sort Algorithm in Java
*
*/
 
public class CrunchifyMergeSortAlgorithm {
public static Integer [ ] crunchifyArray = new Integer [ 10 ] ; ;
public static int iteration = 1 ;
 
// Divide and Merge
public static void crunchifyMergeSort ( Integer [ ] crunchifyArray ) {
Integer [ ] tempArray = new Integer [ crunchifyArray . length ] ;
 
// recursively perform merge sort
crunchifyMergeSort ( crunchifyArray , tempArray , 0 , crunchifyArray . length - 1 ) ;
 
}
 
// Idea is simple:
// First divide whole array into 2 part
// Divide each array into another 2 part
// Once it reaches to only 1 elements in each side tree, just sort it
// Merge backward the same way to get complete sorted array
private static void crunchifyMergeSort ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int myLeft , int myRight ) {
 
if ( myLeft < myRight ) {
int center = ( myLeft + myRight ) / 2 ;
crunchifyMergeSort ( crunchifyArray , tempArray , myLeft , center ) ;
crunchifyMergeSort ( crunchifyArray , tempArray , center + 1 , myRight ) ;
crunchifyMerge ( crunchifyArray , tempArray , myLeft , center + 1 , myRight ) ;
}
}
 
// Merge Sort Algorithm
private static void crunchifyMerge ( Integer [ ] crunchifyArray , Integer [ ] tempArray , int left , int myRight ,
int rightMost ) {
int leftEnd = myRight - 1 ;
int k = left ;
int num = rightMost - left + 1 ;
 
while ( left < = leftEnd && myRight <= rightMost)
if (crunchifyArray[left].compareTo(crunchifyArray[myRight]) <= 0)
tempArray[k++] = crunchifyArray[left++];
else
tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ;
 
while ( left < = leftEnd )
tempArray [ k ++ ] = crunchifyArray [ left ++ ] ;
 
while ( myRight < = rightMost )
tempArray [ k ++ ] = crunchifyArray [ myRight ++ ] ;
 
for ( int i = 0 ; i < num ; i ++ , rightMost -- )
crunchifyArray [ rightMost ] = tempArray [ rightMost ] ;
 
System . out . print ( "Iteration # " + iteration + " ===> " ) ;
crunchifyPrint ( ) ;
iteration ++ ;
 
}
 
// Get Random Integer in Java
public static Integer getRandomIntegers ( ) {
 
Random crunchifyRandom = new Random ( ) ;
int myNumber = crunchifyRandom . nextInt ( 150 ) ;
return myNumber ;
}
 
// Simply Print Arrays
public static void crunchifyPrint ( ) {
for ( int n : crunchifyArray ) {
System . out . print ( " " + n + "  " ) ;
}
System . out . print ( "\n" ) ;
}
 
// Main Method
public static void main ( String [ ] args ) {
 
for ( int i = 0 ; i < crunchifyArray . length ; i ++ ) {
crunchifyArray [ i ] = getRandomIntegers ( ) ;
}
 
System . out . print ( "Here is our initial array: " ) ;
crunchifyPrint ( ) ;
System . out . println ( ) ;
 
// Perform actual sorting
crunchifyMergeSort ( crunchifyArray ) ;
 
System . out . println ( ) ;
System . out . print ( "Here is an array after Merge Sort: " ) ;
crunchifyPrint ( ) ;
}
}

Ausgabe der Eclipse-Konsole:

1
2
3
4
5
6
7
8
9
10
11
12
13
Here is our initial array :    45    53    10    50    48    8    106    77    44    108   
 
Iteration # 1 ===>  45   53   10   50   48   8   106   77   44   108  
Iteration # 2 ===>  10   45   53   50   48   8   106   77   44   108  
Iteration # 3 ===>  10   45   53   48   50   8   106   77   44   108  
Iteration # 4 ===>  10   45   48   50   53   8   106   77   44   108  
Iteration # 5 ===>  10   45   48   50   53   8   106   77   44   108  
Iteration # 6 ===>  10   45   48   50   53   8   77   106   44   108  
Iteration # 7 ===>  10   45   48   50   53   8   77   106   44   108  
Iteration # 8 ===>  10   45   48   50   53   8   44   77   106   108  
Iteration # 9 ===>  8   10   44   45   48   50   53   77   106   108  
 
Here is an array after Merge Sort :    8    10    44    45    48    50    53    77    106    108   

Versuchen Sie das Debugging-Programm sorgfältig, um die beiden Methoden crunchifyMergeSort und crunchifyMerge zu verstehen. Lassen Sie mich wissen, wenn Sie Fragen oder Probleme beim Ausführen des obigen Codes haben.

Big-O-Notation / Was ist eine Merge-Sort-Algo-Komplexität?

  • n*log(n)

Zusammenführen Sortieren Best-Case-Szenario Komplexität?

  • O(n) bei bereits sortierter Eingabe