Régression linéaire bayésienne : qu'est-ce que c'est, la fonction et les applications réelles en 2022

Publié: 2021-01-08

Table des matières

Qu'est-ce qu'une régression linéaire ?

La régression linéaire tente de montrer le lien entre deux facteurs en ajustant une condition directe à l'information remarquée. Une variable est considérée comme une variable illustrative, et l'autre est considérée comme une variable nécessiteuse. Par exemple, un modélisateur doit relier de nombreuses personnes à leurs statues en utilisant un modèle de rechute simple.

Maintenant, la prochaine étape consiste à savoir ce qu'est l'équation linéaire bayésienne et comment elle peut être calculée pour obtenir le résultat souhaité.

Maintenant, qu'est-ce que l'équation linéaire bayésienne ?

Ainsi, lorsque nous parlons de méthodes de régression bayésienne, nous savons que c'est une méthode très puissante car elles nous fournissent la distribution complète sur les paramètres de régression. Afin de calculer des données inadéquates ou des données distribuées inégales, la régression linéaire bayésienne fournit un mécanisme naturel.

Vous pouvez placer un a priori sur les coefficients afin que si les données sont absentes, l'a priori puisse prendre la place des données. L'analyse statistique est effectuée dans les conditions de l'interface bayésienne dans la régression linéaire bayésienne des statistiques.

Nous utilisons une distribution de probabilité au lieu d'estimations ponctuelles pour concevoir une régression linéaire.

La sortie est obtenue à partir d'une distribution de probabilité, plutôt que des techniques de régression habituelles. L'objectif de la régression linéaire bayésienne est de trouver Postérieur au lieu des paramètres du modèle.

Les paramètres du modèle sont censés provenir d'une distribution.

L'expression postérieure est

Postérieure= (Probabilité*Avant)/Normalisation

L'équation ci-dessus est similaire au théorème de Bayes, qui est

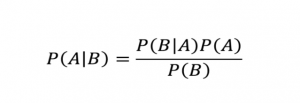
La source

Application réelle de la régression linéaire bayésienne

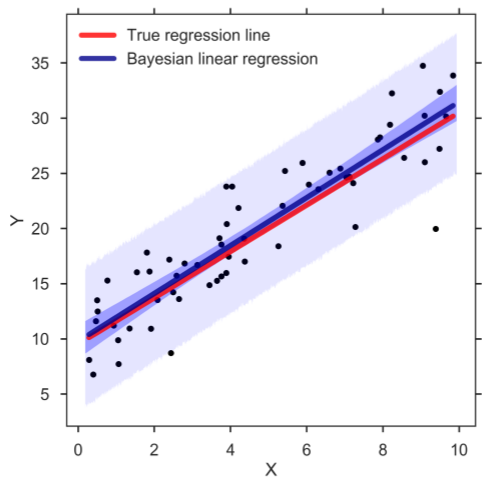
Selon les graphiques suivants, la régression linéaire et la régression bayésienne peuvent générer les mêmes prédictions.

La source

Dans le dernier graphique, nous pouvons supposer que si la distribution prédictive est à l'intérieur de la couleur épaisse, alors la densité de données est élevée et si elle est dans la zone rare, la densité peut être considérée comme faible.

Parlons de l'avantage de la régression bayésienne :

Avec l'aide du traitement bayésien, nous pouvons récupérer la variété complète des solutions inférentielles au lieu d'une estimation ponctuelle.
Cela fonctionne efficacement avec la petite taille de l'ensemble de données.
Il convient très bien à la forme d'apprentissage en ligne, alors que, sous la forme d'apprentissage par lots, nous avons l'ensemble des données.
C'est une approche très puissante et éprouvée.

Parlons maintenant de l'inconvénient de la régression linéaire bayésienne.

Cela ne fonctionne pas efficacement si le jeu de données contient une énorme quantité de données.
La conjecture du modèle peut prendre du temps.

Lire : Idées et sujets de projets linéaires

Conclusion

Ainsi, nous pouvons voir ce qu'est une puissante méthode de régression linéaire bayésienne. De nombreux avantages peuvent être tirés de la régression linéaire bayésienne et constituent l'un des mécanismes naturels pour calculer des données insuffisantes ou mal distribuées.

Un point de vue bayésien est une forme instinctive de voir le monde. À son homologue fréquent, l'inférence bayésienne peut embellir un substitut très pratique. Il est utilisé dans divers domaines tels que la science des données, l'apprentissage automatique et bien d'autres. Il aide à construire divers modèles à l'aide desquels nous pouvons résoudre de nombreux problèmes.

Si vous souhaitez en savoir plus sur les carrières dans l'apprentissage automatique et l'intelligence artificielle, consultez IIT Madras et la certification avancée d'upGrad en apprentissage automatique et cloud.

Qu'est-ce que l'inférence bayésienne ?

Les inférences bayésiennes sont un groupe d'opérations mathématiques basées sur le théorème de Bayes. C'est une méthode mathématique pour déterminer la probabilité conditionnelle. La possibilité qu'un résultat se produise en fonction de la probabilité qu'un résultat principal se produise est connue sous le nom de probabilité conditionnelle. Les professionnels peuvent utiliser le théorème de Bayes pour modifier les prévisions ou hypothèses précédentes. Il est utilisé en finance pour évaluer le risque de fournir de l'argent à des emprunteurs potentiels. En considérant la probabilité que chaque personne spécifique soit atteinte d'une maladie et la précision générale du test, le théorème de Bayes peut être utilisé pour évaluer la précision des résultats des tests médicaux.

En quoi la régression linéaire bayésienne est-elle différente de la régression linéaire ordinaire ?

La régression linéaire ordinaire est une méthode fréquentiste, ce qui implique qu'il existe suffisamment de mesures pour faire une déclaration valide. Les données sont complétées par des informations supplémentaires sous la forme d'une distribution de probabilité a priori dans la méthode bayésienne. La croyance a posteriori sur les paramètres est obtenue en combinant les connaissances antérieures sur les paramètres avec la fonction de vraisemblance des données en utilisant le théorème de Bayes. L'interprétation bayésienne de la régression linéaire et logistique utilise une analyse statistique dans le contexte de l'hypothèse bayésienne.

Comment fonctionne la régression linéaire bayésienne ?

Nous définissons la régression linéaire en utilisant des distributions de probabilité plutôt que des estimations ponctuelles dans une perspective bayésienne. La réponse, y, est censée être choisie à partir d'une distribution de probabilité plutôt que d'être évaluée comme un nombre unique. Le résultat, y, est produit par une distribution normale (gaussienne) avec une moyenne et une variance. Dans la régression linéaire, la moyenne est calculée en multipliant la matrice des poids par la matrice des prédicteurs. Puisqu'il s'agit d'une version multidimensionnelle du modèle, la variance est le carré de l'écart type multiplié par la matrice d'identité. L'objectif de la régression linéaire bayésienne est d'identifier la distribution a posteriori des paramètres du modèle, et non de trouver un résultat parfait particulier pour les paramètres du modèle.